Matematik Desteği
4. ve 5. Laboratuvarlarda ek matematik kavramları ve hesaplamalar öğretiliyor. Bu sayfa, öğrencilerin bu Laboratuvarlarda keşfettikleri matematiği desteklemek için öğretmenlere ilgili arka plan kaynakları sunmaktadır.
Sürüş Matematiği
4. Laboratuvardaki geçit törenini tamamlamak için öğrenciler, Kod Tabanı araçlarını düz bir geçit töreni güzergahı boyunca sürecekler. Öğrenciler, her iki tekerleği aynı anda hareket ettiren aktarma organları blokları kullanmak yerine, burada gösterildiği gibi VEXcode GO'daki [Spin for] bloklarını kullanarak tekerleklere bağlı motorları döndürecek ve robotu ileri doğru hareket ettirecekler. [Spin for] blokları parametre olarak 'dönüş' veya 'derece' kabul eder. Lab 4'te öğrenciler, robotlarını geçit töreni güzergahı boyunca götürmek için bu projeye girmeleri gereken tur sayısını hesaplayacaklar.
Robotunuzu belirli bir mesafe boyunca düz bir şekilde sürmek için gereken tekerlek dönüş sayısının nasıl hesaplanacağını öğrenmek için aşağıdaki videoyu izleyin.
Faydalı Referanslar:
Gri Tekerlekler için Terminoloji ve Değerler:
| Süre | Tanım | Görsel | Formül | Değer |
|---|---|---|---|---|
| Çap | Bir dairenin merkezi boyunca düz bir çizginin ölçülmesi |  |
d = 2 r | ~ 50,93 mm veya 2 inç |
| Çevre | Bir dairenin dış çevresindeki toplam mesafe |  |
C = π d | ~ 160 mm veya 6,25 inç |
Doğru Ölçme
Öğrenciler ölçerken, dikkatli ve hassas bir şekilde ölçmeleri için onlara rehberlik ettiğinizden emin olun. VEX GO Yazdırılabilir Cetvelöğrencilerin ölçüm yapması için veya sınıf cetvellerikullanabilirsiniz.
- Öğrencilere cetvelin sıfır noktasından ölçmeye başlamalarını hatırlatın. Ölçtükleri nesnenin bitiş noktasına dikkat edin. Ölçümlerini yanlış başlatmak veya sonlandırmak, hesaplamalarını ve robotlarının nihai hareketini etkileyecektir.
- Öğrencilerin doğru ölçüm yapabilmeleri için kullandıklarıüzerindeki işaretleri nasıl okuyacaklarını bildiklerinden emin olun. Kullandığınız cetvellerin hem emperyal hem de metrik birimleri varsa (VEX GO Yazdırılabilir Cetvel gibi), öğrencilerin sürekli olarak aynı ölçü birimlerini kullandığından emin olun.
Mavi renkle vurgulanan imparatorluk birimleri ve yeşil renkle vurgulanan metrik birimler ile - Öğrenciler ölçümlerini en yakın birime veya bir birimin kesirine yuvarlayabilirler. Yuvarlama, gerekirse hesaplamaları daha basit hale getirebilir; ancak ölçümleri daha az hassas hale de getirebilir. Örneğin, öğrencilere en yakın yarım inç veya santimetreye yuvarlamalarını söyleyebilirsiniz, ancak robotları başlangıçta amaçlanandan biraz daha uzağa hareket eder. Alternatif olarak, öğrencilerden bir inç veya milimetrenin en yakın noktasına kadar ölçüm yapmalarını isteyebilir ve robotlarının hedeflenen mesafeye daha yakın seyahat ettiğini görebilirsiniz.
- Öğrencilerin ölçme konusunda daha fazla pratiğe ihtiyaçları varsa, VEX GO Ölçüm Uygulama Etkinliği bireysel öğrencilerle veya gruplarla ya da tüm sınıf etkinliği olarak kullanabilirsiniz.
360° Dönmenin Matematiği
Lab 5 'teki geçit törenini tamamlamak için, öğrenciler Kod Tabanlarını bir geçiş güzergahı boyunca bir dönüşle sürecekler.
İleri sürmeyi ve ardından sağa dönmeyi gösteren oklu Kod Tabanı
Öğrenciler, robotu düz bir çizgi mesafesi kat edecek şekilde kodlama, robotu doğrusal olmayan bir mesafe veya bir dönüş yapacak şekilde kodlama hakkında öğrendiklerini geliştireceklerdir. Öğrenciler hala belirli bir mesafeyi kat etmek için gereken dönüş sayısını hesaplamaktadır, bu nedenle önceki Laboratuvardaki ile aynı formülü kullanacaklardır.
Öğrencilerinizle birlikte robotu 360° döndürmek için gereken tekerlek dönüş sayısını nasıl hesaplayacağınızı öğrenmek için aşağıdaki videoyu izleyin.
Faydalı Referanslar:
Kod Tabanı döndüğünde, tahrik tekerlekleri robotu döndürmek için zıt yönlerde hareket eder. Örneğin, robotu sağa çevirmek için sol tekerlek ileri doğru hareket ederken, sağ tekerlek geri yönde hareket edecektir.
Kod Tabanı için Terminoloji ve Değerler:
| Süre | Tanım | Görsel | Formül | Değer |
|---|---|---|---|---|
| Çap | Her tekerleğin merkezinden düz bir çizginin ölçülmesi (dingil mesafesi olarak da bilinir) |  |
d = 2 r | ~ 135 mm veya 5,3 inç |
| Çevre | 360 °' yi tamamlamak için tekerleklerin sürdüğü toplam mesafe |  |
C = π d | ~ 424 mm veya 16,7 inç |
Herhangi Bir Derecede Tornalama Matematiği
Robotun herhangi bir derece dönmesi için gereken tekerlek dönüş sayısını hesaplama hakkında daha fazla bilgi edinmek için bu videoyu izleyin.
Dereceye Dönüştürme
[Spin for] bloğu parametre olarak dönüşleri veya dereceleri kabul edecektir. Dereceleri kullanmak için, dönüş sayısını 360 ile çarpmanız yeterlidir. Bu örnekte robotun tam° dönebilmesi için motorların kaç derece dönmesi gerektiği gösterilmektedir. Bu projede motorların zıt yönlerde döndüğünü ve ilk bloğa 've bekleme' ifadesinin eklendiğini, böylece motorların aynı anda döndüğünü unutmayın. Bu, robotu istenen 360° için sağa döndürecektir. 
Yaygın Kavram Yanılgıları
Öğrencilerin ölçme ve sürüş ve dönme matematiği hakkında sahip olabilecekleri birkaç kavram yanılgısı vardır. Bunlar en yaygın olanlardan bazılarıdır ve öğrencilerinizle bunları nasıl ele alabileceğinize dair öneriler içerir.
| Durum | Kavram yanılgısı | Önerilen Düzeltme |
|---|---|---|
|
Öğretmen sınıfa, robotu 90° döndürmek için [Spin for] bloğuna ne girmemiz gerektiğini sorar. Öğrenci “90” yanıtını verir. |
Tekerleğin dönüş yapmak için sürdüğü derece cinsinden mesafe, dönüş açısına eşittir. Öğrenciler, tekerleğin sürmesi gereken mesafeyi hesaplamak için robotun dönüş çevresini kullanmıyor. |
Öğrencilere, robotun dönmesi için tekerleklerin dönüş çevresi boyunca sürmesi gerektiğini hatırlatın. (Bu resimde, yani bir sarı çizgiden diğerine kırmızı daire boyunca.)
Öğrencilerin tekerleğin belirli bir mesafe kat etmek için ne kadar döndüğünü görselleştirmelerine yardımcı olmak için tekerleği sadece 90° döndürün. |
|
Öğretmen sınıfa, robotun 30 cm ileri gitmesini sağlamak için [Spin for] bloğuna ne girmemiz gerektiğini sorar. Öğrenci “12” yanıtını verir. |
Tekerlek dönüş sayısı, istenen sürüş mesafesine eşittir. Öğrenci, istenen mesafeyi sürmek için tekerlek dönüş sayısını hesaplamak için tekerlek çevresini kullanmamaktadır. |
Öğrencilere robotun 1 tekerlek dönüşüyle ne kadar uzağa hareket ettiğini hatırlatın ve 12 inç sürmek için 12 dönüşün çok fazla veya çok az gibi görünüp görünmediğini sorun. Öğrencilerin bunu daha iyi görselleştirmelerine yardımcı olmak için, öğrencilere bu mesafenin ne kadar olduğunu göstermek için 12 tekerlek dönüşü boyunca bir cetvel boyunca bir tekerlek yuvarlayın.
Öğrencilere 1 tekerlek dönüşünün tekerlek çevresi olduğunu ve 12 inçin bu çevreye bölünmesi gerektiğini hatırlatın. |
| Öğrenci tekerleği ölçüyor, ancak tekerleğin her iki kenarı da cetvelin sıfır işaretinde değil. |
Cetvel sıfırdan değil 1 'den başlar. Öğrenci doğru ölçüm alabilmek için cetveli doğru kullanmıyor. |
Öğrencilere cetvelin ‘0‘ işaretinden başladığını ve o noktadan ölçüm yapmazlarsa ölçümlerinin yanlış olacağını hatırlatın. Cetvelin başlangıcını, çalışırken öğrenciler için ekstra bir görsel yardımcı olarak bant veya renkli bir işaretleyici ile işaretlemek isteyebilirsiniz. (Ölçme ile ekstra uygulama için, öğrenciler Uygulama Ölçme Etkinliğini tamamlayabilirler.) |
|
Bir öğrenci projesinin işe yaramadığını söylüyor. Öğretmen, doğru tekerlek dönüş sayısının [Spin for] bloğunda olduğunu fark eder, ancak parametre ‘degrees‘ olarak ayarlanır. |
Birimler veya parametreler değiştirilebilir. Öğrenciler projelerinde parametrelere/ölçü birimlerine katılmamaktadır. |
Öğrencilere hangi ölçü birimini kullandıklarını ve bunun bloktaki parametreyle eşleşip eşleşmediğini sorun.
|
| Bir öğrenci [Spin for] bloğunun parametresine “2 ¼ tur” girmek için ‘21/4’ girmeye çalışır. |
Kesirler ve ondalıklar aynı şekilde yazılır. Öğrenci kesri ondalık sayıya dönüştürmüyor. |
Öğrencilere, tanınabilir parametreler olmaları için kesirleri ondalık sayılara dönüştürmeleri gerektiğini hatırlatın. Bunu yapmak için payı paydaya bölün. 2 ¼=94 =2,25 Öğrencilerden sık kullanılan kesirli değerleri ve bunların ondalık eşdeğerlerini grafiksel olarak göstermelerini ve kendi kaynaklarını oluşturmalarını isteyebilirsiniz. |
|
Öğretmen öğrencilerden tekerlek çevresi hesaplamalarını paylaşmalarını ister. Öğrenci cevapları |
Çevre yarıçapı -πxyarıçapı kullanılarak hesaplanır. Öğrenci hesaplamada yanlış ölçüm kullanıyor. |
Öğrencilere çevreninπ x çapolduğunu ve çapın tekerleğin merkezinden geçen düz bir çizgi (veya yarıçapın iki katı) olduğunu hatırlatın.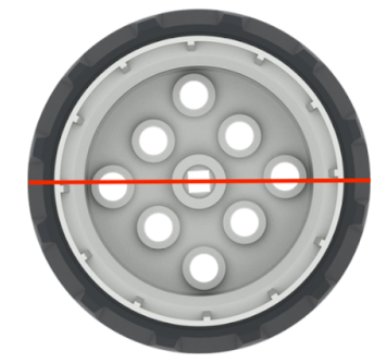 Eğer birçok öğrenci formülleri kullanmada zorluk çekiyorsa, tüm sınıf etkinliği olarak değeri ölçmek ve hesaplamak isteyebilirsiniz. |
Öğrencilere, hesaplamalarının yalnızca parametre doğru birime ayarlanırsa amaçlandığı gibi çalışacağını hatırlatın. Dönüşler ve dereceler aynı değer değildir.
Örnek Çözümler
Lab 4 Örnek Çözümü
*Not: Örnek projede ilk blokta 've bekleme' ifadesi kullanılmıştır, böylece her iki blok da aynı anda yürütülecektir. ‘Ve beklemeyin’ olmadan, ilk motor, sonra ikincisi döner ve Kod Tabanı amaçlandığı gibi sürmez. Öğrencilerin projeyi 'çökertmediğinden' ve beklemediğinden 'emin olun, aksi takdirde projeleri amaçlandığı gibi çalışmayacaktır.
Geçit töreni rotasının 48 inç (~122 cm) uzunluğunu sürmek için, Kod Tabanının ~7.68 tur gitmesi gerekecektir. Hesaplama solda, örnek VEXcode GO çözümü ise sağda gösterilmektedir.
Lab 5 Örnek Çözümü
Geçit töreni rotasının 48 inç (~122 cm) uzunluğunu sürmek ve 180 derece dönmek için, Kod Tabanının ~7,68 tur ileri gitmesi, ardından bir motoru ileri ve diğerini ~ 1,47 tur geri döndürmesi gerekecektir. Hesaplama sağda örnek VEXcode GO çözümü ile birlikte gösterilmiştir.
Not: Dönüş yerine derece kullanmak için dönüş hesaplamalarını 360 ile çarpın.
Uzatma Geçit Töreni Rotası
Öğrencilerin ekstra bir zorluğa ihtiyacı varsa, geçit töreni rotasını birçok farklı şekilde genişletebilirsiniz. Bu, olası bir çözümü olan bir örnektir.
Olası bir geçit töreni rotası uzantısı Bu örnek rotada, sürüş mesafeleri ve dönüşler Laboratuvarlardan yarıya indirilir. Ancak bu rotada, dönüşlerin yönü önemlidir. Öğrencilerin yeniden hesaplamanın yanı sıra, tekerleklerin istenilen yöne dönmesi için hangi yönlerin kullanılacağını da bulmaları gerekecektir.
Önceki Lab'lardan yarıya indirilmiş hesaplamalar şu şekildedir:
Sürüş mesafesi = ~ 3,84 dönüş
Dönüş mesafesi = ~ 0,73 dönüş
Bu değerler aşağıdaki VEXcode GO çözümü örneğinde kullanılmaktadır:
