Achtergrond
Hulpmiddelen worden elke dag door mensen gebruikt om hen te helpen taken uit te voeren en problemen op te lossen. Deze getallenlijn: optel-eenheid zal u en uw studenten vertrouwd maken met specifieke tools die helpen bij het oplossen van optelvergelijkingen. De tools die je studenten zullen gebruiken, zijn onder meer een 123 Robot, een getallenlijn en manipulatieven. Studenten zullen ook leren hoe ze hun 123 Robot op een getallenlijn effectief kunnen verplaatsen om vergelijkingen op te lossen.
Nummerregel
Een getallenlijn is een getallenlijn die met bepaalde tussenpozen of gelijke spaties is gemarkeerd met getallen die in een bepaalde volgorde zijn geplaatst. De getallen stijgen positief vanaf nul en dalen negatief vanaf nul. Het is een handig hulpmiddel voor het optellen en aftrekken van getallen. Bovendien helpt de getallenlijn studenten om getallen te visualiseren terwijl ze problemen oplossen. De getallenlijn helpt ook om een één-op-één correspondentie weer te geven. Eén-op-één correspondentie is de mogelijkheid om één object te koppelen aan één (corresponderend) nummer of object. Studenten zullen weten dat één beweging van de 123 Robot op de getallenlijn gelijk is aan het getal één dat in een vergelijking wordt toegevoegd.
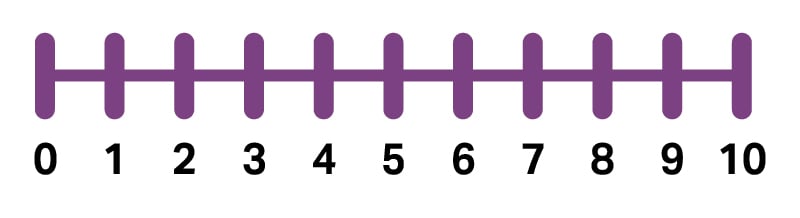
Telstrategieën
Studenten gebruiken verschillende telstrategieën wanneer ze beginnen met het leren van optellen en aftrekken. Dit feit is vastgelegd in de volgende Common Core Math Standard voor het eerste leerjaar: relateer tellen aan optellen en aftrekken (bijv. door op 2 te tellen om 2 toe te voegen). Deze standaard staat centraal in dit STEM-lab. Er zijn verschillende telstrategieën voor zowel optellen als aftrekken, waaronder alles tellen, rekenen en terugtellen.
Wanneer studenten de telstrategie gebruiken (voor optellen en aftrekken), beginnen ze met 1 en tellen ze om het totale aantal objecten te vinden. Bijvoorbeeld, 7 + 2, de student zou beginnen te tellen van 1, tot 7 tellen en nog 2 tellen: 1, 2, 3, 4, 5, 6, 7...8, 9.
Een andere strategie die studenten kunnen gebruiken is het rekenen op strategie (voor optellen), studenten tellen vanaf het startnummer in plaats van vanaf 1. Bijvoorbeeld, 7 + 2, de studenten zouden beginnen bij 7...8, 9. Met behulp van het tellen op strategie (voor aftrekken) beginnen studenten echter met het subtrahendgetal en rekenen ze erop om het totaal te bereiken. Bijvoorbeeld, 12-5, de student zou beginnen met 5 en tellen tot 12 door enen: 5...6, 7, 8, 9, 10, 11, 12.
De laatste strategie die hierboven is genoemd, terugtellen, gebeurt wanneer studenten aftrekproblemen oplossen. Studenten die de telstrategie gebruiken, beginnen met het totaal en tellen vervolgens het getal terug dat wordt afgetrokken. Bijvoorbeeld, 12-5, studenten beginnen met 5 en tellen tot 12 door enen, 5...6, 7, 8, 9, 10, 11, 12.
Terwijl je oefent met het oplossen van problemen met je studenten, moet je je bewust zijn van een veelvoorkomende misvatting bij studenten over dubbeltellen. Als een student bijvoorbeeld 3 + 5 optelt, kan hij beginnen bij 3 en eindigen met een antwoord van 7 in plaats van te rekenen op 3 en te eindigen met het juiste antwoord van 8.
Het komt veel voor dat studenten hun vingers gebruiken om te tellen of te helpen bij het oplossen van optel- en aftrekvergelijkingen. Omdat studenten andere telstrategieën begrijpen en gebruiken, moeten studenten licht worden ontmoedigd om hun vingers te gebruiken bij het oplossen van optel- en aftrekvergelijkingen. Ondersteunen en oefenen terwijl studenten een goed begrip van de telstrategieën ontwikkelen, wordt aangemoedigd om verbindingen te leggen met meer geavanceerde strategieën in hun toekomstige leerproces.
Manipulatieven
Manipulatieven zijn fysieke objecten die in praktische leerervaringen worden gebruikt om een concept weer te geven. In dit apparaat zijn kleurpotloden de voorgestelde manipulatieven. Manipulatieven zijn nuttig voor studenten bij het oplossen van wiskundige vergelijkingen, omdat de studenten de getallen die ze bij elkaar optellen kunnen visualiseren. De manipulatieven ondersteunen studenten ook bij het relateren van tellen aan optellen en aftrekken. Studenten wordt gevraagd om de manipulatieven te tellen om tijdens de activiteiten hetzelfde aantal te hebben als de som van het optelprobleem. Dit is een geweldige manier voor studenten om hun werk te controleren om ervoor te zorgen dat de manipulatieven overeenkomen met het antwoord op de vergelijking die studenten mogen doen in Lab 2 Play Part 1 en Play Part 2.
Eén-op-één correspondentie
Het wordt meestal uitgelegd als de mogelijkheid om één object te koppelen aan één (corresponderend) nummer of object.
-
Voorbeeld: 1 druk op de knop op de 123 Robot = 1 beweging

1 druk op de knop 
1 robotbeweging
Algoritme
Algoritmen zijn een lijst met goed gedefinieerde instructies om een specifiek probleem op te lossen of een taak uit te voeren. Algoritmen verwijzen meestal naar computerimplementeerbare instructies, maar kunnen ook andere instructies bevatten over hoe je je tanden moet poetsen of complexere taken zoals het bedienen van een jetski.
Tijdens deze unit volgen studenten een reeks instructies in een specifieke volgorde om de 123 Robot te bedienen. Zie het artikel De VEX 123 Robot Vex-bibliotheek gebruiken voor meer informatie over het gebruik van de 123 Robot. Voor informatie over het coderen van de 123 Robot met behulp van Touch-knoppen, zie het artikel Codering met de Touch-knoppen op de 123 Robot VEX Library.
Het algoritme om de 123 Robot te verplaatsen is:
- Push to Wake
- Raak aan om te coderen
- Schudden om te wissen
