Evaluate and Explain
Reading Code Sequences to Choose a Preferred Solution
As your class worked on the Play section, you probably noticed that there were many different solutions to the same problem that was presented. That is something that happens often in the world of programming. While there can be different ways to do something, everyone will have a preferred method or solution, and that could be based on a number of factors. In this activity, your group will look at 3 possible code block solutions to a problem, figure out if they work in the intended fashion, then choose a preferred solution from the group and explain why you chose it.
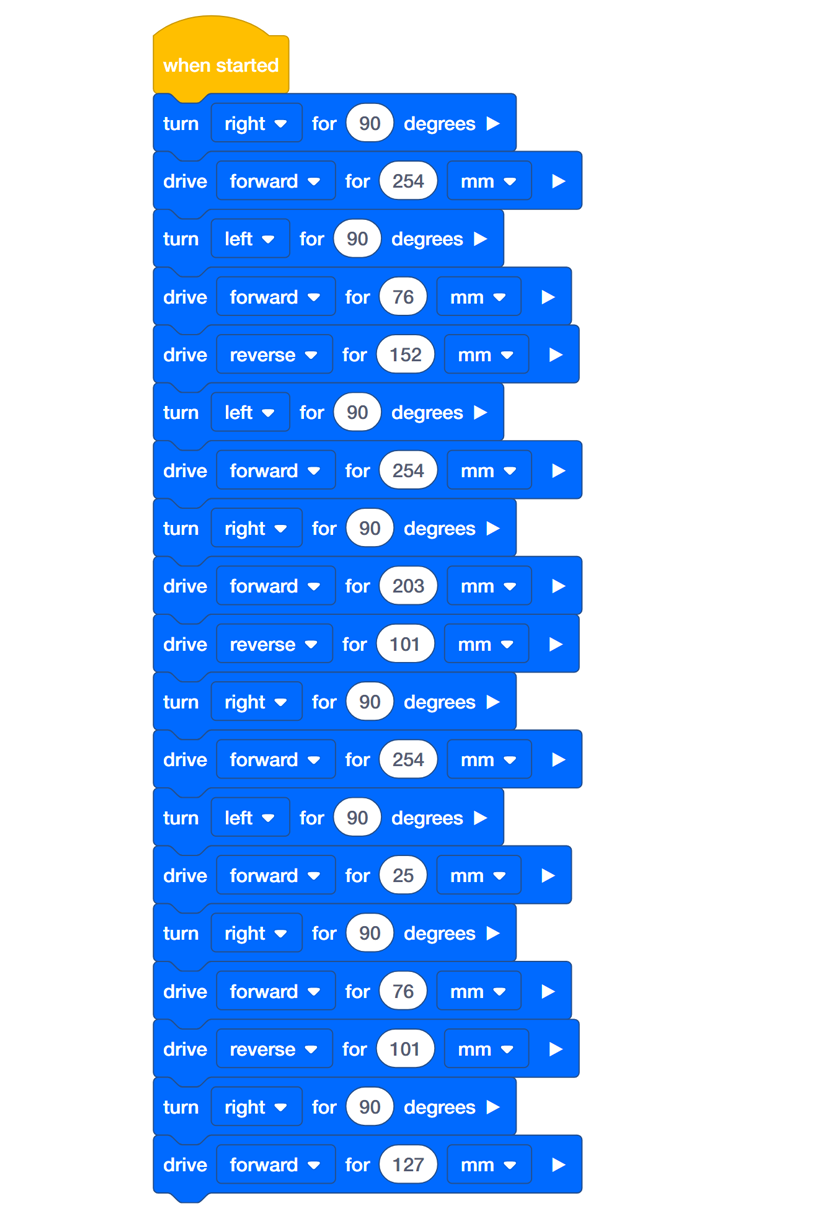
The problem: Create a sequence that, when the robot begins at the Start, will travel into and out of all 3 classrooms (in any order) and return to the End point. The robot must navigate around the stairs, and can go through the doorways marked by the small rectangles on the map image.

- For each solution below, answer these 3 questions in your engineering notebook:
- Does this code accomplish the task? Why or why not?
- If it does work, what are the advantages of this code over the others?
- What are the disadvantages of this code over the others?
- Most of the time, programming is evaluated on its efficiency, and the preferred solution is one that accomplishes the goal in the most efficient way possible.
Click on the solutions below to see a larger image.





What is Code Efficiency?
If you needed to get 3 things from your kitchen, you would probably go get all 3 things in one trip, instead of making 3 separate trips. Why? Because it would be more efficient. Efficient means “achieving maximum productivity with minimum wasted effort or expense.” So how does that connect to programming?
Code efficiency means that a program is written to work well and quickly, using the least amount of work, or steps, properly, while still doing its job. It is important because it reduces the risk of a program not functioning well, and in turn, causing problems for other parts of a program that are running around it. The efficiency of a code can be a measure of quality, and when we write projects in VEXcode IQ block, we are often looking for the most “efficient” project as the preferred solution.
Basically, code efficiency is a principle that means you want to write a code that accomplishes your goal using the fewest commands, or blocks, possible.
In your Engineering Notebook, answer the following questions:
- With code efficiency in mind, which is your preferred solution and why?
- Do you think that is the best solution, why or why not?