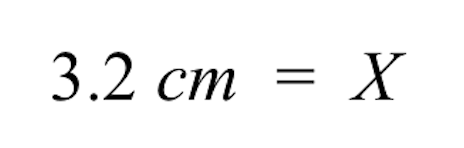Skip to main content
Teacher Portal

Understanding Scale

Teacher Toolbox icon Teacher Toolbox - The Purpose of This Page

The purpose of this page is to provide practice and context for the scaling that the students will need to complete in Designing and Scaling a Race Course and later in the Robo Rally Challenge.

Engage the students in a whole class discussion to review the Motivate Discussion questions. Ask the students to write their work and thoughts in their engineering notebook.

Cartoon map of the world with a scale grid overlay and a ruler to symbolize the concept of scale.
Using scale is an important skill to learn.

What is "Scale"?

Scale is the relationship or ratio between a set distance on a map or drawing and its corresponding distances in real life. Materials that use scale, such as blueprints, are often considered more valuable because they allow the user to perceive distance visually, therefore making them more effective models. Being able to convert measurements when working with scale is important for careers that incorporate maps, blueprints, and architectural models. Professionals such as architects, engineers, military soldiers, and set designers all use scale in some fashion in their industry.

Developing a detailed sketch as a plan is an important step in the engineering design process. When we make a scaled copy of an object, the original and the copy must have the same proportions. To present how much an object has actually been scaled down (or up), we often use ratios. These ratios are displayed on the scaled copy so that the real-life object can be represented correctly. For example, a scale on a drawing may be represented as 1 cm = 20 m. This lets a team know that for every 1 cm on the sketch, the real-life measurement is 20 m. So, if a wall is represented on the sketch as 4 cm, the real-life wall needs to be 80 m. When engineers construct things like highways or buildings, the scaled plans are checked continuously to make sure the proportions are always correct. Breaking the real-life model down into sections and checking that the proportions are correct while completing each section is one way teams work to make sure that they are keeping to scale. Mistakes can cause a loss of substantial time, money and materials, so keeping with the accuracy of the scale is essential.

Motivate Discussion icon Motivate Discussion

Scaling can be a difficult concept for some students to apply. Instead of having students drill and practice the mathematics involved, have a discussion so that students can explain to classmates how they reason about scaling.
Q: A red building in a drawing of the city is 2 centimeters tall but it is really 50 meters tall. The gray building next to it in the drawing is only 1 centimeter tall. How tall is that next building really?
A: It is really 25 meters tall. See the explanation below:

Proportions show that two ratios are equal.

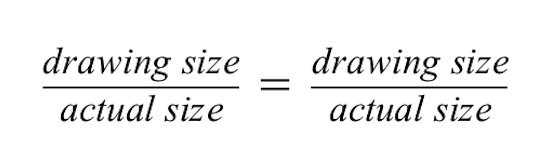
Two ratio examples are equal. Each side is identical. The first ratio reads 'drawing size over actual size' and the second ratio reads 'drawing size over actual size'.

For the ratio on the left, we know that the drawing of the red building is 2 cm tall but the actual size of the red building is 50 meters.

  • Notice the drawing size is in the numerator and the actual size is in the denominator. It is important to keep these the same for both ratios so that they remain equal.
  • Since we know that the drawing size of the gray building is 1 cm, we will put this in the numerator in the second ratio.
  • The actual size of the gray building will go in the denominator, but we do not know this size yet, we need to calculate. So, for now we will put the variable X there.

Two ratios are equal. The first ratio reads 'two centimeters over fifty meters' and the second ratio reads 'one centimeter over the variable X'.

To solve for the variable X, the unknown actual size of the gray building, we can use the method of cross multiplication.

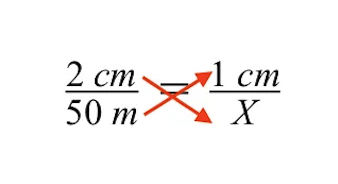
The two ratios are shown the same as before, but now there are arrows indicating cross multiplication. Again, the first ratio reads 'two centimeters over fifty meters' and the second ratio reads 'one centimeter over the variable X'.

Using cross multiplication gives us the following. The next step is to solve for the unknown size of the gray building designated by the variable X.

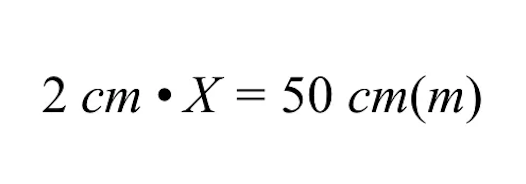
The result of the cross multiplication is an equation of 'two centimeters multiplied by the variable X is equal to fifty centimeters multiplied by one meter'.

To solve for X, we must undo the multiplication of 2 cm times the variable X by dividing both sides of the equation by 2 cm.

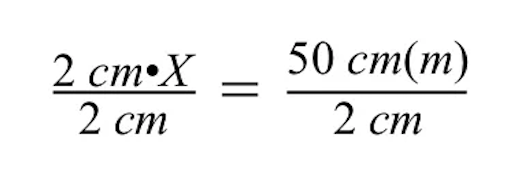
This equation is similar to the one we had in the last step, but now both sides are divided by two centimeters. It now reads 'two centimeters multiplied by the variable X divided by two centimeters is equal to fifty centimeters multiplied by one meter divided by two centimeters'.

Notice when dividing both sides by 2 cm, the units of cm cancel on the left and right sides of the equal sign, leaving just meters (m) on the right side.

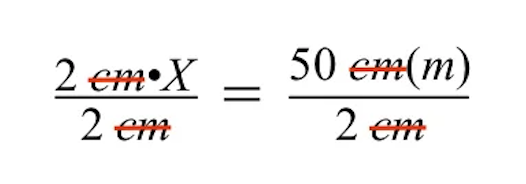
The equation is the same as the last step, but all of the 'centimeter' terms are crossed out. It now reads 'two multiplied by the variable X divided by two is equal to fifty meters divided by two'.

Simplifying further, we see the left side reduces to just our unknown actual size of the gray building, represented by the variable X.

  • On the right side, we are left with 25 m. Thus, the unknown actual size of the gray building is 25 m.
  • This is reasonable, because if 2 cm for the drawing size is proportional to 50 meters for the actual size, then cutting that in half for 1 cm should equate to 25 meters.

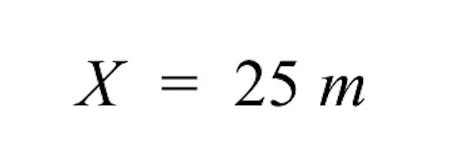
The final result is an equation defining the variable X. It reads 'the variable X is equal to twenty five meters'.

Q: What if we wanted to add a brick building that is really 80 meters tall to the drawing? How many centimeters should it be?
A: 3.2 centimeters. See the explanation below:

Proportions show that the two ratios are equal.

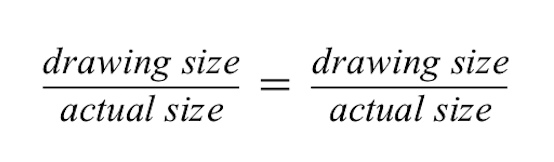
Two ratio examples are equal. Each side is identical. The first ratio reads 'drawing size over actual size' and the second ratio reads 'drawing size over actual size'.

For the ratio on the left, we know that the drawing of the red building is 2 cm tall but the actual size of the red building is 50 meters.

  • Notice the drawing size is in the numerator and the actual size is in the denominator. It is important to keep these the same for both ratios so that they remain equal.
  • Since we know that the drawing size of the gray building is 1 cm, we will put this in the numerator in the second ratio.
  • The actual size of the gray building will go in the denominator, but we do not know this size yet, we need to calculate. So, for now we will put the variable X there.

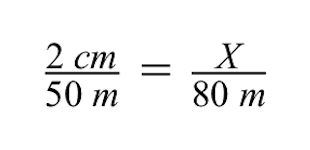
Two ratios are equal. The first ratio reads 'two centimeters over fifty meters' and the second ratio reads 'the variable X over eighty meters'.

To solve for the variable X, the unknown drawing size of the brick building, we can use the method of cross multiplication.

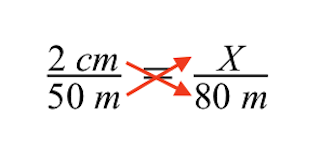
The two ratios are shown the same as before, but now there are arrows indicating cross multiplication. Again, the first ratio reads 'two centimeters over fifty meters' and the second ratio reads 'the variable X over eighty meters'.

Using cross multiplication gives us the following. The next step is to solve for the unknown size of the gray building designated by the variable X.

The result of the cross multiplication is an equation of 'one hundred and sixty centimeters multiplied by one meter is equal to fifty meters multiplied by the variable X'.

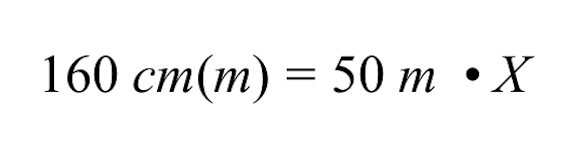
To solve for the variable X, we must undo the multiplication of 50 m times X by dividing both sides by 50 m.

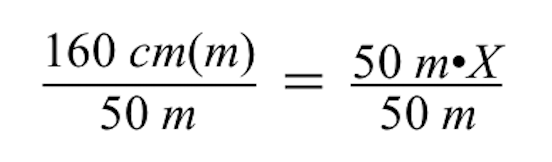
This equation is similar to the one we had in the last step, but now both sides are divided by fifty meters. It now reads 'one hundred and sixty centimeters multiplied by one meter divided by fifty meters is equal to fifty meters multiplied by the variable X divided by fifty meters'.

Notice when dividing both sides by 50 m, the units of m (meters) cancel on the left and right sides of the equal sign, leaving just centimeters (cm) on the left side.

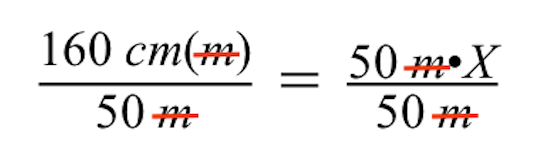
The equation is the same as the last step, but all of the 'meter' terms are crossed out. It now reads 'one hundred and sixty centimeters divided by fifty is equal to fifty multiplied by the variable X divided by fifty'.

Simplifying further, we see the right side reduces to just our unknown drawing size of the brick building, represented by the variable X.

  • On the left side, we are left with 3.2 cm. Thus, the unknown drawing size of the brick building is 3.2 cm.

The final result is an equation defining the variable X. It reads 'the variable X is equal to three point two centimeters'.

<  Back Return to Labs Next  >