Scaling in Architecture
![]() Teacher Toolbox
-
The Purpose of this Section
Teacher Toolbox
-
The Purpose of this Section
This Apply section will help students understand how robots are used in the real world. Begin the section by asking students to identify some of the largest buildings in the world. List the students’ answers in the classroom so they can be referenced after the reading. The Apply section also discusses how using conversion factors and scaling can be used in a VEX competition setting.
These Apply pages can be worked through as a class.
-
Together, read the Apply page “Scaling in Architecture.”
-
Facilitate a class discussion on the topic using the Motivate Discussion questions. Encourage students to document their work and thoughts in their engineering notebooks.
-
Together, read the page “The Advantage of Robot Math.”
-
Facilitate a class discussion on the topic using the Motivate Discussion questions. Encourage students to document their work and thoughts in their engineering notebooks.
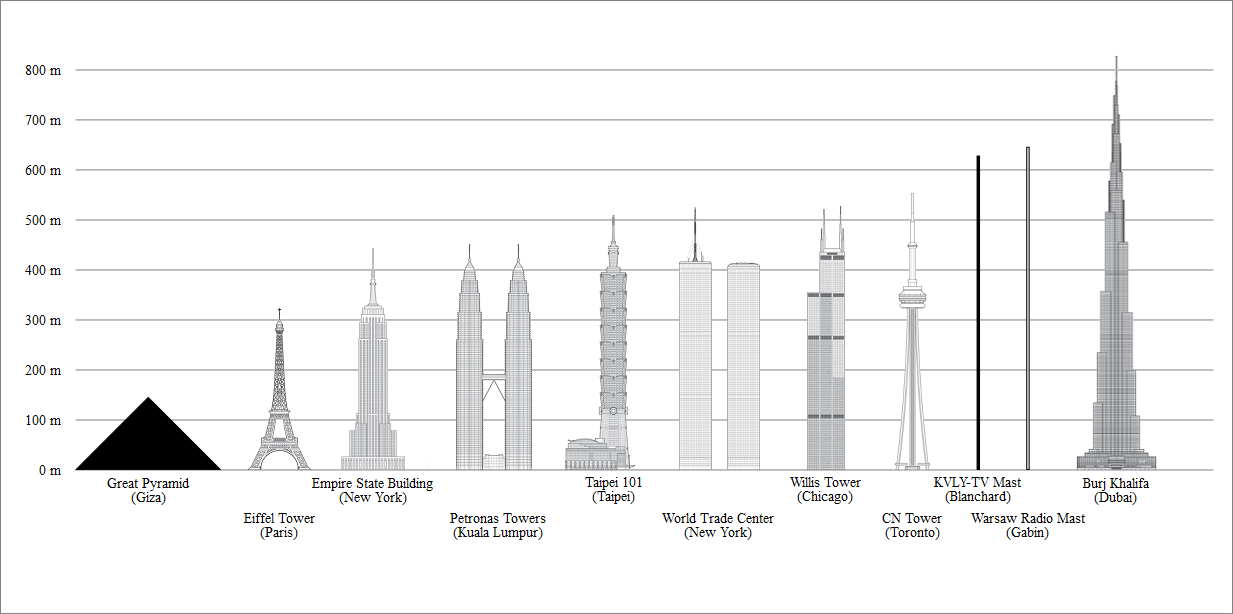
An architect is a person who designs buildings or other structures. Architects need to draw scaled-down blueprints or images in order to design structures that are appropriate in size, height, etc. Could you imagine only having a small piece of land to build a building on, and it did not fit? Especially in areas that are limited on the amount of space they can use such as clustered cities. Architects scale their blueprints to size so that they fully understand how much material they need as well as make sure everything will fit properly.
There have been many famous architects throughout history. Some well-known structures include the Parthenon in Athens, Greece, and the Burj Khalifa in Dubai, which has been the tallest building in the world since 2009 at a total height of 829.8 m. However, the Jeddah Tower in Saudi Arabia scheduled to open in 2020 will become the world's tallest skyscraper. Intricate planning and calculations were required for such vast and complex structures to be built properly.
Scaling structures in the form of blueprints and sketches not only allows the designer to plan accordingly. Scaling also allows structures and buildings to be compared to each other. The image above required scaling in order to compare the relative sizes of the structures next to each other. Each actual size of 100 m is represented by approximately 10 mm on the drawing. You can view the ratio of drawing size/actual size as 10 mm/ 100 m.
![]() Motivate Discussion
Motivate Discussion
Q: In what other scenarios other than architecture would scaling be beneficial?
A: Answers may vary, but some examples could include showing objects such as model cars or the planets in the solar system. Both are extremely large in daily life, but can be scaled down to observe and even touch.
Q: The Empire State Building stands a total of 443.2 m tall. Using the ratio of 10 mm/ 100 m, how many mm tall is it if you were to draw it?
A: The drawing size of the Empire State Building is 44.32 mm. Actually measure the drawing using meter stick or ruler - how close is the scale?
Math explanation:
Proportions show that two ratios are equal.

For the ratio on the left, we are using the ratio that the drawing is is 10 mm tall but the actual size is 100 meters.
- Notice the drawing size is in the numerator and the actual size is in the denominator. It is important to keep these the same for both ratios so that they remain equal.
- Since we know that the actual size of the Empire State Building is 443.2 m, we will put this in the denominator in the second ratio.
- The drawing size of the Empire State Building will go in the numerator, but we do not know this size yet, we need to calculate. So, for now we will put the variable X there.

To solve for X, the unknown drawing size of the brick building, we can use the method of cross multiplication.

Using cross multiplication gives us the following. The next step is to solve for the unknown drawing size of the Empire State Building designated by X.

To solve for X, we must undo the multiplication of 100 m times X by dividing both sides by 100 m.

Notice when dividing both sides by 100 m, the units of m cancel on the left and right sides of the equal sign, leaving just millimeters (mm) on the left side.

Simplifying further, we see the right side reduces to just our unknown drawing size of the Empire State Building, represented by the variable X.
- On the left side, we are left with 44.32 mm. Thus, the unknown drawing size of the Empire State Building is 44.32 mm.
