Skip to main content

Calculating Two Gear Ratios

Now that you have explored what gears are and how they can be used to create a mechanical advantage, you will now calculate different gear ratios and combine them to obtain a compound gear ratio.

You will work in groups of four to calculate gear ratios and determine the resulting mechanical advantage.

View an example

Begin by viewing the following example:

A table shows Gear Ratio number in the first column, calculations in the center column, and ratio in the third column. The first row reads Gear ratio 1 with the calculations for a 12T Driven gear over a 36T Driving gear, and the ratio of 1:3. The second row reads Gear Ratio 2, with the calculations for a 12T Driven gear over a 60T driving gear, and a ratio of 1:5. The third row reads Resulting Ratio, with calculations to multiple 1 over 3 by 1 over 5 for a ratio of 1 to 15. The final row reads Advantage and the Calculations read Increased speed: The 36T driving input gear will turn once for the 12 T driven output gear to turn 15 times.

In the example above, the Resulting Ratio row refers to calculating the Compound Gear Ratio by multiplying all of the individual gear ratios together.

Gear Ratio 1 has a 36 tooth-gear (36T gear) driving a 12 tooth-gear (12T gear). Viewing the relationship is Driven over Driving results in 12 over 36, which reduces down to one third. Thus, the ratio is 1:3.

Row one of the previous table shows Gear Ratio 1 with the calculations resulting in a ratio of 1 to 3.

Similarly for Gear Ratio 2, a 60T gear is driving a 12T gear. Viewing the relationship as Driven over Driving results in 12 over 60, which reduces to one fifth. Thus, the ratio is 1:5.

The second row from the table above, reading Gear ratio 2 with the calculations for a ratio of 1 to 5.

To combine these two ratios, fraction multiplication is introduced. One third times one fifth is one fifteenth. Keep in mind, when multiplying fractions, you multiply straight across in the numerator and denominator. Thus, the compound gear ratio is 1:15.

The third row of the above table reading Resulting ratio, with the calculations resulting in a 1 to 15 ratio.

Once the compounded gear ratio is calculated, it can now be determined what the mechanical advantage is. The resulting advantage is Increased Speed: The 36T driving (input) gear will turn once for the 12T driven (output) gear to turn 15 times.

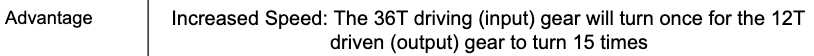
The fourth row of the above table stating the Advantage being increased speed.

Calculation 1

Fill in the missing calculations from the Gear Ratio table. Keep in mind, each person should be calculating according to their role.

Table for calculating gear ratios with missing values. Gear ratio 1 shows 36T on the Driven gear and 12T on the Driving gear with other values blank. Gear ratio 2 shows 60T driven gear and a 12T driving gear with other values blank. Resulting ratio and the type of advantage values are blank as well.

  • Role 1: Calculate the Gear Ratio 1 row of the above table. Show all work in your engineering notebook.
  • Role 2: Calculate the Gear Ratio 2 row of the above table. Show all work in your engineering notebook.
  • Role 3: Calculate the Resulting Ratio row of the above table. Check the calculations from Gear Ratio 1 and 2 before calculating the final compound gear ratio. Show all work in your engineering notebook.
  • Role 4: Calculate the Advantage row of the above table. Show all work in your engineering notebook.
  • All Roles: Once the table is completed, verify with all group members that the calculations are correct.
<  Back Return to Labs Next  >