Škálování v architektuře
![]() Sada nástrojů
této části
Sada nástrojů
této části
Tato aplikační část pomůže studentům pochopit, jak se roboti používají v reálném světě. Začněte tuto část tím, že požádáte studenty, aby určili některé z největších budov na světě. Odpovědi studentů si ve třídě vyznačte, aby se na ně po přečtení mohli odvolávat. Sekce Aplikace také popisuje, jak lze použití konverzních faktorů a škálování využít v prostředí soutěže VEX.
Tyto stránky Apply lze zpracovat jako třídu.
-
Společně si přečtěte stránku s názvem „Škálování v architektuře“ v části „Použít“.
-
Veďte třídní diskusi na dané téma pomocí otázek Motivate Discussion. Povzbuďte studenty, aby si svou práci a myšlenky zapisovali do svých technických sešitů.
-
Společně si přečtěte stránku „Výhoda robotické matematiky“.
-
Veďte třídní diskusi na dané téma pomocí otázek Motivate Discussion. Povzbuďte studenty, aby si svou práci a myšlenky zapisovali do svých technických sešitů.
 Zdroj
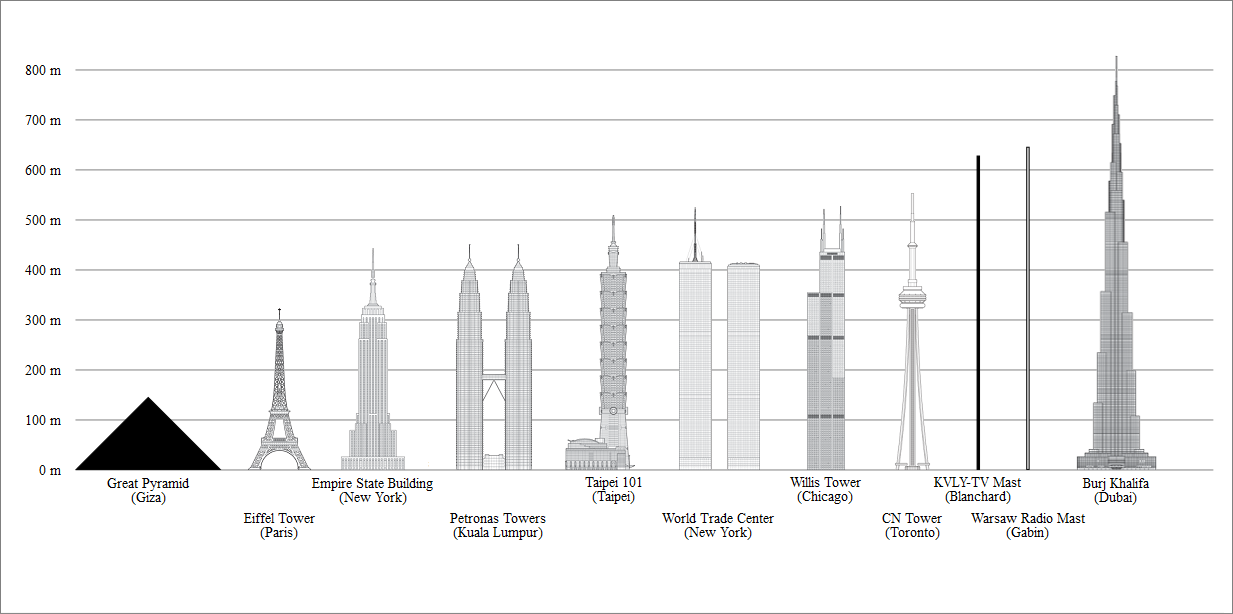
Zdroj Architekt je osoba, která navrhuje budovy nebo jiné stavby. Architekti musí nakreslit zmenšené plány nebo obrázky, aby navrhli struktury, které jsou vhodné co do velikosti, výšky atd. Dokážete si představit, že byste měli jen malý pozemek, na kterém byste postavili budovu, a ten se vám nevešel? Zejména v oblastech, které jsou omezeny množstvím prostoru, který mohou využít, jako jsou například seskupená města. Architekti upravují své plány na míru, aby plně pochopili, kolik materiálu potřebují, a také aby se ujistili, že vše správně sedí.
V průběhu historie existovalo mnoho slavných architektů. Některé známé stavby zahrnují Parthenon v Aténách v Řecku a Burj Khalifa v Dubaji, která je od roku 2009 nejvyšší budovou na světě s celkovou výškou 829,8 m. Jeddah Tower v Saúdské Arábii, která má být otevřena v roce 2020, se však stane nejvyšším mrakodrapem na světě. Pro správnou výstavbu takových rozsáhlých a složitých staveb bylo nutné složité plánování a výpočty.
Změna měřítka struktur ve formě plánů a skic nejen umožňuje projektantovi plánovat podle toho. Škálování také umožňuje vzájemné porovnání konstrukcí a budov. Výše uvedený obrázek vyžadoval změnu měřítka, aby bylo možné porovnat relativní velikosti struktur vedle sebe. Každá skutečná velikost 100 m je na výkresu reprezentována přibližně 10 mm. Poměr velikosti výkresu/skutečné velikosti můžete zobrazit jako 10 mm/ 100 m.
![]() Motivovat diskusi
Motivovat diskusi
Otázka:V jakých dalších scénářích kromě architektury by bylo škálování prospěšné?
Odpověď:Odpovědi se mohou lišit, ale některé příklady by mohly zahrnovat zobrazení objektů, jako jsou modely aut nebo planety ve sluneční soustavě. Oba jsou v každodenním životě extrémně velké, ale lze je zmenšit, abyste je mohli pozorovat a dokonce se jich i dotknout.
Q:Empire State Building měří celkem 443,2 m. Kolik mm je výška budovy, pokud ji nakreslíte, s využitím poměru 10 mm/100 m?
A:Velikost výkresu Empire State Building je 44,32 mm. Změřte si výkres pomocí metrové tyče nebo pravítka - jak přesné je měřítko?
Matematické vysvětlení:
Poměry ukazují, že dva poměry jsou si rovny.

Pro poměr vlevo používáme poměr, který ukazuje výkres s výškou 10 mm, ale skutečná velikost je 100 metrů.
- Všimněte si, že velikost výkresu je v čitateli a skutečná velikost ve jmenovateli. Je důležité, aby tyto hodnoty byly pro oba poměry stejné, aby zůstaly stejné.
- Protože víme, že skutečná velikost Empire State Building je 443,2 m, dosadíme tuto hodnotu do jmenovatele ve druhém poměru.
- Velikost výkresu Empire State Building uvedeme v čitateli, ale tuto velikost zatím neznáme, musíme ji vypočítat. Takže prozatím tam umístíme proměnnou X.

Pro vyřešení X, neznámé výkresové velikosti cihlové budovy, můžeme použít metodu křížového násobení.

Použití křížového násobení nám dává následující. Dalším krokem je vyřešit neznámou velikost výkresu Empire State Building označenou X.

Abychom vyřešili X, musíme vzít zpět násobení 100 m krát X vydělením obou stran číslem 100 m.

Všimněte si, že při dělení obou stran číslem 100 m se jednotky m na levé a pravé straně znaménka rovnosti zruší, takže na levé straně zůstanou pouze milimetry (mm).

Zjednodušíme-li to dále, vidíme, že se pravá strana zmenšuje na naši neznámou velikost výkresu Empire State Building, reprezentovanou proměnnou X.
- Na levé straně nám zbývá 44,32 mm. Neznámá velikost kresby Empire State Building je tedy 44,32 mm.
