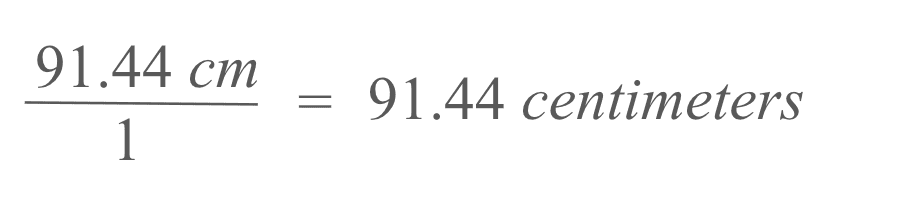Converting Units
Vocabulary
The following mathematical vocabulary will be used throughout this STEM Lab:
- Proportion: When two ratios are equal.
- Ratio: A mathematical comparison of two values.
- Unit Ratio: A ratio with a denominator of 1.
- Conversion Factor: An expression for the equal exchange between units.
- Unit Conversion: The process of converting a measurement in one set of units to the same measurement in another set of units.
- Scale: The relationship or ratio between a set distance on a map, model or drawing and the corresponding measurement on the actual object.
- Scale Drawing: The drawing of an object that is proportional.

Changing Units Without Changing Measurements
Sometimes, different designers may use different sets of units. For example, much of the world uses metric units like meters and centimeters, but a few places in the world uses imperial units like feet and inches. If we have different ways of measuring things, we could easily get the wrong measurements!
When converting between measurements, it is helpful to use conversion factors. Here are some examples:
- 1 meter = 100 centimeters = 1000 millimeters
- 1 inch = 2.54 centimeters = 25.4 millimeters = 0.0254 meters
- 1 yard = 3 feet = 36 inches = 914.4 millimeters
- 1 kilogram = 1000 grams
- 1 liter = .001 cubic meters
How many inches is 5 meters? Use the conversion factor 1 inch = 0.0254 meters.
How many centimeters is 36 inches? Use the conversion factor 1 in = 2.54 cm.
Rewrite 36 inches as 36/1 to make cancellation easier.
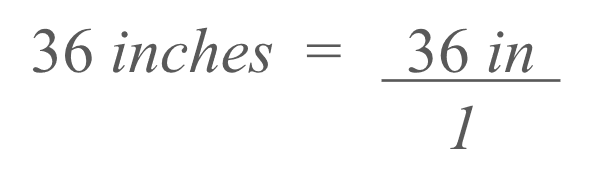
Multiply by the conversion factor of 2.54 centimeters = 1 inch.
It is important to understand that the conversion factor is equivalent to 1 and multiplying by it does not change any quantities.
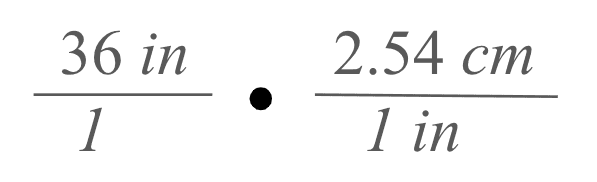
Notice here that the units of inches cancel since we have inches in the numerator and denominator. Thus, we are just left with the unit of centimeters. Fraction multiplication is carried out by multiplying straight across in the numerator and denominator.
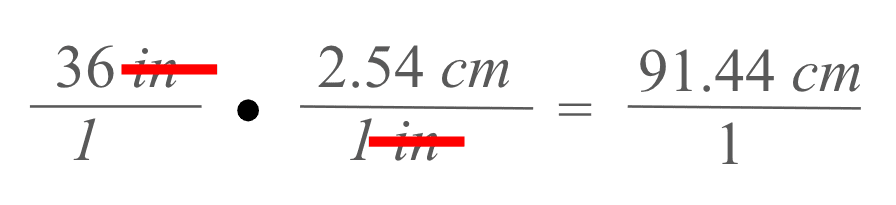
We see that 36 inches converts to 91.44 cm.