Schaalvergroting in architectuur
![]() Toolbox voor docenten
-
Het doel van deze sectie
Toolbox voor docenten
-
Het doel van deze sectie
In dit Toepassen-onderdeel krijgen leerlingen inzicht in hoe robots in de echte wereld worden gebruikt. Begin dit onderdeel door de leerlingen te vragen om enkele van de grootste gebouwen ter wereld te benoemen. Maak een lijst van de antwoorden van de leerlingen in de klas, zodat ze deze na het lezen kunnen raadplegen. In het gedeelte Toepassen wordt ook besproken hoe u conversiefactoren en schalen kunt gebruiken in een VEX-competitieomgeving.
Deze Toepassen-pagina's kunnen klassikaal worden doorgenomen.
-
Lees samen de pagina Toepassen ‘Schalen in architectuur’.
-
Leid een discussie in de klas over het onderwerp met behulp van de Motivate Discussion-vragen. Moedig leerlingen aan om hun werk en gedachten in hun technische notitieboekjes te documenteren.
-
Lees samen de pagina ‘Het voordeel van robotwiskunde’.
-
Leid een discussie in de klas over het onderwerp met behulp van de Motivate Discussion-vragen. Moedig leerlingen aan om hun werk en gedachten in hun technische notitieboekjes te documenteren.
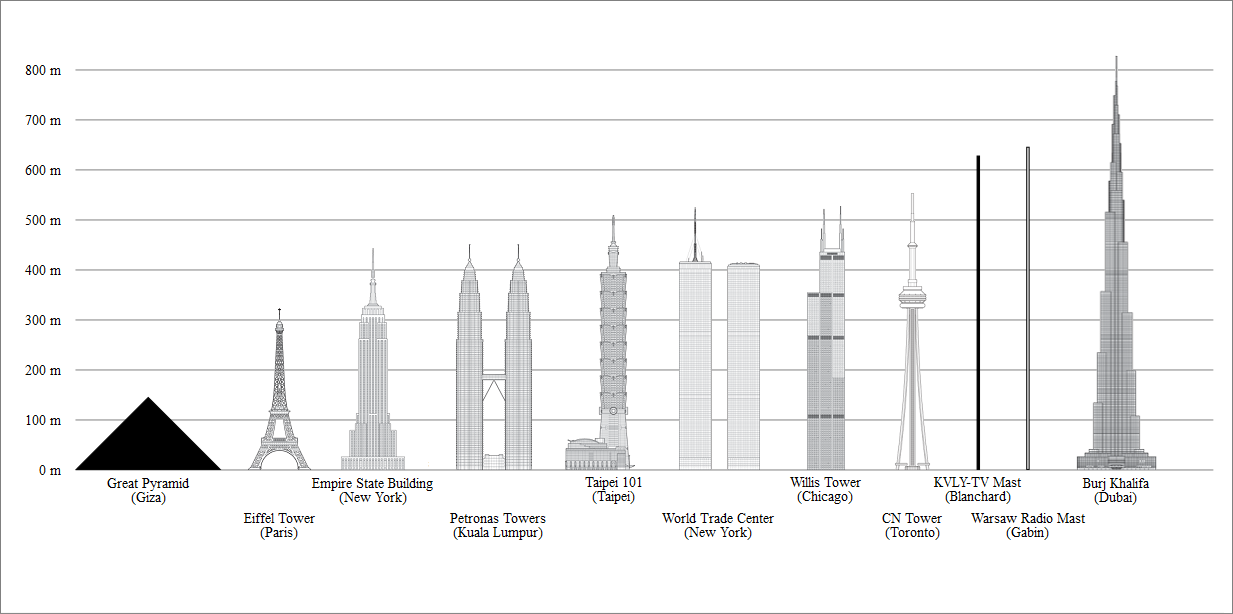
Een architect is een persoon die gebouwen of andere structuren ontwerpt. Architecten moeten verkleinde blauwdrukken of afbeeldingen tekenen om structuren te ontwerpen die geschikt zijn in grootte, hoogte, enz. Kun je je voorstellen dat je maar een klein stukje grond had om een gebouw op te bouwen en dat het niet paste? Vooral in gebieden die beperkt zijn in de hoeveelheid ruimte die ze kunnen gebruiken, zoals geclusterde steden. Architecten maken hun bouwtekeningen op maat, zodat ze precies weten hoeveel materiaal ze nodig hebben en zeker weten dat alles goed past.
Er zijn door de geschiedenis heen veel beroemde architecten geweest. Enkele bekende bouwwerken zijn het Parthenon in Athene, Griekenland, en de Burj Khalifa in Dubai, dat sinds 2009 met een totale hoogte van 829,8 m het hoogste gebouw ter wereld is. De Jeddah-toren in Saoedi-Arabië die in 2020 wordt geopend, wordt echter de hoogste wolkenkrabber ter wereld. Om zulke grote en complexe constructies op de juiste manier te kunnen bouwen, was een ingewikkelde planning en berekening nodig.
Door constructies in de vorm van blauwdrukken en schetsen op schaal te brengen, kan de ontwerper niet alleen zijn plannen hierop afstemmen. Door schaalvergroting kunnen ook structuren en gebouwen met elkaar worden vergeleken. De bovenstaande afbeelding vereiste schaalvergroting om de relatieve afmetingen van de structuren naast elkaar te vergelijken. Elke werkelijke afmeting van 100 m wordt op de tekening weergegeven door ongeveer 10 mm. U kunt de verhouding tekengrootte/werkelijke grootte bekijken als 10 mm/ 100 m.
![]() Motiveer discussie
Motiveer discussie
V:In welke andere scenario's dan architectuur zou opschalen nuttig zijn?
A:De antwoorden kunnen variëren, maar enkele voorbeelden zijn het tonen van objecten zoals modelauto's of de planeten in het zonnestelsel. Beide zijn in het dagelijks leven extreem groot, maar je kunt ze wel verkleinen om ze te bekijken en zelfs aan te raken.
Vraag:Het Empire State Building is in totaal 443,2 m hoog. Als je de verhouding 10 mm/100 m gebruikt, hoeveel mm is het gebouw dan hoog als je het zou tekenen?
A:De getekende afmeting van het Empire State Building is 44,32 mm. Meet de tekening op met een meetlat of liniaal: hoe nauwkeurig is de schaal?
Wiskundige uitleg:
Verhoudingen geven aan dat twee verhoudingen gelijk zijn.

Voor de verhouding links gebruiken we de verhouding dat de tekening 10 mm hoog is, maar de werkelijke grootte is 100 meter.
- Let op: de tekeninggrootte staat in de teller en de werkelijke grootte in de noemer. Het is belangrijk om deze waarden voor beide verhoudingen gelijk te houden, zodat ze gelijk blijven.
- Omdat we weten dat de werkelijke omvang van het Empire State Building 443,2 m is, zullen we dit in de noemer van de tweede verhouding invullen.
- De grootte van de tekening van het Empire State Building komt in de teller, maar deze maat weten we nog niet, die moeten we berekenen. Dus voor nu zullen we de variabele X daar plaatsen.

Om X, de onbekende tekeninggrootte van het bakstenen gebouw, op te lossen, kunnen we de methode van kruislingse vermenigvuldiging gebruiken.

Door kruislings vermenigvuldigen krijgen we het volgende: De volgende stap is het oplossen van de onbekende tekeninggrootte van het Empire State Building, aangegeven met X.

Om X te berekenen, moeten we de vermenigvuldiging van 100 m met X ongedaan maken door beide zijden te delen door 100 m.

Let op: wanneer u beide zijden deelt door 100 m, dan worden de eenheden van m aan de linker- en rechterkant van het gelijkteken opgeheven. Aan de linkerkant blijven alleen millimeters (mm) over.

Als we het nog verder vereenvoudigen, zien we dat de rechterkant wordt teruggebracht tot alleen de onbekende grootte van onze tekening van het Empire State Building, weergegeven door de variabele X.
- Aan de linkerkant houden we 44,32 mm over. De onbekende tekeninggrootte van het Empire State Building is dus 44,32 mm.
