Skip to main content

Výhoda „robotické matematiky“

Stránka sešitu týmového inženýrství zobrazuje vlevo náčrty cílů a destinací a vpravo popisy a výpočty. Každý diagram je podrobně popsán a vysvětluje účel výpočtu a jak to ovlivňuje další kroky.
Tým použije matematiku k naplánování trasy ve svém technickém sešitě.

Výhoda „robotické matematiky“

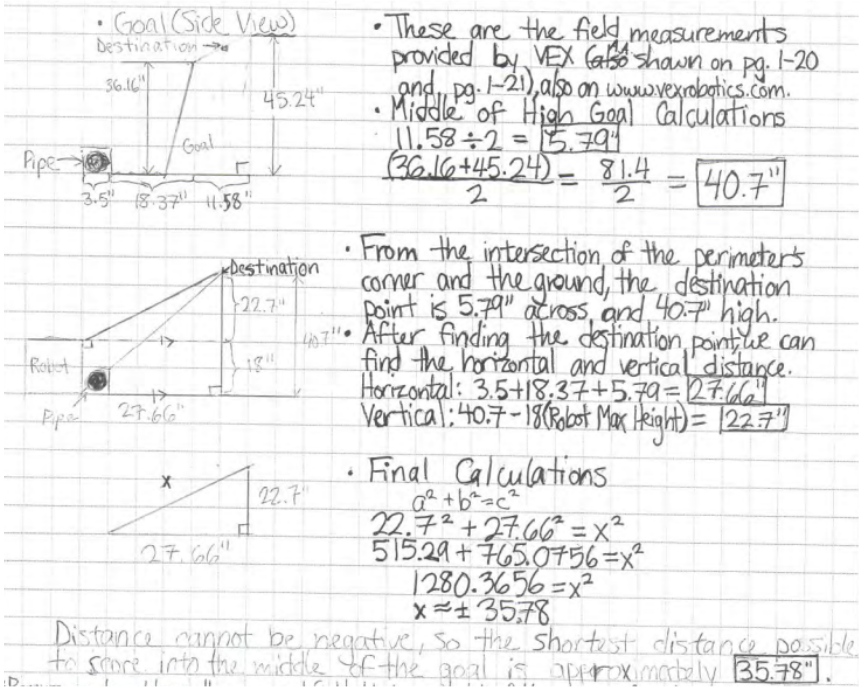
Robotické týmy, které efektivně využívají matematické koncepty, jako je proporcionální uvažování a měřítko, mají v soutěžích obvykle navrch. Když tyto týmy během soutěže vytvoří aliance s ostatními, mohou rychle provádět změny, jako je mapování nové trasy nebo určení správných hodnot rotace motorů pro své autonomní programy. Znalost matematických výpočtů, které se za změnami skrývá, může ušetřit drahocenný čas. Týmy pak tento čas využijí k provedení dalších fyzických nebo programových změn na svých robotech, které mohou zvýšit jejich šance na výhru. Používání „robotické matematiky“, jako je proporcionální uvažování a škálování, může rozhodně maximalizovat výkon týmu.

Na obrázku výše tým používá skutečná měření hřiště, která poskytl VEX, k výpočtu vzdáleností mezi různými místy na hřišti. Poté vypočítají nejkratší vzdálenost z konkrétního místa do plánovaného cíle. Toto jsou obzvláště důležité výpočty pro přesný pohyb robota během autonomního programu.

Ikona motivační diskuse Motivační diskuse - Aplikace matematiky v měřítku

Otázka:Proč byste místo hádání a ověřování používali „robotickou matematiku“?
Odpověď:Hádání a ověřování zabere příliš mnoho času. Navíc, pokud k určení, jak upravit robota nebo jeho program, použijete matematiku, můžete systematicky aplikovat změny na svá čísla/hodnoty namísto hádání a kontroly každé nové hodnoty.

Otázka:Kreslíte soutěžní pole VEX V5 na papír. Skutečné rozměry jsou necelých 12 x 12 stop, protože obvod vnitřního prostoru hřiště je 11,7 x 11,7 stop. Chcete to zmenšit tak, aby 1 stopa byla reprezentována 10 milimetry (mm). Poměr velikosti výkresu a skutečné velikosti je 10 mm / 1 stopa. Jaké jsou rozměry zmenšeného výkresu?
A:Rozměry v měřítku jsou 117 mm x 117 mm.

Matematické vysvětlení:

Poměry ukazují, že dva poměry jsou si rovny.

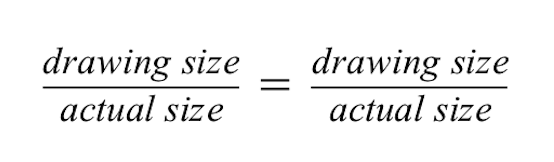
Dva příklady poměrů jsou si rovny. Každá strana je identická. První poměr zní „velikost výkresu oproti skutečné velikosti“ a druhý poměr zní „velikost výkresu oproti skutečné velikosti“.

Pro poměr vlevo používáme poměr, který je na výkresu 10 mm, ale skutečná velikost je 1 stopa.

  • Všimněte si, že velikost výkresu je v čitateli a skutečná velikost ve jmenovateli. Je důležité, aby tyto hodnoty byly pro oba poměry stejné, aby zůstaly stejné.
  • Protože víme, že skutečná velikost soutěžního pole je 11,7 stop (3,2 metru), dosadíme tuto velikost do jmenovatele v druhém poměru.
  • Do čitatele uvedeme velikost soutěžního pole pro výkres, ale tuto velikost zatím neznáme, musíme ji vypočítat. Takže prozatím tam umístíme proměnnou X.

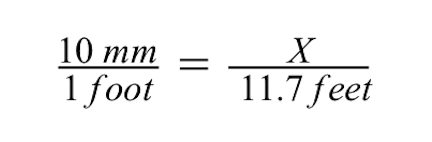
Dva poměry jsou si rovny. První poměr zní „deset milimetrů děleno jednou stopou“ a druhý poměr zní „proměnná X děleno jedenáct celých sedm stop“.

Pro vyřešení X, neznámé výkresové velikosti cihlové budovy, můžeme použít metodu křížového násobení.

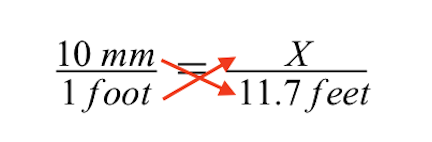
Oba poměry jsou zobrazeny stejně jako dříve, ale nyní jsou zde šipky označující křížové násobení. První poměr opět zní „deset milimetrů děleno jednou stopou“ a druhý poměr zní „proměnná X děleno jedenáct celých sedm stop“.

Použití křížového násobení nám dává následující. Dalším krokem je vyřešit neznámou velikost soutěžního pole označeného X, která je nakreslena.

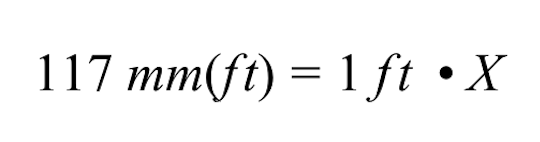
Výsledkem křížového násobení je rovnice „sto sedmnáct milimetrů vynásobených jednou stopou se rovná jedné stopě vynásobené proměnnou X“.

Abychom vyřešili X, musíme vzít zpět násobení 1 stopy krát X vydělením obou stran 1 stopou.

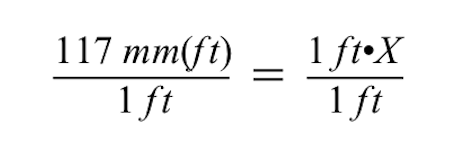
Tato rovnice je podobná té, kterou jsme měli v minulém kroku, ale nyní jsou obě strany děleny jednou stopou. Nyní to zní „sto sedmnáct milimetrů vynásobeno jednou stopou děleno jednou stopou se rovná jedné stopě vynásobené proměnnou X děleno jednou stopou“.

Všimněte si, že při dělení obou stran číslem 1 stopy se jednotky stopy na levé a pravé straně znaménka rovnosti zruší, takže na levé straně zůstanou pouze milimetry (mm).

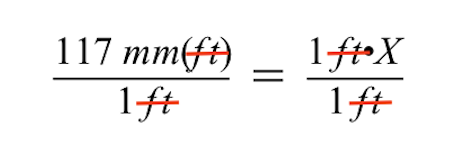
Rovnice je stejná jako v posledním kroku, ale všechny výrazy „noha“ jsou přeškrtnuté. Nyní to zní „sto sedmnáct milimetrů se rovná proměnné X“.

Zjednodušíme-li to dále, vidíme, že pravá strana se redukuje pouze na naši neznámou velikost výkresu soutěžního pole, reprezentovanou proměnnou X.

  • Na levé straně nám zbývá 117 mm. Neznámá velikost kresby soutěžního pole je tedy 117 mm.

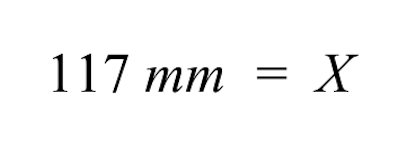
Konečným výsledkem je rovnice definující proměnnou X. Zní: „proměnná X se rovná sto sedmnácti milimetrům“.

Otázka:Obvod vnější strany soutěžního pole je 11,9 x 11,9 stop. Jaké jsou zmenšené rozměry vnější strany hřiště, abyste je mohli přidat do výkresu, který již máte pro interiér?
A:Rozměry jsou 119 mm x 119 mm, přičemž se použije stejný postup jako výše.

Ikona Rozšiřte si učení Rozšiřte si své učení - Zdolávání soutěžního pole

Vytvořte nákres letošního závodiště robotické soutěže VEX v měřítku. Následuje příklad obrázku hřiště Tower Takeover Field pro sezónu 2019-2020, ale obrázky hřiště z aktuálního roku jsou k dispozici na tomto odkazu

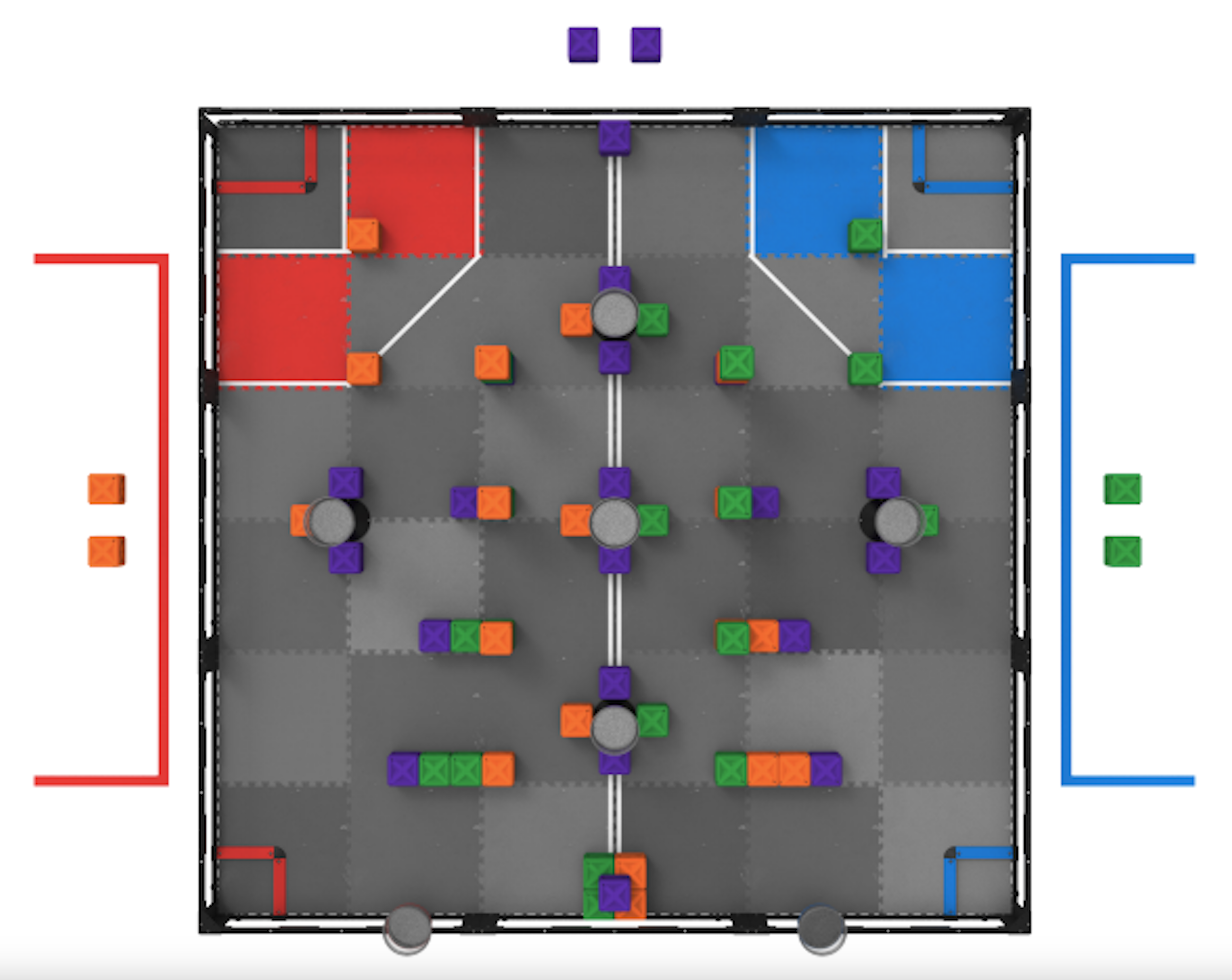
Pohled shora na herní pole Tower Takeover 2019-2020 s válcovými věžemi, krychlemi a stanicemi týmových aliancí.

Začínající studenti mohou použít obrázek soutěžního hřiště, jako je tento, a určit měřítko na základě skutečných rozměrů poskytnutých programem VEX a rozměrů v obrázku.
Zkušení studenti si mohou vytvořit vlastní kresby letošního hřiště v měřítku na základě rozměrů poskytnutých programem VEX.
Pokročilí studenti si mohou vytvořit kresbu hřiště v měřítku a poté iterovat (plánovat, testovat a zdokonalovat) autonomní program.

< Zpět Zpět do laboratoří Další >