"로봇 수학" 의 장점
"로봇 수학"의 장점
비례 추론과 규모와 같은 수학적 개념을 효과적으로 사용하는 로봇 팀은 일반적으로 경쟁에서 우위를 점합니다. 경쟁 중에 이러한 팀이 다른 팀과 동맹을 맺으면 새로운 경로를 계획하거나 자율 프로그램에 대한 올바른 모터 회전 값을 결정하는 등 빠르게 변경할 수 있습니다. 변화의 이면에 있는 수학적 원리를 알면 귀중한 시간을 절약할 수 있습니다. 그런 다음 팀은 그 시간을 이용해 로봇의 물리적 또는 프로그램적 변경을 가해 승리 확률을 높입니다. 비례 추론 및 규모와 같은 "로봇 수학"을 사용하면 확실히 팀의 성과를 극대화할 수 있습니다.
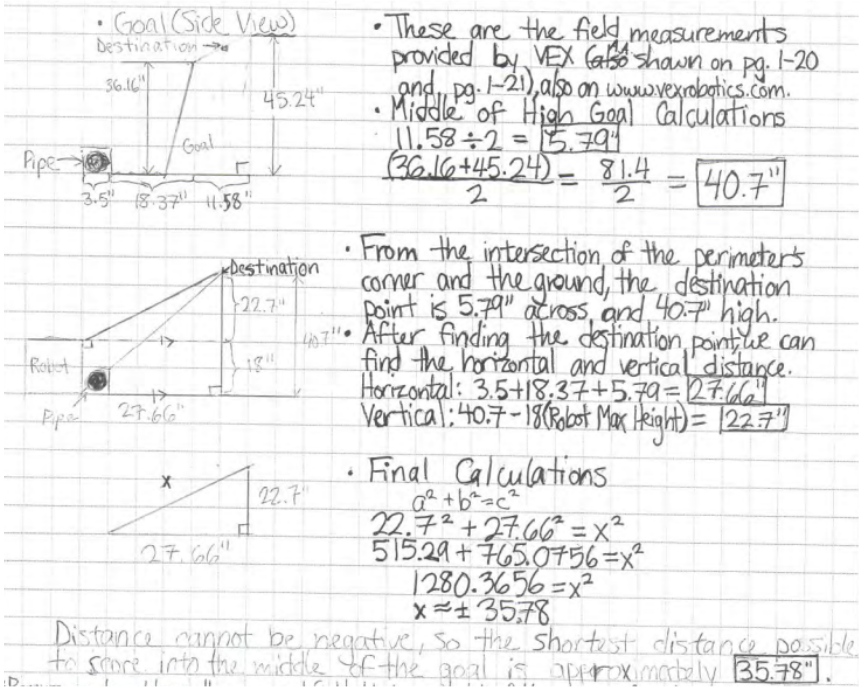
위 이미지에서 팀은 VEX가 제공한 필드의 실제 측정값을 사용하여 필드의 다른 위치 간 거리를 계산합니다. 그런 다음 특정 위치에서 계획된 목적지까지의 가장 짧은 거리를 계산합니다. 이는 자율 프로그램 중에 로봇을 정확하게 움직이는 데 특히 중요한 계산입니다.
![]() 동기 부여 토론
-
수학을 스케일에 적용
동기 부여 토론
-
수학을 스케일에 적용
질문:추측과 확인 대신 "로봇 수학"을 사용하는 이유는 무엇입니까?
답변:추측과 확인에는 시간이 너무 많이 걸립니다. 또한, 로봇이나 프로그램을 조정하는 방법을 결정하기 위해 수학을 사용하면 각각의 새로운 값을 추측하고 확인하는 대신 체계적으로 숫자/값에 변경 사항을 적용할 수 있습니다.
질문:VEX V5 경쟁 필드를 종이에 그리고 있습니다. 실제 크기는 12 x 12피트에 약간 못 미치는데, 필드 내부의 둘레는 11.7 x 11.7피트입니다. 1피트가 10밀리미터(mm)로 표현되도록 크기를 줄이려고 합니다. 도면 크기/실제 크기 비율은 10mm/1피트입니다. 축소된 도면의 치수는 무엇입니까?
A:축소된 치수는 117mm x 117mm입니다.
수학적 설명:
비율은 두 비율이 동일함을 보여줍니다.

왼쪽의 비율의 경우, 도면은 10mm이지만 실제 크기는 1피트라는 비율을 사용합니다.
- 그림의 크기는 분자에 있고 실제 크기는 분모에 있습니다. 두 비율이 동일하게 유지되도록 두 비율을 동일하게 유지하는 것이 중요합니다.
- 실제 경기장의 크기가 11.7피트라는 것을 알고 있으므로 이를 두 번째 비율의 분모에 넣습니다.
- 분자에는 대회 필드의 그림 크기가 들어가지만, 우리는 아직 이 크기를 모르기 때문에 계산해야 합니다. 그럼, 지금은 변수 X를 거기에 두겠습니다.

벽돌 건물의 알려지지 않은 도면 크기 X를 구하기 위해 교차 곱셈 방법을 사용할 수 있습니다.

교차 곱셈을 사용하면 다음과 같은 결과를 얻을 수 있습니다. 다음 단계는 X로 지정된 경쟁 필드의 알려지지 않은 도면 크기를 해결하는 것입니다.

X를 구하려면 1피트에 X를 곱한 값을 원래대로 되돌리려면 양변을 1피트로 나누어야 합니다.

양쪽을 1피트로 나눌 때, 등호의 왼쪽과 오른쪽에서 피트 단위가 상쇄되어 왼쪽에는 밀리미터(mm)만 남는다는 점에 유의하세요.

더 단순화하면, 오른쪽은 경쟁 필드의 알려지지 않은 그림 크기, 즉 변수 X로 표현되는 것으로 축소됩니다.
- 왼쪽에는 117mm가 남습니다. 따라서 대회 필드의 알려지지 않은 도면 크기는 117mm이다.

질문:경기장 외부의 둘레는 11.9 x 11.9피트입니다. 이미 가지고 있는 내부 도면에 추가할 수 있도록 필드 외부의 축소된 치수는 무엇입니까?
A:위와 동일한 과정을 사용하여 치수는 119mm x 119mm입니다.
![]() 학습 확장
-
경쟁 분야 확장
학습 확장
-
경쟁 분야 확장
올해의 VEX 로봇 경연대회 경기장의 축척된 도면을 만드세요. 다음은 2019-2020 타워 테이크오버 필드의 예시 사진이지만, 당해 연도 필드의 이미지는 이 링크에서수 있습니다.

초보 학생은 이와 같은 경쟁 경기장 이미지를 사용하고 VEX에서 제공한 실제 측정값과 이미지 내의 측정값을 기반으로 규모를 파악할 수 있습니다.
숙련된 학생은 VEX에서 제공한 치수를 기반으로 올해 경기장의 축소된 도면을 직접 만들 수 있습니다.
고급 학생은 경기장의 축소된 도면을 만든 다음 자율 프로그램을 반복(계획, 테스트 및 개선)할 수 있습니다.