Skip to main content

“Robot Matematiği” nin Avantajı

Takım mühendisliği not defteri sayfasının sol tarafında hedeflerin ve varış noktalarının taslakları, sağ tarafında ise açıklamalar ve hesaplamalar yer almaktadır. Her diyagram, hesaplamanın amacını ve bunun sonraki adımlara nasıl bilgi sağlayacağını açıklayarak ayrıntılı bir şekilde açıklanmıştır.
Bir ekip, mühendislik not defterlerinde bir rota planlamak için matematiği uygular.

"Robot Matematiğin" Avantajı

Orantılı akıl yürütme ve ölçeklendirme gibi matematiksel kavramları etkili bir şekilde kullanan robotik takımları genellikle yarışmalarda üstünlük sağlar. Bu takımlar yarışma sırasında diğerleriyle ittifaklar kurduklarında, yeni bir yol haritası çizmek veya otonom programları için doğru motor dönüş değerlerini belirlemek gibi değişiklikleri hızla yapabilirler. Değişikliklerin ardındaki matematiği bilmek değerli zaman kazandırabilir. Takımlar daha sonra bu zamanı robotlarında kazanma şanslarını artırabilecek diğer fiziksel veya program değişikliklerini yapmak için kullanırlar. Orantılı akıl yürütme ve ölçekleme gibi "robot matematiği" kullanmak kesinlikle bir ekibin performansını en üst düzeye çıkarabilir.

Yukarıdaki görselde, ekip VEX'in sağladığı alanın gerçek ölçümlerini kullanarak sahadaki farklı konumlar arasındaki mesafeleri hesaplıyor. Daha sonra belirli bir yerden planlanan varış noktasına en kısa mesafeyi hesaplarlar. Bunlar özellikle otonom program sırasında robotun doğru bir şekilde hareket ettirilmesi için önemli hesaplamalardır.

Tartışmayı Motive Et simgesi Tartışmayı Motive Etme - Ölçeğe Matematik Uygulama

S:Tahmin edip kontrol etmek yerine neden "robot matematiği" kullanırsınız?
C:Tahmin etmek ve kontrol etmek çok fazla zaman alır. Ayrıca, robotunuzu veya programını nasıl ayarlayacağınızı belirlemek için matematik kullanırsanız, her yeni değeri tahmin edip kontrol etmek yerine sayılarınıza/değerlerinize sistematik olarak değişiklikler uygulayabilirsiniz.

S:VEX V5 yarışma alanını kağıt üzerinde çiziyorsunuz. Sahanın iç çevresi 11,7x11,7 feet olduğundan gerçek boyutları 12 x 12 feet'in hemen altındadır. Bunu, 1 ayağın 10 milimetre (mm) ile temsil edileceği şekilde küçültmek istersiniz. Çizim boyutu/gerçek boyut oranı 10 mm/1 foot'tur. Küçültülmüş çizimin boyutları nedir?
A:Ölçeklendirilmiş boyutlar 117 mm x 117 mm'dir.

Matematik açıklaması:

Oranlar iki oranın eşit olduğunu gösterir.

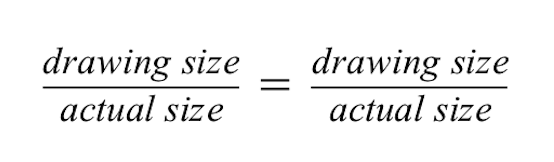
İki oran örneği eşittir. Her iki taraf da birbirinin aynısı. İlk oran 'çizim boyutunun gerçek boyuta oranı', ikinci oran ise 'çizim boyutunun gerçek boyuta oranı' şeklindedir.

Soldaki oran için çizimin 10 mm olduğu ancak gerçek boyutun 1 feet olduğu oranı kullanıyoruz.

  • Çizim boyutunun payda, gerçek boyutun ise paydada olduğunu unutmayın. Her iki oranın da aynı kalması önemlidir, böylece eşit kalırlar.
  • Yarışma alanının gerçek boyutunun 11.7 feet olduğunu bildiğimizden bunu ikinci orandaki paydaya koyacağız.
  • Yarışma alanının çizim ölçüsü paydaya yazılacak ancak bu ölçüyü henüz bilmiyoruz, hesaplamamız gerekiyor. O halde şimdilik X değişkenini oraya koyalım.

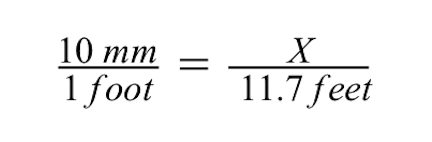
İki oran eşittir. İlk oran 'bir ayakta on milimetre', ikinci oran ise 'on bir nokta yedi ayakta değişken X' olarak okunur.

Tuğla binanın bilinmeyen çizim boyutu olan X'i bulmak için çapraz çarpma yöntemini kullanabiliriz.

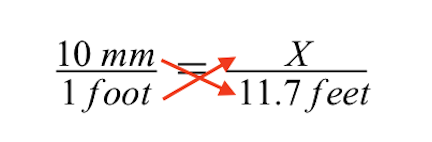
İki oran daha önce gösterildiği gibi aynı şekilde gösteriliyor, ancak artık çapraz çarpımı gösteren oklar var. Yine ilk oran 'bir ayakta on milimetre', ikinci oran ise 'on bir nokta yedi ayakta X değişkeni' olarak okunuyor.

Çapraz çarpımı kullanarak aşağıdaki sonucu elde ederiz. Bir sonraki adım, X ile gösterilen yarışma alanının bilinmeyen çizim boyutunu çözmektir.

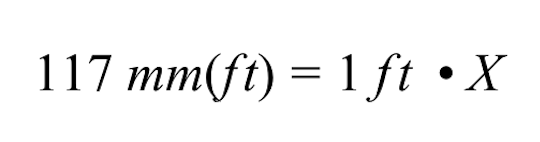
Çarpma işleminin sonucu, 'yüz on yedi milimetre bir ayakla çarpıldığında, bir ayak X değişkeniyle çarpıldığında elde edilen değere eşittir' denklemidir.

X'i bulmak için, 1 feet ile X'in çarpımını her iki tarafı da 1 feet'e bölerek geri almalıyız.

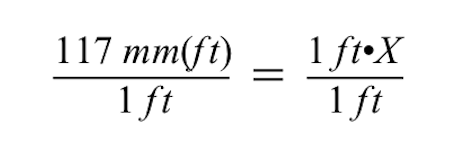
Bu denklem, bir önceki adımda kullandığımız denkleme benziyor, ancak bu sefer her iki taraf da birer feet ile bölünmüş durumda. Şimdi ise 'Yüz on yedi milimetre çarpı bir ayak bölü bir ayak, bir ayak çarpı X değişkeni bölü bir ayakla eşittir' yazıyor.

Her iki tarafı 1 feet'e böldüğünüzde, feet birimlerinin eşitlik işaretinin sol ve sağ taraflarında birbirini götürdüğünü ve sol tarafta sadece milimetre (mm) kaldığını fark edin.

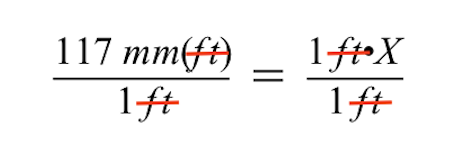
Denklem bir önceki adımla aynıdır, ancak tüm 'ayak' terimleri çizilmiştir. Şimdi 'Yüz on yedi milimetre, X değişkenine eşittir' yazıyor.

Daha da basitleştirdiğimizde, sağ tarafın, yarışma alanının bilinmeyen çizim boyutuna, yani X değişkenine indirgendiğini görüyoruz.

  • Sol tarafta ise 117 mm'lik bir değer kalıyor. Dolayısıyla yarışma alanının bilinmeyen çizim boyutu 117 mm'dir.

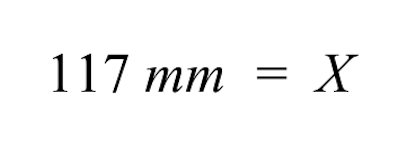
Sonuç olarak X değişkenini tanımlayan bir denklem elde edilir. Denklem şöyle okunur: 'X değişkeni yüz on yedi milimetreye eşittir'.

S:Yarışma alanının dış çevresi 11,9x11,9 feet'tir. Saha dışının küçültülmüş boyutları nelerdir ki bunları iç mekan için zaten elinizde olan çizime ekleyebilesiniz?
A:Yukarıdakiyle aynı işlemi kullanarak boyutlar 119 mm x 119 mm'dir.

Öğrenmenizi Genişletin simgesi Öğreniminizi Genişletin - Rekabet Alanında Ölçeklendirme

Bu yılki VEX Robotik Yarışma Alanının ölçekli çizimini yapın. Aşağıda 2019-2020 Kule Devralma Sahası'nın örnek bir resmi bulunmaktadır ancak mevcut yılın sahasının resimlerine bu.

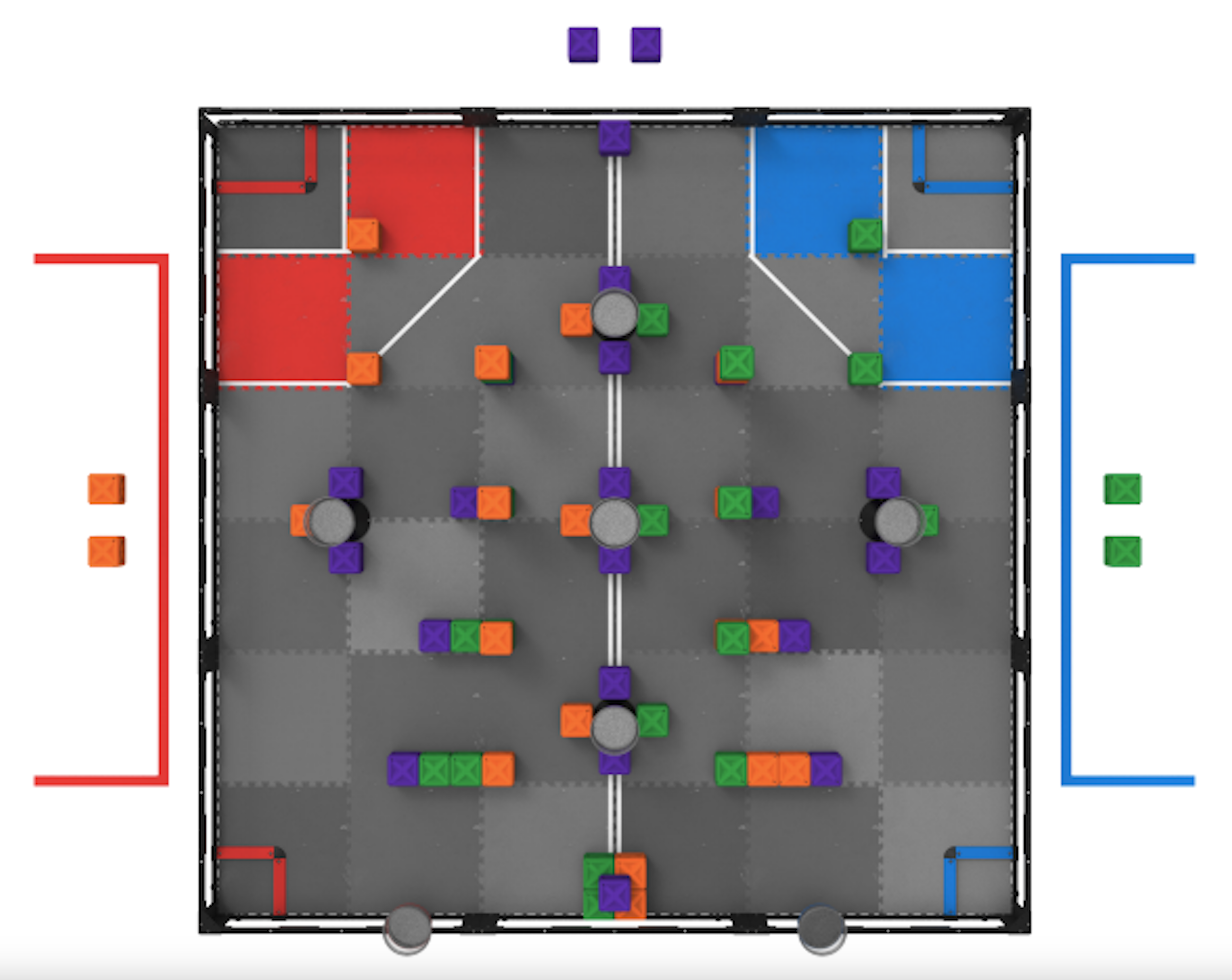
Silindirik kuleler, küpler ve takım ittifak istasyonlarının yer aldığı 2019-2020 Tower Takeover oyun alanının yukarıdan görünümü.

Başlangıç seviyesindeki öğrenciler, buradaki gibi bir yarışma alanı görüntüsü kullanabilir ve VEX tarafından sağlanan gerçek ölçümlere ve görüntüdeki ölçümlere dayanarak ölçeği belirleyebilirler.
Deneyimli öğrenciler, VEX tarafından sağlanan boyutlara dayanarak bu yılki alanın kendi ölçekli çizimlerini oluşturabilirler.
İleri seviyedeki öğrenciler, alanın ölçekli çizimlerini oluşturabilir ve ardından otonom bir programı yineleyebilir (planlayabilir, test edebilir ve iyileştirebilir).

< Geri Laboratuvarlara Dön İleri >