"रोबोट गणित" का लाभ
"रोबोट गणित" का लाभ
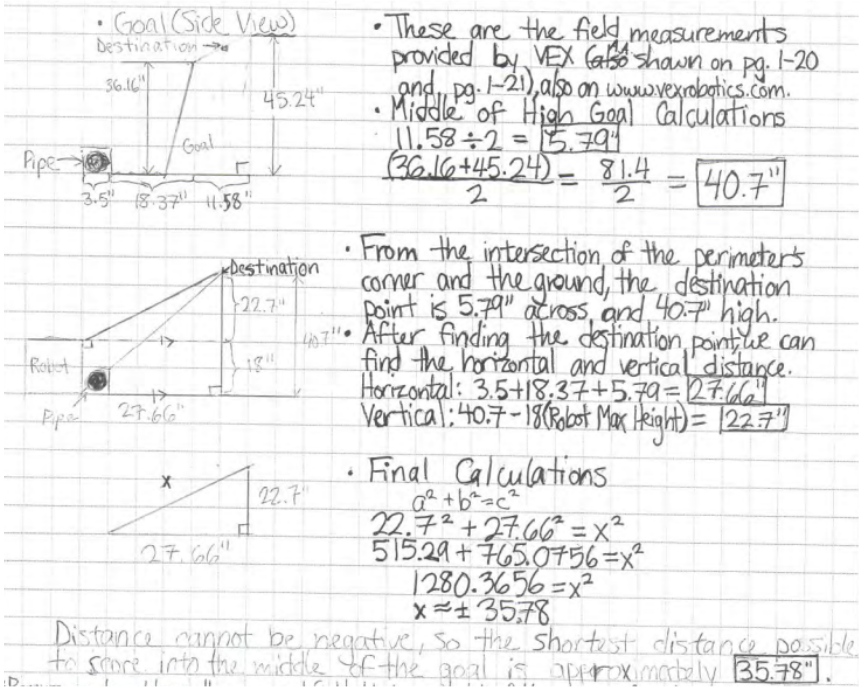
रोबोटिक्स टीमें जो आनुपातिक तर्क और पैमाने जैसी गणितीय अवधारणाओं का प्रभावी ढंग से उपयोग करती हैं, आमतौर पर प्रतियोगिताओं में बढ़त हासिल करती हैं। जब ये टीमें प्रतियोगिता के दौरान दूसरों के साथ गठबंधन बनाती हैं, तो वे तेजी से बदलाव कर सकती हैं, जैसे कि एक नया रास्ता बनाना या अपने स्वायत्त कार्यक्रमों के लिए सही मोटर रोटेशन मान निर्धारित करना। परिवर्तनों के पीछे के गणित को जानने से बहुमूल्य समय की बचत हो सकती है। इसके बाद टीमें उस समय का उपयोग अपने रोबोट में अन्य भौतिक या प्रोग्राम परिवर्तन करने के लिए करती हैं, जिससे उनकी जीत की संभावना बढ़ जाती है। आनुपातिक तर्क और पैमाने जैसे "रोबोट गणित" का उपयोग निश्चित रूप से एक टीम के प्रदर्शन को अधिकतम कर सकता है।
उपरोक्त छवि में, टीम मैदान पर विभिन्न स्थानों के बीच की दूरी की गणना करने के लिए VEX द्वारा प्रदान किए गए क्षेत्र के वास्तविक माप का उपयोग कर रही है। इसके बाद वे किसी विशेष स्थान से नियोजित गंतव्य तक की न्यूनतम दूरी की गणना करते हैं। स्वायत्त कार्यक्रम के दौरान रोबोट को सटीक रूप से चलाने के लिए ये गणनाएं विशेष रूप से महत्वपूर्ण हैं।
![]() चर्चा को प्रेरित करें
-
पैमाने पर गणित का अनुप्रयोग
चर्चा को प्रेरित करें
-
पैमाने पर गणित का अनुप्रयोग
प्रश्न:आप अनुमान लगाने और जाँच करने के बजाय "रोबोट गणित" का उपयोग क्यों करेंगे?
उत्तर:अनुमान लगाने और जाँच करने में बहुत अधिक समय लगता है। इसके अलावा, यदि आप अपने रोबोट या उसके प्रोग्राम को समायोजित करने के तरीके को निर्धारित करने के लिए गणित का उपयोग करते हैं, तो आप प्रत्येक नए मूल्य का अनुमान लगाने और जांचने के बजाय अपने नंबरों/मूल्यों में व्यवस्थित रूप से परिवर्तन लागू कर सकते हैं।
प्रश्न:आप कागज पर VEX V5 प्रतियोगिता क्षेत्र का चित्रण कर रहे हैं। वास्तविक आयाम 12 x 12 फीट से कुछ कम हैं, जबकि मैदान के आंतरिक भाग की परिधि 11.7 x 11.7 फीट है। आप इसे इस प्रकार छोटा करना चाहेंगे कि 1 फुट को 10 मिलीमीटर (मिमी) द्वारा दर्शाया जाए। ड्राइंग का आकार/वास्तविक आकार अनुपात 10 मिमी/1 फुट है। स्केल किए गए ड्राइंग आयाम क्या हैं?
ए:स्केल किए गए आयाम 117 मिमी x 117 मिमी हैं।
गणित स्पष्टीकरण:
अनुपात यह दर्शाता है कि दो अनुपात बराबर हैं।
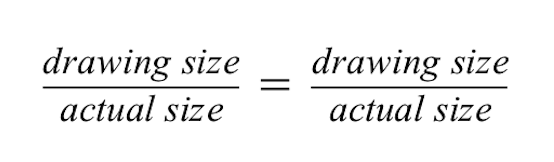
बाईं ओर के अनुपात के लिए, हम उस अनुपात का उपयोग कर रहे हैं जो चित्र में 10 मिमी है लेकिन वास्तविक आकार 1 फुट है।
- ध्यान दें कि ड्राइंग का आकार अंश में है और वास्तविक आकार हर में है। दोनों अनुपातों के लिए इन्हें समान रखना महत्वपूर्ण है ताकि वे बराबर रहें।
- चूंकि हम जानते हैं कि प्रतियोगिता मैदान का वास्तविक आकार 11.7 फीट है, इसलिए हम इसे दूसरे अनुपात में हर में रखेंगे।
- प्रतियोगिता क्षेत्र का ड्राइंग आकार अंश में जाएगा, लेकिन हम अभी तक इस आकार को नहीं जानते हैं, हमें गणना करने की आवश्यकता है। तो, अभी के लिए हम वहां चर X रखेंगे।
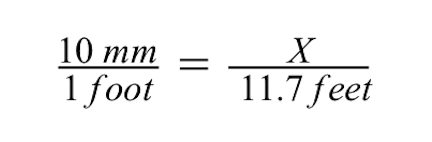
ईंट की इमारत के अज्ञात ड्राइंग आकार X को हल करने के लिए, हम क्रॉस गुणन की विधि का उपयोग कर सकते हैं।
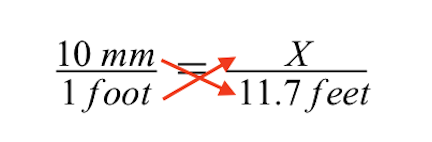
क्रॉस गुणन का उपयोग करने से हमें निम्नलिखित परिणाम प्राप्त होते हैं। अगला चरण X द्वारा निर्दिष्ट प्रतियोगिता क्षेत्र के अज्ञात ड्राइंग आकार को हल करना है।
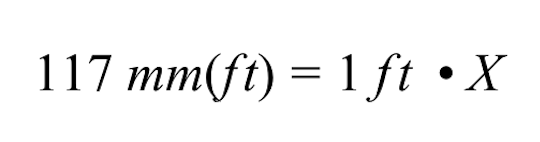
X को हल करने के लिए, हमें 1 फुट गुणा X के गुणनफल को पूर्ववत करना होगा, इसके लिए दोनों पक्षों को 1 फुट से भाग देना होगा।
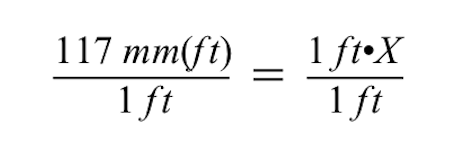
ध्यान दें कि जब दोनों पक्षों को 1 फुट से विभाजित किया जाता है, तो फुट की इकाइयाँ बराबर चिह्न के बाएँ और दाएँ पक्षों पर रद्द हो जाती हैं, तथा बाएँ पक्ष पर केवल मिलीमीटर (मिमी) बचता है।
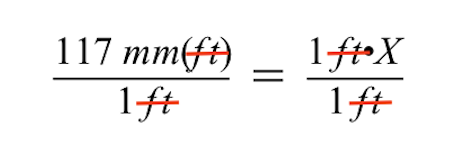
सरलीकरण को और आगे बढ़ाते हुए, हम देखते हैं कि दाहिना भाग प्रतियोगिता क्षेत्र के हमारे अज्ञात आरेख आकार तक सिमट जाता है, जिसे चर X द्वारा दर्शाया जाता है।
- बायीं ओर, हमारे पास 117 मिमी बचती है। इस प्रकार, प्रतियोगिता क्षेत्र का अज्ञात ड्राइंग आकार 117 मिमी है।
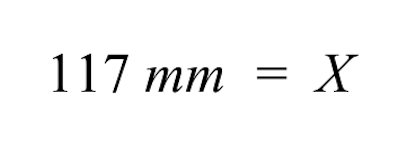
प्रश्न:प्रतियोगिता मैदान के बाहरी भाग की परिधि 11.9 गुणा 11.9 फीट है। मैदान के बाहरी भाग के छोटे आयाम क्या हैं, ताकि आप उन्हें उस चित्र में जोड़ सकें जो आपके पास पहले से ही आंतरिक भाग के लिए है?
A:आयाम 119 मिमी x 119 मिमी हैं, जो ऊपर बताई गई प्रक्रिया का ही उपयोग करते हैं।
![]() अपनी शिक्षा का विस्तार करें
-
प्रतिस्पर्धा क्षेत्र का विस्तार
अपनी शिक्षा का विस्तार करें
-
प्रतिस्पर्धा क्षेत्र का विस्तार
इस वर्ष के VEX रोबोटिक्स प्रतियोगिता क्षेत्र का एक स्केल्ड चित्र बनाएं। निम्नलिखित 2019-2020 टॉवर टेकओवर फ़ील्ड की एक उदाहरण तस्वीर है, लेकिन चालू वर्ष के फ़ील्ड की छवियां इस लिंकपरहैं।
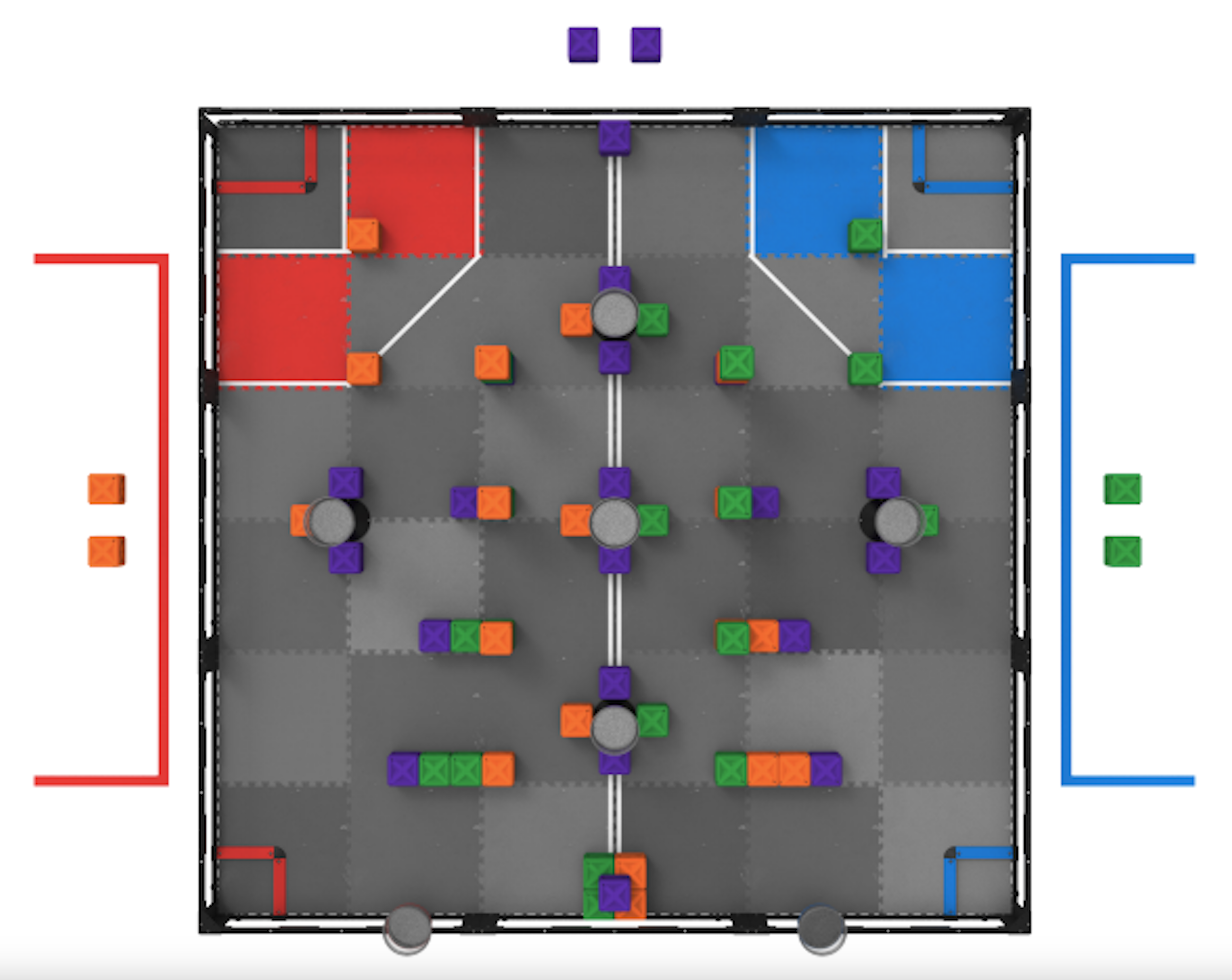
शुरुआती छात्र प्रतियोगिता क्षेत्र की एक छवि का उपयोग कर सकते हैं, जैसे कि यह, और VEX द्वारा प्रदान किए गए वास्तविक मापों और छवि के भीतर के मापों के आधार पर पैमाने का पता लगा सकते हैं।
अनुभवी छात्र VEX द्वारा प्रदान किए गए आयामों के आधार पर इस वर्ष के क्षेत्र के अपने स्वयं के स्केल किए गए चित्र बना सकते हैं।
उन्नत छात्र क्षेत्र का अपना स्केल किया गया चित्र बना सकते हैं और फिर एक स्वायत्त कार्यक्रम को दोहरा सकते हैं (योजना, परीक्षण और परिष्कृत कर सकते हैं)।