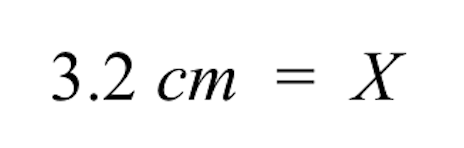Skip to main content

Pochopení měřítka

Ikona sady nástrojů pro učitele Sada nástrojů této stránky

Účelem této stránky je poskytnout studentům procvičení a kontext pro škálování, které budou muset dokončit v rámci předmětu Návrh a škálování závodní dráhy a později v soutěži Robo Rally Challenge.

Zapojte studenty do diskuse s celou třídou, aby si zopakovali otázky z motivačního programu. Požádejte studenty, aby si svou práci a myšlenky zapsali do svého technického sešitu.

Kreslená mapa světa s překrytím mřížky měřítka a pravítkem symbolizujícím koncept měřítka.
Používání stupnice je důležitá dovednost, kterou se musíte naučit.

Co je „Měřítko“?

Měřítko je vztah nebo poměr mezi nastavenou vzdáleností na mapě nebo kresbě a jejími odpovídajícími vzdálenostmi v reálném životě. Materiály, které používají měřítko, jako jsou plány, jsou často považovány za cennější, protože umožňují uživateli vnímat vzdálenost vizuálně, což z nich činí efektivnější modely. Schopnost převádět měření při práci s měřítkem je důležitá pro kariéru, která zahrnuje mapy, plány a architektonické modely. Profesionálové jako architekti, inženýři, vojáci a scénografové všichni ve svém oboru nějakým způsobem používají měřítko.

Vypracování podrobného náčrtu jako plánu je důležitým krokem v procesu inženýrského návrhu. Když vytváříme zmenšenou kopii objektu, originál a kopie musí mít stejné proporce. K prezentaci toho, jak moc byl objekt skutečně zmenšen (nebo nahoru), často používáme poměry. Tyto poměry jsou zobrazeny na zmenšené kopii, aby mohl být objekt v reálném životě správně reprezentován. Například měřítko na výkresu může být znázorněno jako 1 cm = 20 m. Díky tomu tým ví, že na každý 1 cm náčrtu je reálné měření 20 m. Pokud je tedy stěna na náčrtu zobrazena jako 4 cm, musí být skutečná stěna 80 m. Když inženýři staví věci, jako jsou dálnice nebo budovy, škálované plány jsou průběžně kontrolovány, aby se ujistili, že proporce jsou vždy správné. Rozdělení reálného modelu do sekcí a kontrola správných proporcí při vyplňování každé sekce je jedním ze způsobů, jak týmy pracují, aby se ujistily, že se udržují v měřítku. Chyby mohou způsobit ztrátu značného množství času, peněz a materiálu, takže dodržování přesnosti váhy je zásadní.

Ikona motivační diskuse Motivovat diskusi

Škálování může být pro některé studenty obtížné. Místo toho, aby studenti procvičovali a opakovali matematické postupy, uspořádejte diskusi, aby mohli studenti spolužákům vysvětlit, jak uvažují o škálování.
Otázka:Červená budova na kresbě města je vysoká 2 centimetry, ale ve skutečnosti je vysoká 50 metrů. Šedá budova vedle na obrázku je vysoká pouze 1 centimetr. Jak vysoká je ve skutečnosti ta další budova?
A:Ve skutečnosti je vysoká 25 metrů. Viz vysvětlení níže:

Poměry ukazují, že dva poměry jsou si rovny.

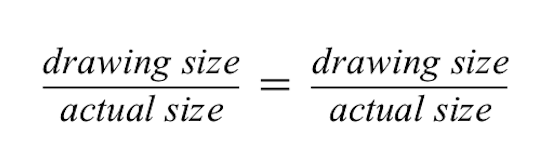
Dva příklady poměrů jsou si rovny. Každá strana je identická. První poměr zní „velikost výkresu oproti skutečné velikosti“ a druhý poměr zní „velikost výkresu oproti skutečné velikosti“.

Pro poměr vlevo víme, že kresba červené budovy je 2 cm vysoká, ale skutečná velikost červené budovy je 50 metrů.

  • Všimněte si, že velikost výkresu je v čitateli a skutečná velikost ve jmenovateli. Je důležité, aby tyto hodnoty byly pro oba poměry stejné, aby zůstaly stejné.
  • Protože víme, že velikost výkresu šedé budovy je 1 cm, dosadíme to do čitatele ve druhém poměru.
  • Skutečná velikost šedé budovy půjde do jmenovatele, ale tuto velikost zatím neznáme, musíme ji vypočítat. Takže prozatím tam umístíme proměnnou X.

Dva poměry jsou si rovny. První poměr zní „dva centimetry děleno padesáti metry“ a druhý poměr zní „jeden centimetr děleno proměnnou X“.

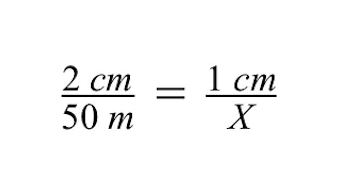
Pro vyřešení proměnné X, neznámé skutečné velikosti šedé budovy, můžeme použít metodu křížového násobení.

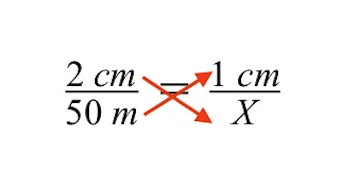
Oba poměry jsou zobrazeny stejně jako dříve, ale nyní jsou zde šipky označující křížové násobení. První poměr opět zní „dva centimetry děleno padesáti metry“ a druhý poměr „jeden centimetr děleno proměnnou X“.

Použití křížového násobení nám dává následující. Dalším krokem je vyřešit neznámou velikost šedé budovy určenou proměnnou X.

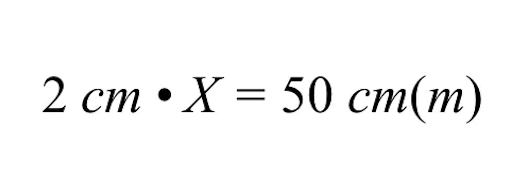
Výsledkem křížového násobení je rovnice „dva centimetry vynásobené proměnnou X se rovnají padesáti centimetrům vynásobeným jedním metrem“.

Abychom vyřešili X, musíme vrátit zpět násobení 2 cm a proměnné X tak, že obě strany rovnice vydělíme 2 cm.

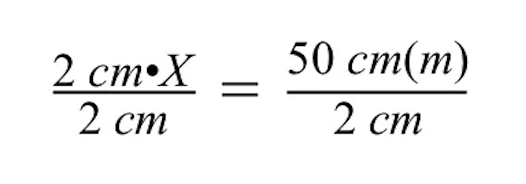
Tato rovnice je podobná té, kterou jsme měli v minulém kroku, ale nyní jsou obě strany děleny dvěma centimetry. Nyní to zní „dva centimetry vynásobené proměnnou X dělené dvěma centimetry se rovnají padesáti centimetrům vynásobeným jedním metrem děleným dvěma centimetry“.

Všimněte si, že při dělení obou stran 2 cm se jednotky cm na levé a pravé straně znaménka rovnosti zruší, takže na pravé straně zůstanou pouze metry (m).

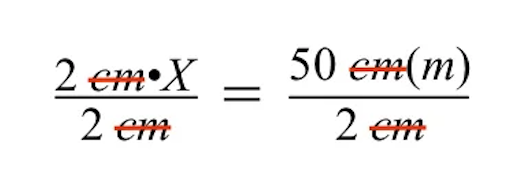
Rovnice je stejná jako v posledním kroku, ale všechny členy označující „centimetr“ jsou přeškrtnuté. Nyní to zní „dva vynásobené proměnnou X děleno dvěma se rovná padesáti metrům děleno dvěma“.

Zjednodušíme-li to dále, vidíme, že levá strana se zmenšuje na naši neznámou skutečnou velikost šedé budovy, reprezentovanou proměnnou X.

  • Na pravé straně nám zbývá 25 m. Neznámá skutečná velikost šedé budovy je tedy 25 m.
  • To je rozumné, protože pokud 2 cm pro velikost výkresu odpovídají 50 metrům pro skutečnou velikost, pak by poloviční zmenšení o 1 cm mělo znamenat 25 metrů.

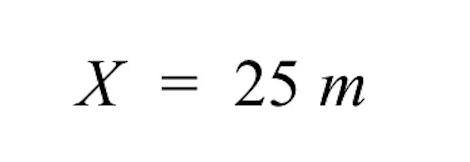
Konečným výsledkem je rovnice definující proměnnou X. Zní: „proměnná X se rovná dvaceti pěti metrům“.

Otázka:Co kdybychom chtěli do výkresu přidat cihlovou budovu, která je ve skutečnosti vysoká 80 metrů? Kolik centimetrů by to mělo být?
A:3,2 centimetru. Viz vysvětlení níže:

Proporce ukazují, že oba poměry jsou si rovny.

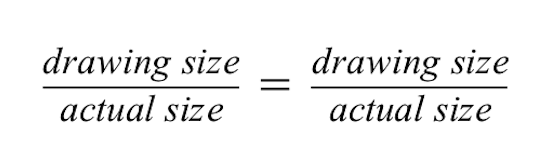
Dva příklady poměrů jsou si rovny. Každá strana je identická. První poměr zní „velikost výkresu oproti skutečné velikosti“ a druhý poměr zní „velikost výkresu oproti skutečné velikosti“.

Pro poměr vlevo víme, že kresba červené budovy je 2 cm vysoká, ale skutečná velikost červené budovy je 50 metrů.

  • Všimněte si, že velikost výkresu je v čitateli a skutečná velikost ve jmenovateli. Je důležité, aby tyto hodnoty byly pro oba poměry stejné, aby zůstaly stejné.
  • Protože víme, že velikost výkresu šedé budovy je 1 cm, dosadíme to do čitatele ve druhém poměru.
  • Skutečná velikost šedé budovy půjde do jmenovatele, ale tuto velikost zatím neznáme, musíme ji vypočítat. Takže prozatím tam umístíme proměnnou X.

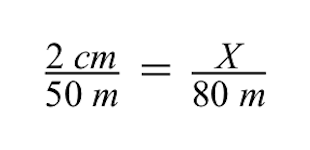
Dva poměry jsou si rovny. První poměr zní „dva centimetry děleno padesát metrů“ a druhý poměr zní „proměnná X děleno osmdesát metrů“.

Pro vyřešení proměnné X, neznámé rozměry výkresu cihlové budovy, můžeme použít metodu křížového násobení.

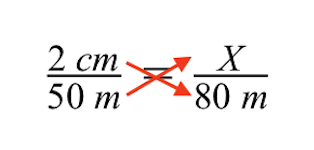
Oba poměry jsou zobrazeny stejně jako dříve, ale nyní jsou zde šipky označující křížové násobení. První poměr opět zní „dva centimetry děleno padesát metrů“ a druhý poměr „proměnná X děleno osmdesát metrů“.

Použití křížového násobení nám dává následující. Dalším krokem je vyřešit neznámou velikost šedé budovy určenou proměnnou X.

Výsledkem křížového násobení je rovnice „sto šedesát centimetrů vynásobených jedním metrem se rovná padesáti metrům vynásobeným proměnnou X“.

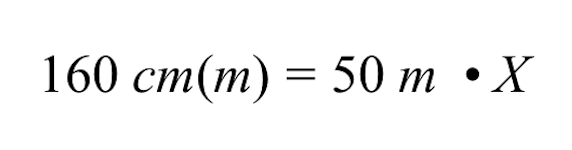
Abychom vyřešili proměnnou X, musíme vrátit zpět násobení 50 m krát X vydělením obou stran číslem 50 m.

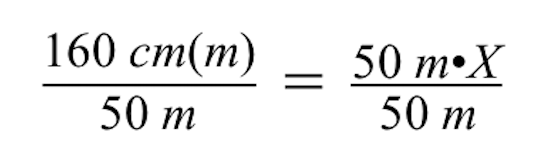
Tato rovnice je podobná té, kterou jsme měli v minulém kroku, ale nyní jsou obě strany děleny padesáti metry. Nyní to zní „sto šedesát centimetrů vynásobeno jedním metrem děleno padesáti metry se rovná padesáti metrům vynásobeným proměnnou X děleno padesáti metry“.

Všimněte si, že při dělení obou stran číslem 50 m se jednotky m (metry) na levé a pravé straně znaménka rovnosti zruší, takže na levé straně zůstanou pouze centimetry (cm).

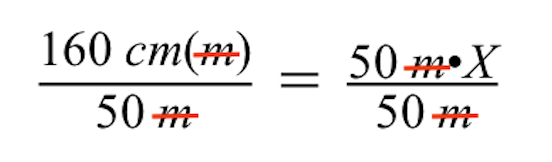
Rovnice je stejná jako v posledním kroku, ale všechny členy „metru“ jsou přeškrtnuté. Nyní to zní „sto šedesát centimetrů děleno padesáti se rovná padesáti vynásobeným proměnnou X děleno padesáti“.

Při dalším zjednodušení vidíme, že se pravá strana zmenšuje pouze na naši neznámou velikost výkresu cihlové budovy, reprezentovanou proměnnou X.

  • Na levé straně nám zbývá 3,2 cm. Neznámá velikost kresby cihlové budovy je tedy 3,2 cm.

Konečným výsledkem je rovnice definující proměnnou X. Zní: „proměnná X se rovná třem celým dvěma centimetrům“.

< Zpět Zpět do laboratoří Další >