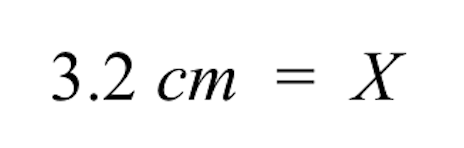സ്കെയിൽ മനസ്സിലാക്കൽ

ഒരു റേസ് കോഴ്‌സ് ഡിസൈനിംഗ് ആൻഡ് സ്കെയിലിംഗ്, തുടർന്ന് റോബോ റാലി ചലഞ്ച് എന്നിവയിൽ വിദ്യാർത്ഥികൾ പൂർത്തിയാക്കേണ്ട സ്കെയിലിംഗിനുള്ള പരിശീലനവും സന്ദർഭവും നൽകുക എന്നതാണ് ഈ പേജിന്റെ ലക്ഷ്യം.

മോട്ടിവേറ്റ് ചർച്ച ചോദ്യങ്ങൾ അവലോകനം ചെയ്യുന്നതിനായി വിദ്യാർത്ഥികളെ മുഴുവൻ ക്ലാസ് ചർച്ചയിൽ ഉൾപ്പെടുത്തുക. വിദ്യാർത്ഥികളോട് അവരുടെ എഞ്ചിനീയറിംഗ് നോട്ട്ബുക്കിൽ അവരുടെ കൃതികളും ചിന്തകളും എഴുതാൻ ആവശ്യപ്പെടുക.

ചില വിദ്യാർത്ഥികൾക്ക് പ്രയോഗിക്കാൻ ബുദ്ധിമുട്ടുള്ള ഒരു ആശയമാണ് സ്കെയിലിംഗ്. വിദ്യാർത്ഥികളെക്കൊണ്ട് ഗണിതശാസ്ത്രം ഡ്രിൽ ചെയ്ത് പരിശീലിപ്പിക്കുന്നതിന് പകരം, സ്കെയിലിംഗിനെക്കുറിച്ച് സഹപാഠികൾക്ക് എങ്ങനെ ന്യായവാദം ചെയ്യാമെന്ന് വിശദീകരിക്കാൻ ഒരു ചർച്ച നടത്തുക.
ചോദ്യം:നഗരത്തിലെ ഒരു ചിത്രത്തിലെ ഒരു ചുവന്ന കെട്ടിടത്തിന് 2 സെന്റീമീറ്റർ ഉയരമുണ്ട്, പക്ഷേ അത് യഥാർത്ഥത്തിൽ 50 മീറ്ററാണ് ഉയരം. ഡ്രോയിംഗിൽ അതിനടുത്തുള്ള ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന് 1 സെന്റീമീറ്റർ ഉയരമേ ഉള്ളൂ. അടുത്ത കെട്ടിടത്തിന് ശരിക്കും എത്ര ഉയരമുണ്ട്?
എ:ഇതിന് ശരിക്കും 25 മീറ്റർ ഉയരമുണ്ട്. താഴെയുള്ള വിശദീകരണം കാണുക:

അനുപാതങ്ങൾ രണ്ട് അനുപാതങ്ങളും തുല്യമാണെന്ന് കാണിക്കുന്നു.

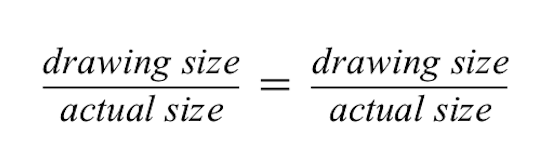
ഇടതുവശത്തുള്ള അനുപാതത്തിന്, ചുവന്ന കെട്ടിടത്തിന്റെ ഡ്രോയിംഗിന് 2 സെ.മീ ഉയരമുണ്ടെന്ന് നമുക്കറിയാം, പക്ഷേ ചുവന്ന കെട്ടിടത്തിന്റെ യഥാർത്ഥ വലുപ്പം 50 മീറ്ററാണ്.

• ഡ്രോയിംഗിന്റെ വലുപ്പം ന്യൂമറേറ്ററിലും യഥാർത്ഥ വലുപ്പം ഡിനോമിനേറ്ററിലും ആണെന്ന് ശ്രദ്ധിക്കുക. രണ്ട് അനുപാതങ്ങളും തുല്യമായി നിലനിർത്തുന്നതിന് ഇവ ഒരേപോലെ നിലനിർത്തേണ്ടത് പ്രധാനമാണ്.
• ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ ഡ്രോയിംഗ് വലുപ്പം 1 സെന്റീമീറ്റർ ആണെന്ന് നമുക്കറിയാവുന്നതിനാൽ, രണ്ടാമത്തെ അനുപാതത്തിലെ ന്യൂമറേറ്ററിൽ ഇത് ഇടും.
• ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ യഥാർത്ഥ വലുപ്പം ഡിനോമിനേറ്ററിൽ ഉൾപ്പെടുത്തും, പക്ഷേ ഈ വലുപ്പം ഞങ്ങൾക്ക് ഇതുവരെ അറിയില്ല, നമ്മൾ കണക്കാക്കേണ്ടതുണ്ട്. അപ്പോൾ, ഇപ്പോൾ നമുക്ക് വേരിയബിൾ X അവിടെ ഇടാം.

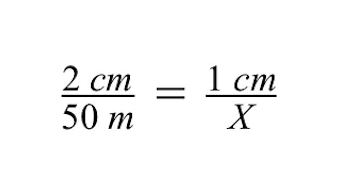
ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ അജ്ഞാതമായ യഥാർത്ഥ വലുപ്പമായ വേരിയബിൾ X പരിഹരിക്കുന്നതിന്, നമുക്ക് ക്രോസ് ഗുണന രീതി ഉപയോഗിക്കാം.

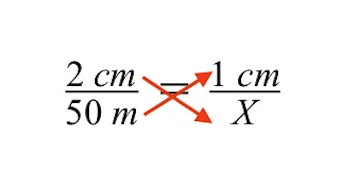
ക്രോസ് ഗുണനം ഉപയോഗിക്കുന്നത് നമുക്ക് ഇനിപ്പറയുന്നവ നൽകുന്നു. അടുത്ത ഘട്ടം, വേരിയബിൾ X സൂചിപ്പിക്കുന്ന ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ അജ്ഞാത വലുപ്പം കണ്ടെത്തുക എന്നതാണ്.

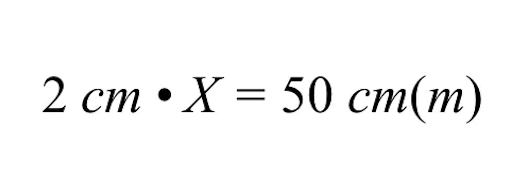
X ന് പരിഹാരം കണ്ടെത്താൻ, നമ്മൾ വേരിയബിൾ X നെ 2 cm ഗുണിച്ച് സമവാക്യത്തിന്റെ ഇരുവശങ്ങളെയും 2 cm കൊണ്ട് ഹരിച്ചാൽ ഗുണിക്കുന്നത് പഴയപടിയാക്കണം.

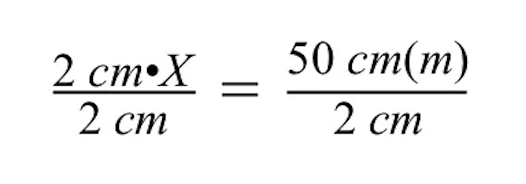
ഇരുവശങ്ങളെയും 2 സെ.മീ കൊണ്ട് ഹരിക്കുമ്പോൾ, തുല്യ ചിഹ്നത്തിന്റെ ഇടതുവശത്തും വലതുവശത്തും സെ.മീയുടെ യൂണിറ്റുകൾ റദ്ദാക്കപ്പെടുന്നു, വലതുവശത്ത് മീറ്ററുകൾ (മീ) മാത്രം അവശേഷിപ്പിക്കുന്നു.

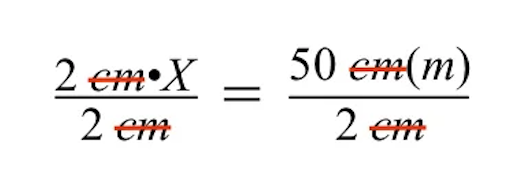
കൂടുതൽ ലളിതമാക്കിയാൽ, ഇടതുവശം ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ നമ്മുടെ അജ്ഞാതമായ യഥാർത്ഥ വലുപ്പത്തിലേക്ക് ചുരുങ്ങുന്നത് നമുക്ക് കാണാം, ഇത് വേരിയബിൾ X പ്രതിനിധീകരിക്കുന്നു.

• വലതുവശത്ത്, നമുക്ക് 25 മീറ്റർ മാത്രമേ ശേഷിക്കുന്നുള്ളൂ. അങ്ങനെ, ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ അജ്ഞാതമായ യഥാർത്ഥ വലിപ്പം 25 മീ.
• ഇത് ന്യായമാണ്, കാരണം ഡ്രോയിംഗ് വലുപ്പത്തിന് 2 സെന്റീമീറ്റർ യഥാർത്ഥ വലുപ്പത്തിന് 50 മീറ്ററിന് ആനുപാതികമാണെങ്കിൽ, 1 സെന്റിമീറ്ററിന് അത് പകുതിയായി മുറിക്കുന്നത് 25 മീറ്ററിന് തുല്യമായിരിക്കണം.

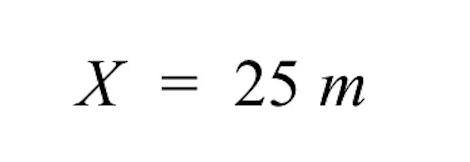
ചോദ്യം:ഡ്രോയിംഗിനൊപ്പം 80 മീറ്റർ ഉയരമുള്ള ഒരു ഇഷ്ടിക കെട്ടിടം കൂടി ചേർക്കാൻ നമ്മൾ ആഗ്രഹിച്ചാലോ? എത്ര സെന്റീമീറ്റർ ആയിരിക്കണം?
എ:3.2 സെന്റീമീറ്റർ. താഴെയുള്ള വിശദീകരണം കാണുക:

അനുപാതങ്ങൾ രണ്ട് അനുപാതങ്ങളും തുല്യമാണെന്ന് കാണിക്കുന്നു.

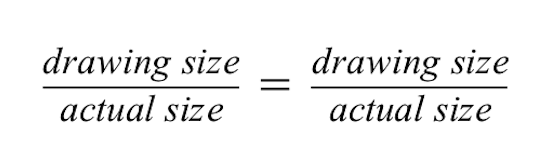
ഇടതുവശത്തുള്ള അനുപാതത്തിന്, ചുവന്ന കെട്ടിടത്തിന്റെ ഡ്രോയിംഗിന് 2 സെ.മീ ഉയരമുണ്ടെന്ന് നമുക്കറിയാം, പക്ഷേ ചുവന്ന കെട്ടിടത്തിന്റെ യഥാർത്ഥ വലുപ്പം 50 മീറ്ററാണ്.

• ഡ്രോയിംഗിന്റെ വലുപ്പം ന്യൂമറേറ്ററിലും യഥാർത്ഥ വലുപ്പം ഡിനോമിനേറ്ററിലും ആണെന്ന് ശ്രദ്ധിക്കുക. രണ്ട് അനുപാതങ്ങളും തുല്യമായി നിലനിർത്തുന്നതിന് ഇവ ഒരേപോലെ നിലനിർത്തേണ്ടത് പ്രധാനമാണ്.
• ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ ഡ്രോയിംഗ് വലുപ്പം 1 സെന്റീമീറ്റർ ആണെന്ന് നമുക്കറിയാവുന്നതിനാൽ, രണ്ടാമത്തെ അനുപാതത്തിലെ ന്യൂമറേറ്ററിൽ ഇത് ഇടും.
• ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ യഥാർത്ഥ വലുപ്പം ഡിനോമിനേറ്ററിൽ ഉൾപ്പെടുത്തും, പക്ഷേ ഈ വലുപ്പം ഞങ്ങൾക്ക് ഇതുവരെ അറിയില്ല, നമ്മൾ കണക്കാക്കേണ്ടതുണ്ട്. അപ്പോൾ, ഇപ്പോൾ നമുക്ക് വേരിയബിൾ X അവിടെ ഇടാം.

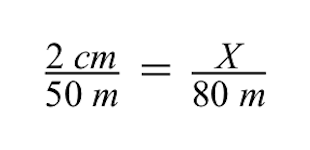
ഇഷ്ടിക കെട്ടിടത്തിന്റെ അജ്ഞാത ഡ്രോയിംഗ് വലുപ്പമായ വേരിയബിൾ X പരിഹരിക്കുന്നതിന്, നമുക്ക് ക്രോസ് ഗുണന രീതി ഉപയോഗിക്കാം.

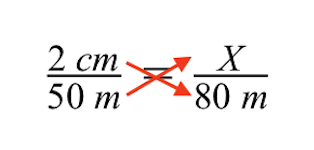
ക്രോസ് ഗുണനം ഉപയോഗിക്കുന്നത് നമുക്ക് ഇനിപ്പറയുന്നവ നൽകുന്നു. അടുത്ത ഘട്ടം, വേരിയബിൾ X സൂചിപ്പിക്കുന്ന ചാരനിറത്തിലുള്ള കെട്ടിടത്തിന്റെ അജ്ഞാത വലുപ്പം കണ്ടെത്തുക എന്നതാണ്.

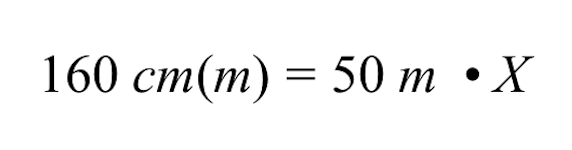
X എന്ന വേരിയബിളിനുള്ള പരിഹാരം കണ്ടെത്താൻ, 50 m ഗുണിത X ന്റെ ഇരുവശങ്ങളെയും 50 m കൊണ്ട് ഹരിച്ചാൽ ഗുണനം പഴയപടിയാക്കണം.

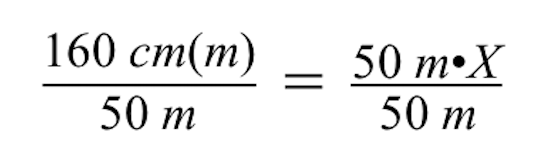
ഇരുവശങ്ങളെയും 50 മീറ്റർ കൊണ്ട് ഹരിക്കുമ്പോൾ, തുല്യ ചിഹ്നത്തിന്റെ ഇടതുവശത്തും വലതുവശത്തും m (മീറ്റർ) ന്റെ യൂണിറ്റുകൾ റദ്ദാക്കപ്പെടുന്നു, ഇടതുവശത്ത് സെന്റീമീറ്ററുകൾ (cm) മാത്രം അവശേഷിപ്പിക്കുന്നു.

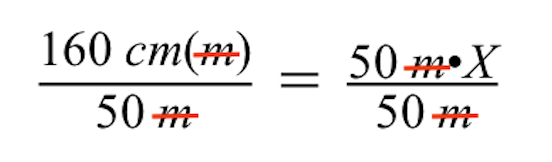
കൂടുതൽ ലളിതമാക്കിയാൽ, വലതുവശം ഇഷ്ടിക കെട്ടിടത്തിന്റെ നമ്മുടെ അജ്ഞാത ഡ്രോയിംഗ് വലുപ്പത്തിലേക്ക് ചുരുങ്ങുന്നത് കാണാം, ഇത് വേരിയബിൾ X കൊണ്ട് പ്രതിനിധീകരിക്കുന്നു.

• ഇടതുവശത്ത്, നമുക്ക് 3.2 സെന്റീമീറ്റർ ശേഷിക്കുന്നു. അങ്ങനെ, ഇഷ്ടിക കെട്ടിടത്തിന്റെ അജ്ഞാത ഡ്രോയിംഗ് വലുപ്പം 3.2 സെന്റീമീറ്റർ ആണ്.