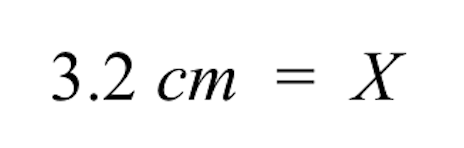Ölçeği Anlamak
![]() Öğretmen Araç Kutusu
-
Bu Sayfanın Amacı
Öğretmen Araç Kutusu
-
Bu Sayfanın Amacı
Bu sayfanın amacı, öğrencilerin Yarış Pisti Tasarlama ve Ölçeklendirme ve daha sonra Robo Ralli Mücadelesi'nde tamamlamaları gereken ölçeklendirme için uygulama ve bağlam sağlamaktır.
Öğrencileri, Motive Edici Tartışma sorularını gözden geçirmek için tüm sınıfın katıldığı bir tartışmaya dahil edin. Öğrencilerden çalışmalarını ve düşüncelerini mühendislik defterlerine yazmalarını isteyin.
 Ölçeği
Ölçeği "Ölçek" nedir?
Ölçek, bir harita veya çizim üzerindeki belirli bir mesafe ile gerçek hayattaki karşılık gelen mesafeleri arasındaki ilişki veya orandır. Taslaklar gibi ölçek kullanan malzemeler, kullanıcının mesafeyi görsel olarak algılamasına izin verdikleri için genellikle daha değerli olarak kabul edilir, bu nedenle onları daha etkili modeller haline getirir. Ölçekle çalışırken ölçümleri dönüştürebilmek, haritaları, planları ve mimari modelleri içeren kariyerler için önemlidir. Mimarlar, mühendisler, askerler ve set tasarımcıları gibi profesyonellerin hepsi sektörlerinde bir şekilde ölçek kullanırlar.
Ayrıntılı bir taslağı plan olarak geliştirmek, mühendislik tasarım sürecinde önemli bir adımdır. Bir nesnenin ölçeklendirilmiş bir kopyasını oluşturduğumuzda, orijinal ve kopya aynı oranlara sahip olmalıdır. Bir nesnenin gerçekte ne kadar küçültüldüğünü (veya yükseltildiğini) göstermek için genellikle oranları kullanırız. Bu oranlar, gerçek hayattaki nesnenin doğru bir şekilde temsil edilebilmesi için ölçeklendirilmiş kopyada görüntülenir. Örneğin, bir çizim üzerindeki bir ölçek 1 cm = 20 m olarak gösterilebilir. Bu, bir ekibin eskizdeki her 1 cm için gerçek hayat ölçümünün 20 m olduğunu bilmesini sağlar. Bu nedenle, kroki üzerinde bir duvar 4 cm olarak temsil ediliyorsa, gerçek hayattaki duvarın 80 m olması gerekir. Mühendisler otoyollar veya binalar gibi şeyler inşa ettiklerinde, oranların her zaman doğru olduğundan emin olmak için ölçekli planlar sürekli olarak kontrol edilir. Gerçek hayattaki modeli bölümlere ayırmak ve her bölümü tamamlarken oranların doğru olup olmadığını kontrol etmek, ekiplerin ölçeklendirmeye devam ettiklerinden emin olmak için çalışmanın bir yoludur. Hatalar önemli ölçüde zaman, para ve malzeme kaybına neden olabilir, bu nedenle ölçeğin doğruluğunu korumak esastır.
![]() Tartışmayı Motive Edin
Tartışmayı Motive Edin
Ölçekleme bazı öğrenciler için uygulanması zor bir kavram olabilir. Öğrencilerin matematikle ilgili alıştırmalar yapıp pratik yapmalarını sağlamak yerine, öğrencilerin ölçekleme konusunda nasıl akıl yürüttüklerini sınıf arkadaşlarına açıklayabilecekleri bir tartışma ortamı yaratın.
S:Şehrin çizimindeki kırmızı bina 2 santimetre yüksekliğindedir ancak gerçekte 50 metre yüksekliğindedir. Çizimde yanındaki gri bina sadece 1 santim yüksekliğinde. Şu yandaki bina gerçekte ne kadar yüksek?
A:Gerçekten 25 metre yüksekliğinde. Aşağıdaki açıklamayı inceleyin:
Oranlar iki oranın eşit olduğunu gösterir.
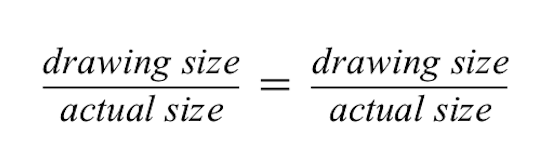
Soldaki oran için kırmızı binanın çiziminin 2 cm boyunda olduğunu ancak kırmızı binanın gerçek boyutunun 50 metre olduğunu biliyoruz.
- Çizim boyutunun payda, gerçek boyutun ise paydada olduğunu unutmayın. Her iki oranın da aynı kalması önemlidir, böylece eşit kalırlar.
- Gri binanın çizim boyutunun 1 cm olduğunu bildiğimizden bunu ikinci orandaki paya koyacağız.
- Paydaya gri binanın gerçek büyüklüğü girecek ancak bu büyüklüğü henüz bilmiyoruz, hesaplamamız gerekiyor. O halde şimdilik X değişkenini oraya koyalım.
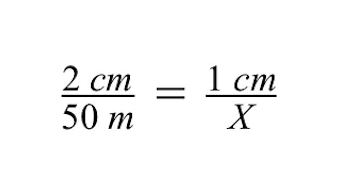
Gri binanın bilinmeyen gerçek büyüklüğü olan X değişkenini çözmek için çapraz çarpma yöntemini kullanabiliriz.
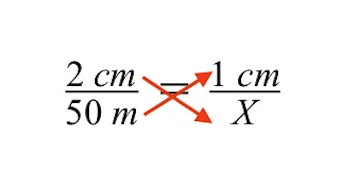
Çapraz çarpımı kullanarak aşağıdaki sonucu elde ederiz. Bir sonraki adım, X değişkeni ile gösterilen gri binanın bilinmeyen boyutunu çözmektir.
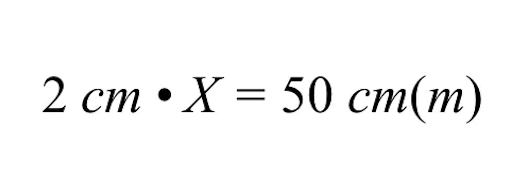
X'i bulmak için, denklemin her iki tarafını 2 cm'ye bölerek 2 cm ile X değişkeninin çarpımını geri almalıyız.
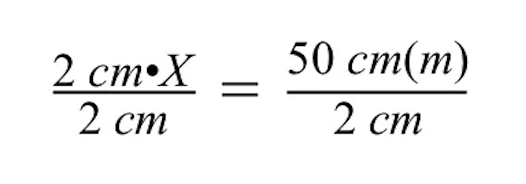
Her iki tarafı 2 cm'ye böldüğümüzde, cm birimleri eşittir işaretinin sol ve sağ taraflarında birbirini götürür ve sağ tarafta sadece metre (m) kalır.
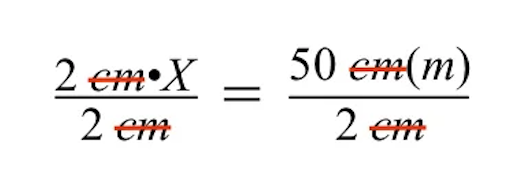
Daha da basitleştirdiğimizde, sol tarafın, gri binanın bilinmeyen gerçek boyutuna, yani X değişkenine indirgendiğini görüyoruz.
- Sağ tarafta 25 m. kaldı. Dolayısıyla gri binanın bilinmeyen gerçek boyutu 25 m'dir.
- Bu mantıklıdır, çünkü çizim boyutu için 2 cm, gerçek boyut için 50 metreye orantılıysa, bunu 1 cm için yarıya indirdiğimizde 25 metreye eşit olması gerekir.
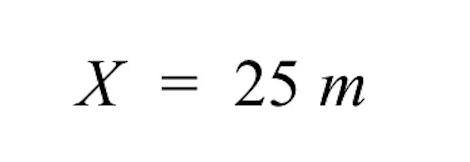
S:Çizime gerçekten 80 metre yüksekliğinde bir tuğla bina eklemek isteseydik ne olurdu? Kaç santimetre olmalı?
A:3.2 santimetre. Aşağıdaki açıklamayı inceleyin:
Oranlar iki oranın eşit olduğunu gösterir.
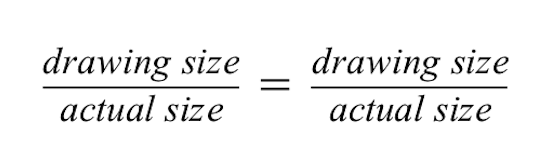
Soldaki oran için kırmızı binanın çiziminin 2 cm boyunda olduğunu ancak kırmızı binanın gerçek boyutunun 50 metre olduğunu biliyoruz.
- Çizim boyutunun payda, gerçek boyutun ise paydada olduğunu unutmayın. Her iki oranın da aynı kalması önemlidir, böylece eşit kalırlar.
- Gri binanın çizim boyutunun 1 cm olduğunu bildiğimizden bunu ikinci orandaki paya koyacağız.
- Paydaya gri binanın gerçek büyüklüğü girecek ancak bu büyüklüğü henüz bilmiyoruz, hesaplamamız gerekiyor. O halde şimdilik X değişkenini oraya koyacağız.
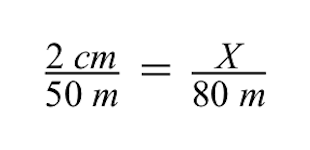
Tuğla binanın bilinmeyen çizim boyutu olan X değişkenini çözmek için çapraz çarpma yöntemini kullanabiliriz.
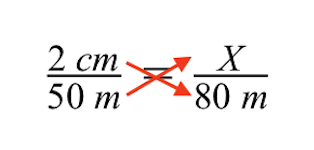
Çapraz çarpımı kullanarak aşağıdaki sonucu elde ederiz. Bir sonraki adım, X değişkeni ile gösterilen gri binanın bilinmeyen boyutunu çözmektir.
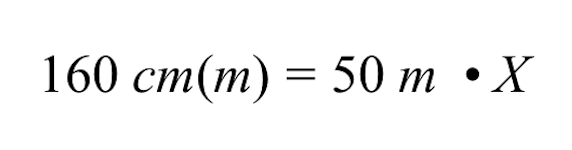
X değişkenini bulmak için, 50 m ile X'in çarpımını her iki tarafı da 50 m'ye bölerek geri almalıyız.
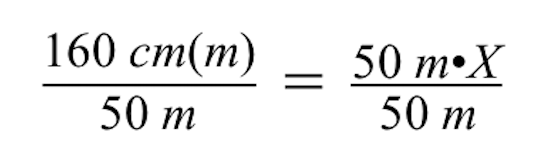
Her iki tarafı 50 m'ye böldüğümüzde, eşittir işaretinin sol ve sağ taraflarındaki m (metre) birimleri birbirini götürür ve sol tarafta sadece santimetre (cm) kalır.
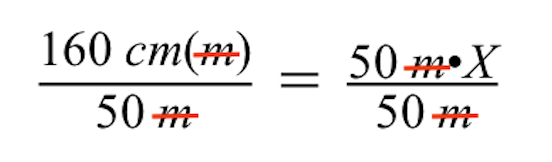
Daha da basitleştirdiğimizde, sağ tarafın, X değişkeniyle gösterilen, tuğla binanın bilinmeyen çizim boyutuna indirgendiğini görüyoruz.
- Sol tarafta 3.2 cm'lik bir boşluk kaldı. Dolayısıyla tuğla binanın bilinmeyen çizim boyutu 3,2 cm'dir.