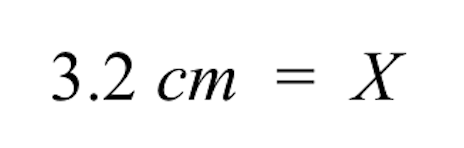पैमाने को समझना

इस पृष्ठ का उद्देश्य छात्रों को रेस कोर्स डिजाइनिंग और स्केलिंग तथा बाद में रोबो रैली चैलेंज में पूरा करने के लिए आवश्यक स्केलिंग के लिए अभ्यास और संदर्भ प्रदान करना है।

प्रेरित चर्चा प्रश्नों की समीक्षा के लिए विद्यार्थियों को पूरी कक्षा में चर्चा में शामिल करें। विद्यार्थियों से कहें कि वे अपना काम और विचार अपनी इंजीनियरिंग नोटबुक में लिखें।

कुछ छात्रों के लिए स्केलिंग एक कठिन अवधारणा हो सकती है। छात्रों को गणित से संबंधित अभ्यास कराने के बजाय, चर्चा कराएं ताकि छात्र अपने सहपाठियों को समझा सकें कि वे स्केलिंग के बारे में कैसे तर्क करते हैं।
प्रश्न:शहर के चित्र में एक लाल इमारत 2 सेंटीमीटर ऊंची है, लेकिन वास्तव में यह 50 मीटर ऊंची है। चित्र में इसके बगल में स्थित ग्रे रंग की इमारत केवल 1 सेंटीमीटर ऊंची है। वह अगली इमारत वास्तव में कितनी ऊँची है?
A:यह वास्तव में 25 मीटर ऊँची है। नीचे स्पष्टीकरण देखें:

अनुपात यह दर्शाता है कि दो अनुपात बराबर हैं।

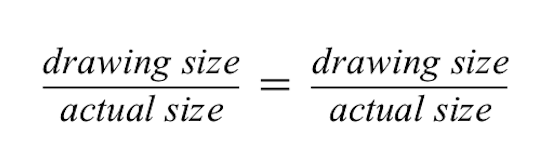
बाईं ओर के अनुपात के लिए, हम जानते हैं कि लाल इमारत का चित्र 2 सेमी लंबा है लेकिन लाल इमारत का वास्तविक आकार 50 मीटर है।

• ध्यान दें कि ड्राइंग का आकार अंश में है और वास्तविक आकार हर में है। दोनों अनुपातों के लिए इन्हें समान रखना महत्वपूर्ण है ताकि वे बराबर रहें।
• चूंकि हम जानते हैं कि ग्रे रंग की इमारत का ड्राइंग आकार 1 सेमी है, इसलिए हम इसे दूसरे अनुपात में अंश में रखेंगे।
• ग्रे बिल्डिंग का वास्तविक आकार हर में जाएगा, लेकिन हमें अभी तक यह आकार नहीं पता है, हमें गणना करने की आवश्यकता है। तो, अभी के लिए हम वहां चर X रखेंगे।

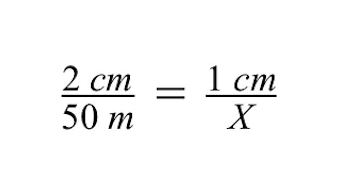
ग्रे बिल्डिंग के अज्ञात वास्तविक आकार, चर X को हल करने के लिए, हम क्रॉस गुणन की विधि का उपयोग कर सकते हैं।

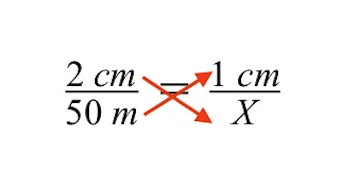
क्रॉस गुणन का उपयोग करने से हमें निम्नलिखित परिणाम प्राप्त होते हैं। अगला चरण चर X द्वारा निर्दिष्ट ग्रे बिल्डिंग के अज्ञात आकार को हल करना है।

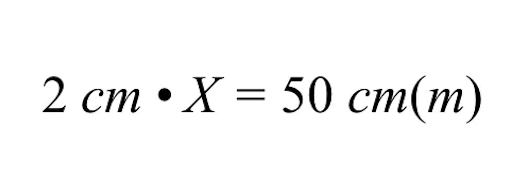
X को हल करने के लिए, हमें समीकरण के दोनों पक्षों को 2 सेमी से विभाजित करके चर X के 2 सेमी गुणा के गुणन को पूर्ववत करना होगा।

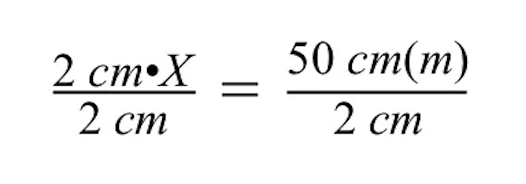
ध्यान दें कि जब दोनों पक्षों को 2 सेमी से विभाजित किया जाता है, तो सेमी की इकाइयाँ बराबर चिह्न के बाएँ और दाएँ पक्षों पर रद्द हो जाती हैं, तथा दाएँ पक्ष पर केवल मीटर (m) बचता है।

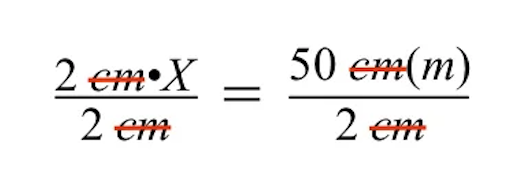
इसे और सरल करने पर, हम देखते हैं कि बाईं ओर केवल ग्रे बिल्डिंग का अज्ञात वास्तविक आकार रह जाता है, जिसे चर X द्वारा दर्शाया जाता है।

• दाहिनी ओर, हमारे पास 25 मीटर बचते हैं। इस प्रकार, ग्रे इमारत का अज्ञात वास्तविक आकार 25 मीटर है।
• यह उचित है, क्योंकि यदि चित्र के आकार के लिए 2 सेमी वास्तविक आकार के 50 मीटर के समानुपाती है, तो उसे आधा काटने पर 1 सेमी 25 मीटर के बराबर होगा।

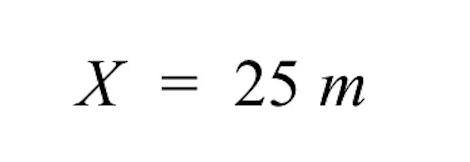
प्रश्न:यदि हम ड्राइंग में एक ईंट की इमारत जोड़ना चाहते हैं जो वास्तव में 80 मीटर ऊंची है तो क्या होगा? यह कितने सेंटीमीटर होना चाहिए?
A:3.2 सेंटीमीटर. नीचे स्पष्टीकरण देखें:

अनुपात यह दर्शाता है कि दोनों अनुपात बराबर हैं।

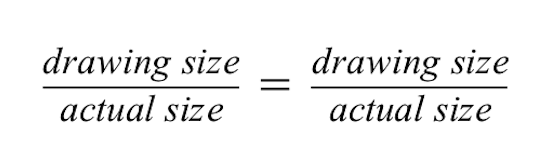
बाईं ओर के अनुपात के लिए, हम जानते हैं कि लाल इमारत का चित्र 2 सेमी लंबा है लेकिन लाल इमारत का वास्तविक आकार 50 मीटर है।

• ध्यान दें कि ड्राइंग का आकार अंश में है और वास्तविक आकार हर में है। दोनों अनुपातों के लिए इन्हें समान रखना महत्वपूर्ण है ताकि वे बराबर रहें।
• चूंकि हम जानते हैं कि ग्रे रंग की इमारत का ड्राइंग आकार 1 सेमी है, इसलिए हम इसे दूसरे अनुपात में अंश में रखेंगे।
• ग्रे बिल्डिंग का वास्तविक आकार हर में जाएगा, लेकिन हमें अभी तक यह आकार नहीं पता है, हमें गणना करने की आवश्यकता है। तो, अभी के लिए हम वहां चर X रखेंगे।

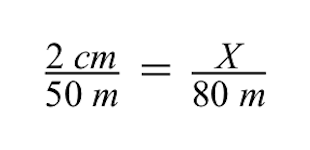
ईंट की इमारत के अज्ञात ड्राइंग आकार, चर X को हल करने के लिए, हम क्रॉस गुणन की विधि का उपयोग कर सकते हैं।

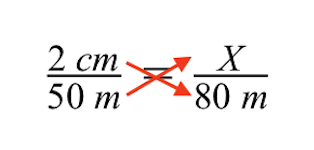
क्रॉस गुणन का उपयोग करने से हमें निम्नलिखित परिणाम प्राप्त होते हैं। अगला चरण चर X द्वारा निर्दिष्ट ग्रे बिल्डिंग के अज्ञात आकार को हल करना है।

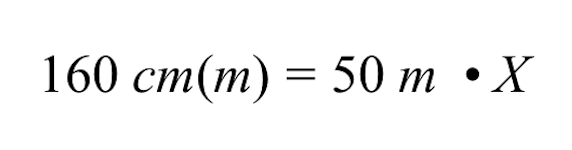
चर X को हल करने के लिए, हमें 50 m गुणा X के गुणनफल को दोनों पक्षों को 50 m से विभाजित करके पूर्ववत करना होगा।

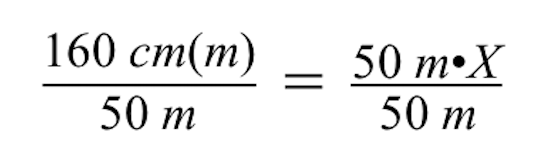
ध्यान दें कि जब दोनों पक्षों को 50 मीटर से विभाजित किया जाता है, तो मीटर की इकाइयाँ बराबर चिह्न के बाएँ और दाएँ पक्षों पर रद्द हो जाती हैं, तथा बाएँ पक्ष पर केवल सेंटीमीटर (सेमी) बचता है।

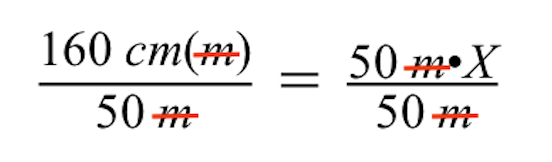
सरलीकरण को और आगे बढ़ाते हुए, हम देखते हैं कि दाईं ओर ईंट की इमारत का केवल हमारा अज्ञात आरेख आकार रह जाता है, जिसे चर X द्वारा दर्शाया जाता है।

• बायीं ओर, हमारे पास 3.2 सेमी बचता है। इस प्रकार, ईंट की इमारत का अज्ञात ड्राइंग आकार 3.2 सेमी है।