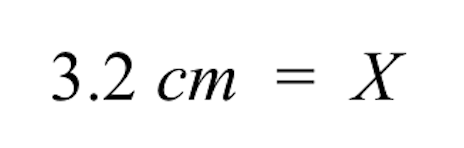Schaal begrijpen
![]() Toolbox voor leraren
-
Het doel van deze pagina
Toolbox voor leraren
-
Het doel van deze pagina
Het doel van deze pagina is om studenten te laten oefenen en context te bieden voor de schaling die ze moeten uitvoeren in het ontwerpen en schalen van een racebaan en later in de Robo Rally Challenge.
Betrek de leerlingen bij een discussie met de hele klas om de vragen uit het Motivatiegesprek te herhalen. Laat de leerlingen hun werk en gedachten in hun technisch notitieboekje schrijven.

Wat is "Schaal"?
Schaal is de relatie of verhouding tussen een ingestelde afstand op een kaart of tekening en de bijbehorende afstanden in het echte leven. Materialen die schaal gebruiken, zoals blauwdrukken, worden vaak als waardevoller beschouwd omdat ze de gebruiker in staat stellen om afstand visueel waar te nemen, waardoor ze effectievere modellen worden. Het kunnen converteren van metingen bij het werken met schaal is belangrijk voor carrières waarin kaarten, blauwdrukken en architecturale modellen zijn opgenomen. Professionals zoals architecten, ingenieurs, militairen en decorontwerpers maken allemaal op de een of andere manier gebruik van schaal in hun sector.
Het ontwikkelen van een gedetailleerde schets als plattegrond is een belangrijke stap in het technisch ontwerpproces. Wanneer we een geschaalde kopie van een object maken, moeten het origineel en de kopie dezelfde verhoudingen hebben. Om te laten zien in hoeverre een object daadwerkelijk is verkleind (of opgeschaald), maken we vaak gebruik van ratio's. Deze verhoudingen worden weergegeven op de geschaalde kopie, zodat het echte object correct kan worden weergegeven. Een schaal op een tekening kan bijvoorbeeld worden weergegeven als 1 cm = 20 m. Dit laat een team weten dat voor elke 1 cm op de schets de werkelijke meting 20 m is. Dus als een muur op de schets wordt weergegeven als 4 cm, moet de real-life muur 80 m zijn. Wanneer ingenieurs zaken als snelwegen of gebouwen aanleggen, worden de schaalplannen continu gecontroleerd om er zeker van te zijn dat de verhoudingen altijd correct zijn. Het opsplitsen van het real-life model in secties en controleren of de verhoudingen correct zijn tijdens het voltooien van elke sectie is een manier waarop teams werken om ervoor te zorgen dat ze op schaal blijven. Fouten kunnen leiden tot een verlies van aanzienlijke tijd, geld en materialen, dus het is essentieel om de nauwkeurigheid van de weegschaal in acht te nemen.
![]() Motiveer discussie
Motiveer discussie
Schalen kan voor sommige studenten een lastig concept zijn om toe te passen. In plaats van leerlingen de wiskunde te laten oefenen, kunt u een discussie voeren, zodat leerlingen aan klasgenoten kunnen uitleggen hoe ze redeneren over schaal.
Vraag:Een rood gebouw op een tekening van de stad is 2 centimeter hoog, maar het is in werkelijkheid 50 meter hoog. Het grijze gebouw ernaast op de tekening is slechts 1 centimeter hoog. Hoe hoog is het volgende gebouw werkelijk?
A:Het is werkelijk 25 meter hoog. Zie onderstaande uitleg:
Verhoudingen geven aan dat twee verhoudingen gelijk zijn.
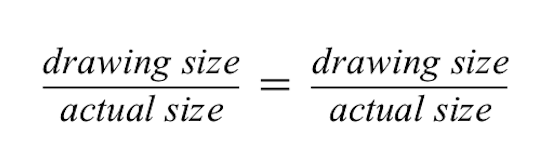
Voor de verhouding links geldt dat het getekende rode gebouw 2 cm hoog is, maar dat de werkelijke grootte van het rode gebouw 50 meter is.
- Let op: de tekeninggrootte staat in de teller en de werkelijke grootte in de noemer. Het is belangrijk om deze waarden voor beide verhoudingen gelijk te houden, zodat ze gelijk blijven.
- Omdat we weten dat de tekengrootte van het grijze gebouw 1 cm is, vullen we dit in de teller van de tweede verhouding in.
- De werkelijke grootte van het grijze gebouw komt in de noemer, maar deze grootte weten we nog niet, die moeten we berekenen. Dus voor nu zullen we de variabele X daar plaatsen.
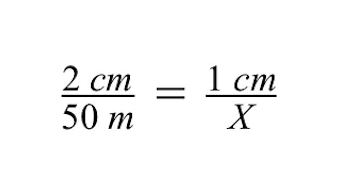
Om de variabele X (de onbekende werkelijke grootte van het grijze gebouw) op te lossen, kunnen we de methode van kruislingse vermenigvuldiging gebruiken.
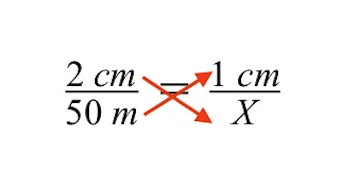
Door kruislings vermenigvuldigen krijgen we het volgende: De volgende stap is om de onbekende grootte van het grijze gebouw, aangegeven door de variabele X, op te lossen.
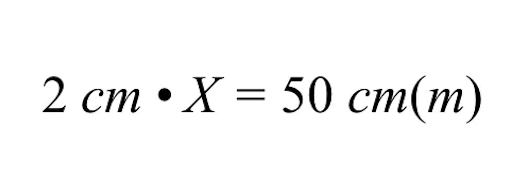
Om X op te lossen, moeten we de vermenigvuldiging van 2 cm met de variabele X ongedaan maken door beide zijden van de vergelijking te delen door 2 cm.
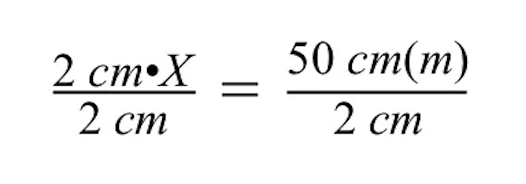
Let op: wanneer je beide zijden door 2 cm deelt, vallen de eenheden cm aan de linker- en rechterkant van het gelijkteken weg. Aan de rechterkant blijven alleen meters (m) over.
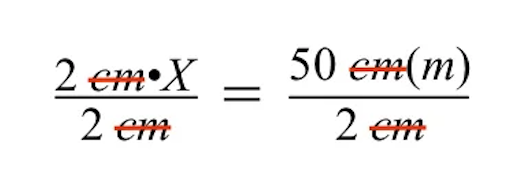
Als we het nog verder vereenvoudigen, zien we dat de linkerkant wordt teruggebracht tot alleen de onbekende werkelijke grootte van het grijze gebouw, weergegeven door de variabele X.
- Aan de rechterkant hebben we nog 25 m over. De onbekende werkelijke grootte van het grijze gebouw is dus 25 m.
- Dit is redelijk, want als 2 cm voor de getekende maat in verhouding staat tot 50 meter voor de werkelijke maat, dan zou het halveren van 1 cm gelijk moeten zijn aan 25 meter.
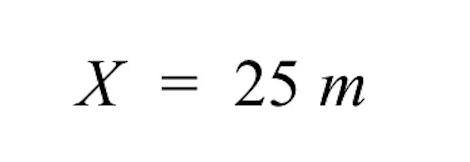
V:Wat als we een bakstenen gebouw dat echt 80 meter hoog is, aan de tekening wilden toevoegen? Hoeveel centimeter moet het zijn?
A:3,2 centimeter. Zie onderstaande uitleg:
Verhoudingen geven aan dat de twee verhoudingen gelijk zijn.
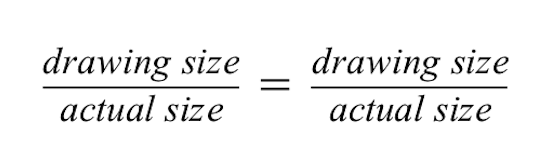
Voor de verhouding links geldt dat het getekende rode gebouw 2 cm hoog is, maar dat de werkelijke grootte van het rode gebouw 50 meter is.
- Let op: de tekeninggrootte staat in de teller en de werkelijke grootte staat in de noemer. Het is belangrijk om deze waarden voor beide verhoudingen gelijk te houden, zodat ze gelijk blijven.
- Omdat we weten dat de tekengrootte van het grijze gebouw 1 cm is, vullen we dit in de teller van de tweede verhouding in.
- De werkelijke grootte van het grijze gebouw komt in de noemer, maar deze grootte weten we nog niet, die moeten we berekenen. Dus voor nu zullen we de variabele X daar plaatsen.
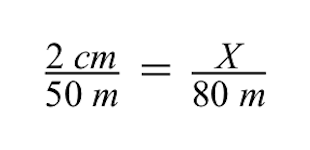
Om de variabele X, de onbekende tekeninggrootte van het bakstenen gebouw, op te lossen, kunnen we de methode van kruislingse vermenigvuldiging gebruiken.
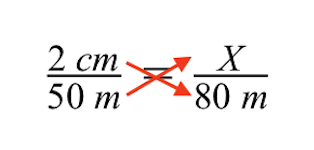
Door kruislings vermenigvuldigen krijgen we het volgende: De volgende stap is om de onbekende grootte van het grijze gebouw, aangegeven door de variabele X, op te lossen.
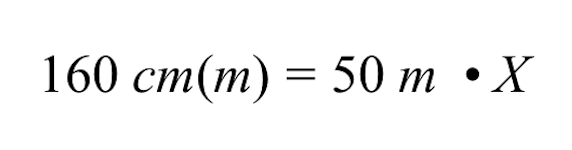
Om de variabele X te berekenen, moeten we de vermenigvuldiging van 50 m met X ongedaan maken door beide zijden te delen door 50 m.
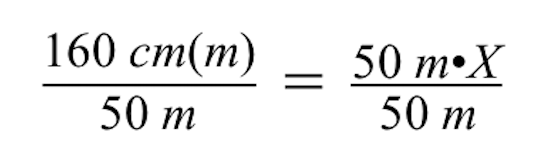
Let op: wanneer u beide zijden deelt door 50 m, dan worden de eenheden m (meter) aan de linker- en rechterkant van het gelijkteken opgeheven. Aan de linkerkant blijft alleen centimeter (cm) over.
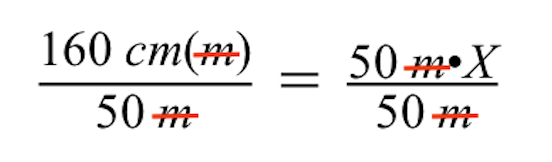
Als we het nog verder vereenvoudigen, zien we dat de rechterkant wordt teruggebracht tot alleen de onbekende grootte van onze tekening van het bakstenen gebouw, weergegeven door de variabele X.
- Aan de linkerkant houden we 3,2 cm over. De onbekende tekeninggrootte van het bakstenen gebouw is dus 3,2 cm.