পটভূমি
লোকেরা তাদের কাজগুলি সম্পন্ন করতে এবং সমস্যা সমাধানে সহায়তা করার জন্য প্রতিদিন সরঞ্জামগুলি ব্যবহার করে । এই সংখ্যার রেখা: সংযোজন ইউনিট আপনাকে এবং আপনার শিক্ষার্থীদের নির্দিষ্ট সরঞ্জামগুলির সাথে পরিচিত করবে যা সংযোজন সমীকরণগুলি সমাধান করতে সহায়তা করবে । আপনার শিক্ষার্থীরা যে সরঞ্জামগুলি ব্যবহার করবে তার মধ্যে একটি 123 রোবট, একটি সংখ্যা রেখা এবং ম্যানিপুলেটিভ রয়েছে । শিক্ষার্থীরা সমীকরণগুলি কার্যকরভাবে সমাধান করার জন্য কীভাবে তাদের 123 রোবটকে একটি সংখ্যা লাইনে সরানো যায় তাও শিখবে ।
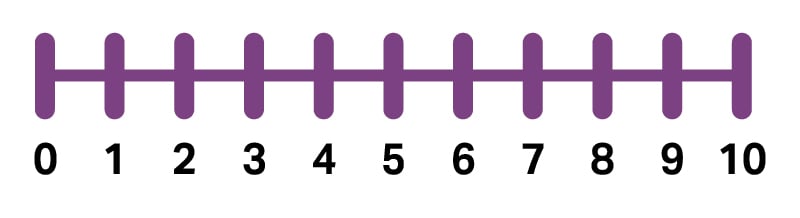
সংখ্যা রেখা
একটি সংখ্যা রেখা হল নির্দিষ্ট বিরতিতে চিহ্নিত সংখ্যার একটি রেখা বা একটি নির্দিষ্ট ক্রমে স্থাপিত সংখ্যা সহ সমান স্পেস । সংখ্যাগুলি শূন্য থেকে ধনাত্মকভাবে উপরে উঠতে থাকে এবং শূন্য থেকে নেতিবাচকভাবে নিচে নামতে থাকে । এটি সংখ্যা যোগ এবং বিয়োগ করার জন্য একটি দরকারী সরঞ্জাম । তদুপরি, সংখ্যা রেখা শিক্ষার্থীদের সমস্যা সমাধানের সময় সংখ্যাগুলি কল্পনা করতে সহায়তা করে । নম্বর লাইনটি এক-এক চিঠিপত্রের প্রতিনিধিত্ব করতেও সহায়তা করে । এক-এক চিঠিপত্র হল এক (সংশ্লিষ্ট ) নম্বর বা বস্তুর সাথে একটি বস্তুর মেলানোর ক্ষমতা । শিক্ষার্থীরা জানবে যে সংখ্যা রেখায় 123 রোবটের একটি চলন একটি সমীকরণে যোগ করা সংখ্যার সমান ।
গণনা কৌশল
শিক্ষার্থীরা যোগ এবং বিয়োগ শিখতে শুরু করার সময় বিভিন্ন গণনা কৌশল ব্যবহার করে । এই সত্যটি প্রথম গ্রেডের জন্য নিম্নলিখিত কমন কোর ম্যাথ স্ট্যান্ডার্ডে ধরা পড়েছে: যোগ এবং বিয়োগের সাথে সম্পর্কিত (যেমন, 2 যোগ করার জন্য 2 গণনা করে) । এই মানটি এই স্টেম ল্যাবের মূল ফোকাস । সমস্ত গণনা, গণনা এবং ফিরে গণনা সহ উভয় সংযোজন এবং বিয়োগের জন্য বিভিন্ন ধরণের গণনা কৌশল রয়েছে ।
যখন শিক্ষার্থীরা সমস্ত কৌশল গণনা করে (যোগ এবং বিয়োগের জন্য), তখন তারা 1 দিয়ে শুরু হয় এবং বস্তুর মোট সংখ্যা খুঁজে বের করতে গণনা করে । উদাহরণস্বরূপ, 7 + 2, শিক্ষার্থী 1 থেকে গণনা শুরু করবে, 7 পর্যন্ত গণনা করবে এবং 2 আরও গণনা করবে: 1, 2, 3, 4, 5, 6, 7...8, 9.
আরেকটি কৌশল যা শিক্ষার্থীরা ব্যবহার করতে পারে তা হল কৌশলের উপর গণনা (যোগ করার জন্য), শিক্ষার্থীরা 1 থেকে শুরু করার পরিবর্তে শুরু নম্বর থেকে গণনা করে । উদাহরণস্বরূপ, 7 + 2, শিক্ষার্থীরা 7...8, 9 থেকে শুরু করবে । যাইহোক, কৌশল (বিয়োগের জন্য) গণনা ব্যবহার করে, শিক্ষার্থীরা সাবট্রেন্ড নম্বর দিয়ে শুরু করে এবং মোট পৌঁছানোর জন্য গণনা করে । উদাহরণস্বরূপ, 12-5, শিক্ষার্থী 5 দিয়ে শুরু করবে এবং একের পর এক 12 পর্যন্ত গণনা করবে: 5...6, 7, 8, 9, 10, 11, 12 । উপরে উল্লিখিত
শেষ কৌশল, ফিরে গণনা করা, যখন শিক্ষার্থীরা বিয়োগ সমস্যার সমাধান করছে তখন ঘটে । কাউন্টিং ব্যাক কৌশল ব্যবহার করে শিক্ষার্থীরা মোট দিয়ে শুরু করবে এবং তারপরে বিয়োগ করা সংখ্যাটি আবার গণনা করবে । উদাহরণস্বরূপ, 12-5, শিক্ষার্থীরা 5 দিয়ে শুরু করবে এবং একের পর এক, 5...6, 7, 8, 9, 10, 11, 12 পর্যন্ত গণনা করবে ।
আপনি আপনার শিক্ষার্থীদের সাথে সমস্যা সমাধানের অনুশীলন করার সময়, দ্বিগুণ গণনার বিষয়ে শিক্ষার্থীদের সাথে একটি সাধারণ ভুল ধারণা সম্পর্কে সচেতন থাকুন । উদাহরণস্বরূপ, যদি কোনও শিক্ষার্থী 3 + 5 যোগ করে, তবে তারা 3 থেকে শুরু করে 7 এর উত্তর দিয়ে শেষ করতে পারে এবং 8 এর সঠিক উত্তর দিয়ে শেষ করতে পারে ।
শিক্ষার্থীদের জন্য সংযোজন এবং বিয়োগ সমীকরণগুলি গণনা করতে বা সমাধান করতে সহায়তা করার জন্য তাদের আঙ্গুলগুলি ব্যবহার করা খুব প্রচলিত । যেহেতু শিক্ষার্থীরা অন্যান্য গণনা কৌশলগুলি বোঝে এবং ব্যবহার করে, তাই সংযোজন এবং বিয়োগ সমীকরণগুলি সমাধান করার সময় শিক্ষার্থীদের তাদের আঙ্গুলগুলি ব্যবহার থেকে হালকাভাবে নিরুৎসাহিত করা উচিত । শিক্ষার্থীদের গণনা কৌশলগুলির বোঝার বিকাশ হিসাবে অনুশীলনকে সমর্থন করা এবং সরবরাহ করা তাদের ভবিষ্যতের শিক্ষায় আরও পরিশীলিত কৌশলগুলির সাথে সংযোগ স্থাপনের জন্য উত্সাহিত করা হয় ।
কারসাজি
ম্যানিপুলেটিভগুলি হ 'ল একটি ধারণার প্রতিনিধিত্ব করার জন্য হাতে-কলমে শেখার অভিজ্ঞতায় ব্যবহৃত শারীরিক বস্তু । এই ইউনিটে, ক্রেয়নগুলি প্রস্তাবিত ম্যানিপুলেটিভ । গণিতের সমীকরণগুলি সমাধান করার সময় শিক্ষার্থীদের জন্য ম্যানিপুলেটিভগুলি সহায়ক কারণ শিক্ষার্থীরা যে সংখ্যাগুলি তারা একসাথে যুক্ত করছে তা কল্পনা করতে পারে । ম্যানিপুলেটিভগুলি যোগ এবং বিয়োগের গণনা সম্পর্কিত শিক্ষার্থীদেরও সহায়তা করে । শিক্ষার্থীদের ক্রিয়াকলাপের সময় সংযোজন সমস্যার যোগফলের সমান সংখ্যার জন্য ম্যানিপুলেটিভগুলি গণনা করতে বলা হবে । ল্যাব 2 প্লে পার্ট 1 এবং প্লে পার্ট 2 এ শিক্ষার্থীরা যে সমীকরণটি পেতে পারে তার উত্তরের সাথে ম্যানিপুলেটিভগুলি মিলছে তা নিশ্চিত করার জন্য শিক্ষার্থীদের জন্য তাদের কাজ পরীক্ষা করার এটি একটি দুর্দান্ত উপায় ।
একের পর এক চিঠিপত্র
এটি সাধারণত একটি বস্তুকে একটি (সংশ্লিষ্ট) সংখ্যা বা বস্তুর সাথে মেলানোর ক্ষমতা হিসাবে ব্যাখ্যা করা হয় ।
-
উদাহরণ: 123 Robot = 1 মুভমেন্টে 1 বোতাম টিপুন

1টি বোতাম টিপুন 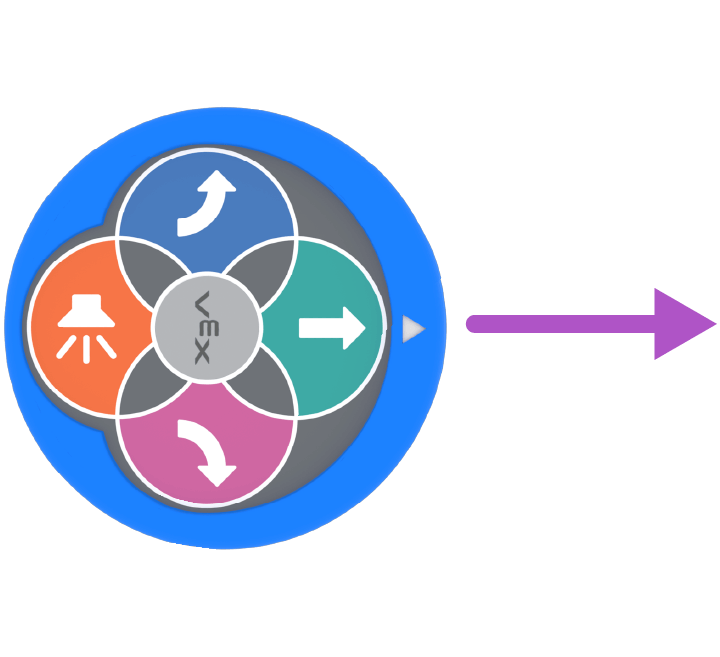
1 রোবট আন্দোলন
অ্যালগরিদম
অ্যালগরিদম হল একটি নির্দিষ্ট সমস্যা সমাধানের জন্য বা একটি কাজ সম্পাদনের জন্য তৈরি সু-সংজ্ঞায়িত নির্দেশাবলীর একটি তালিকা । অ্যালগরিদম সাধারণত কম্পিউটার বাস্তবায়নের নির্দেশাবলী উল্লেখ করে, তবে কীভাবে আপনার দাঁত ব্রাশ করবেন বা জেট স্কি পরিচালনা করার মতো আরও জটিল কাজগুলি অন্তর্ভুক্ত করতে পারে সে সম্পর্কে অন্যান্য নির্দেশাবলী অন্তর্ভুক্ত করতে পারে ।
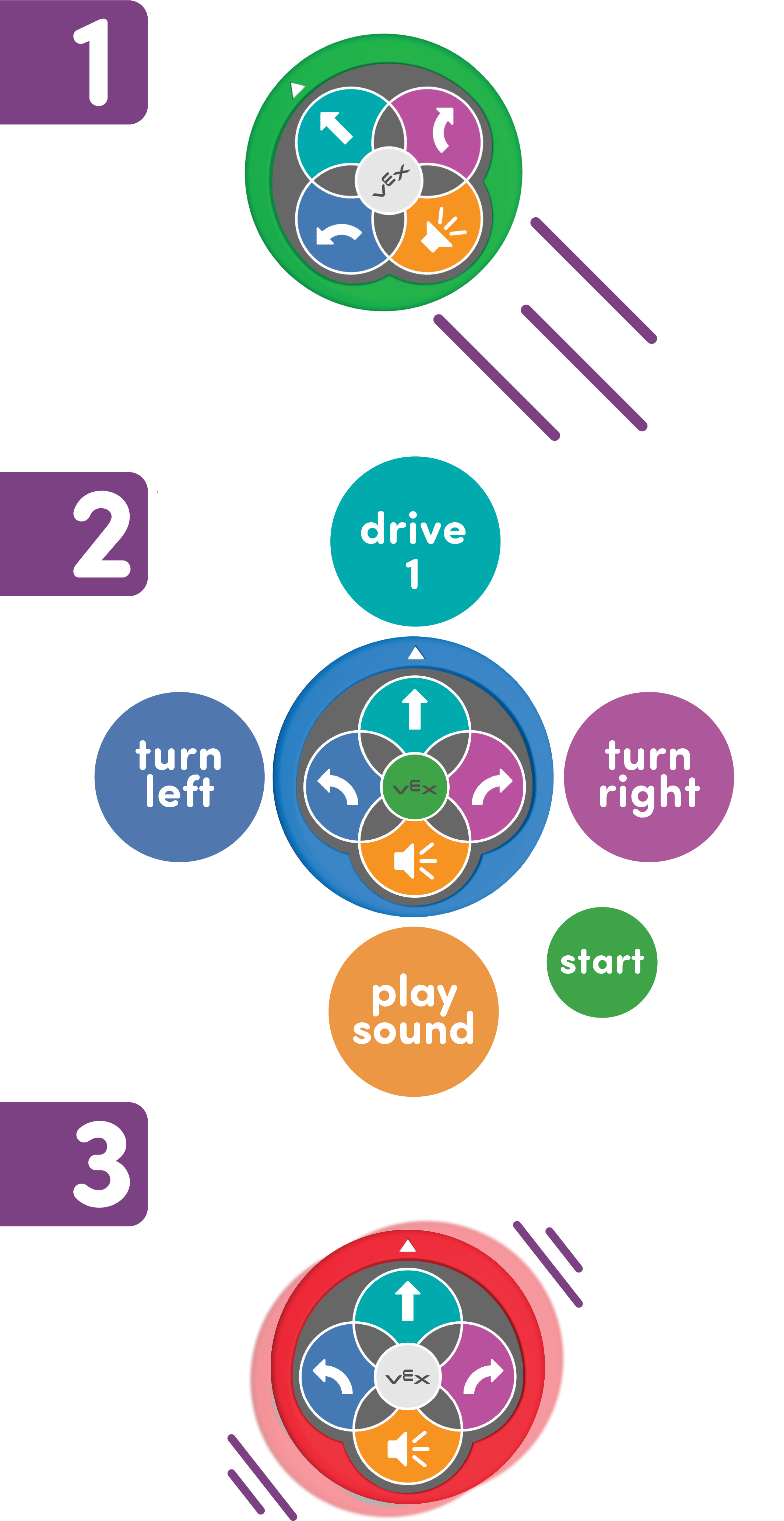
এই ইউনিটের সময়, শিক্ষার্থীরা 123 রোবট চালানোর জন্য একটি নির্দিষ্ট ক্রমে নির্দেশাবলীর একটি সেট অনুসরণ করবে । 123 Robot কীভাবে ব্যবহার করবেন সে সম্পর্কে আরও তথ্যের জন্য, VEX 123 Robot vex লাইব্রেরি নিবন্ধটি দেখুন। টাচ বোতাম ব্যবহার করে 123 রোবট কীভাবে কোড করবেন সে সম্পর্কে তথ্যের জন্য, 123 Robot vex লাইব্রেরি নিবন্ধে টাচ বোতামগুলির সাথে কোডিং দেখুন।
123 রোবট সরানোর অ্যালগরিদম হল:
- জেগে ওঠার জন্য চাপ দিন
- কোডে স্পর্শ করুন
- Shake to Erase