पृष्ठभूमि
लोग अपने कार्यों को पूरा करने और समस्याओं को सुलझाने के लिए प्रतिदिन उपकरणों का उपयोग करते हैं। यह संख्या रेखा: जोड़ इकाई आपको और आपके विद्यार्थियों को विशिष्ट उपकरणों से परिचित कराएगी जो जोड़ समीकरणों को हल करने में मदद करते हैं। आपके विद्यार्थी जिन उपकरणों का उपयोग करेंगे उनमें 123 रोबोट, संख्या रेखा और मैनिपुलेटिव्स शामिल हैं। छात्र यह भी सीखेंगे कि समीकरणों को हल करने के लिए अपने 123 रोबोट को संख्या रेखा पर प्रभावी ढंग से कैसे चलाना है।
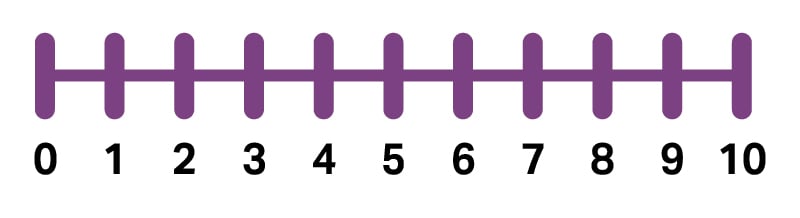
संख्या रेखा
संख्या रेखा संख्याओं की एक रेखा होती है जो निश्चित अंतरालों या समान स्थानों पर अंकित होती है तथा जिसमें संख्याएं एक विशेष क्रम में रखी जाती हैं। संख्याएं शून्य से धनात्मक रूप से ऊपर की ओर बढ़ती हैं तथा शून्य से ऋणात्मक रूप से नीचे की ओर बढ़ती हैं। यह संख्याओं को जोड़ने और घटाने के लिए एक उपयोगी उपकरण है। इसके अलावा, संख्या रेखा छात्रों को समस्याओं को हल करते समय संख्याओं की कल्पना करने में मदद करती है। संख्या रेखा एक-से-एक पत्राचार को दर्शाने में भी मदद करती है। एक-से-एक पत्राचार एक वस्तु को एक (संगत) संख्या या वस्तु की क्षमता है। विद्यार्थियों को पता चलेगा कि संख्या रेखा पर 123 रोबोट की एक चाल समीकरण में जोड़ी गई संख्या 1 के बराबर होती है।
गिनती की रणनीतियाँ
जोड़ और घटाव सीखना शुरू करते समय छात्र विभिन्न प्रकार की गिनती की रणनीतियों का उपयोग करते हैं। यह तथ्य प्रथम कक्षा के लिए निम्नलिखित कॉमन कोर गणित मानक में समाहित है: गिनती को जोड़ और घटाव से संबंधित करें (उदाहरण के लिए, 2 जोड़ने के लिए 2 पर गिनती करना)। यह मानक इस STEM लैब का मुख्य फोकस है। जोड़ और घटाव दोनों के लिए विभिन्न प्रकार की गिनती की रणनीतियाँ हैं, जिनमें सभी की गिनती, आगे की गिनती और पीछे की गिनती शामिल है।
जब छात्र सभी वस्तुओं की गिनती की रणनीति (जोड़ और घटाव के लिए) का उपयोग करते हैं, तो वे 1 से शुरू करते हैं और वस्तुओं की कुल संख्या ज्ञात करने के लिए गिनती करते हैं। उदाहरण के लिए, 7 + 2, छात्र 1 से गिनती शुरू करेगा, 7 तक गिनेगा, और 2 और गिनेगा: 1, 2, 3, 4, 5, 6, 7...8, 9।
एक अन्य रणनीति जिसका उपयोग छात्र कर सकते हैं वह है गिनती की रणनीति (जोड़ के लिए), छात्र 1 से शुरू करने के बजाय शुरुआती संख्या से गिनती करते हैं। उदाहरण के लिए, 7 + 2, छात्र 7...8, 9 से शुरू करेंगे। हालाँकि, गिनती की रणनीति (घटाव के लिए) का उपयोग करते हुए, छात्र घटाई गई संख्या से शुरू करते हैं और कुल तक पहुँचने के लिए गिनती करते हैं। उदाहरण के लिए, 12-5, छात्र 5 से शुरू करेगा और 12 तक इकाई से गिनती करेगा: 5...6, 7, 8, 9, 10, 11, 12.
ऊपर बताई गई अंतिम रणनीति, उल्टी गिनती, तब होती है जब छात्र घटाव की समस्याओं को हल कर रहे होते हैं। पीछे की ओर गिनती की रणनीति का उपयोग करने वाले छात्र कुल संख्या से शुरू करेंगे और फिर घटाई जाने वाली संख्या को पीछे की ओर गिनेंगे। उदाहरण के लिए, 12-5, छात्र 5 से शुरू करेंगे और 12 तक इकाई से गिनती करेंगे, 5...6, 7, 8, 9, 10, 11, 12।
जब आप अपने विद्यार्थियों के साथ समस्याओं को हल करने का अभ्यास करें, तो दोहरी गिनती के संबंध में विद्यार्थियों में व्याप्त एक आम गलत धारणा के प्रति सचेत रहें। उदाहरण के लिए, यदि कोई छात्र 3 + 5 जोड़ रहा है, तो वह 3 से शुरू करके 7 उत्तर पर समाप्त कर सकता है, बजाय इसके कि वह 3 से गिनते हुए 8 सही उत्तर पर समाप्त करे।
विद्यार्थियों द्वारा अपनी उंगलियों का उपयोग गिनती करने या जोड़-घटाव के समीकरणों को हल करने में करना बहुत प्रचलित है। जैसे-जैसे विद्यार्थी अन्य गणना रणनीतियों को समझते हैं और उनका उपयोग करते हैं, उन्हें जोड़ और घटाव के समीकरणों को हल करते समय अपनी उंगलियों का उपयोग करने से थोड़ा हतोत्साहित किया जाना चाहिए। विद्यार्थियों में गिनती की रणनीतियों की समझ विकसित करने के लिए उन्हें समर्थन देने और अभ्यास उपलब्ध कराने को प्रोत्साहित किया जाता है, ताकि भविष्य में सीखने के दौरान उन्हें अधिक परिष्कृत रणनीतियों से जोड़ा जा सके।
जोड़-तोड़
मैनिपुलेटिव्स भौतिक वस्तुएं हैं जिनका उपयोग किसी अवधारणा को प्रस्तुत करने के लिए व्यावहारिक शिक्षण अनुभवों में किया जाता है। इस इकाई में, क्रेयॉन को सहायक सामग्री के रूप में सुझाया गया है। गणित के समीकरणों को हल करते समय मैनिपुलेटिव्स विद्यार्थियों के लिए सहायक होते हैं, क्योंकि विद्यार्थी उन संख्याओं की कल्पना कर सकते हैं जिन्हें वे जोड़ रहे हैं। ये उपकरण विद्यार्थियों को गिनती को जोड़ और घटाव से जोड़ने में भी सहायता करते हैं। विद्यार्थियों को गतिविधियों के दौरान जोड़ समस्या के योग के बराबर संख्या के लिए जोड़-तोड़ की गणना करने के लिए कहा जाएगा। यह विद्यार्थियों के लिए अपने काम की जांच करने का एक शानदार तरीका है, जिससे यह सुनिश्चित किया जा सके कि मैनिपुलेटिव्स समीकरण के उत्तर से मेल खाते हैं, जो विद्यार्थियों को लैब 2 प्ले पार्ट 1 और प्ले पार्ट 2 में करने को मिलता है।
एक-से-एक पत्राचार
इसे आमतौर पर एक को (संगत) संख्या या वस्तु से की क्षमता के रूप में समझाया जाता है।
-
उदाहरण: 123 रोबोट पर 1 बटन दबाना = 1 गतिविधि

1 बटन दबाएँ 
1 रोबोट मूवमेंट
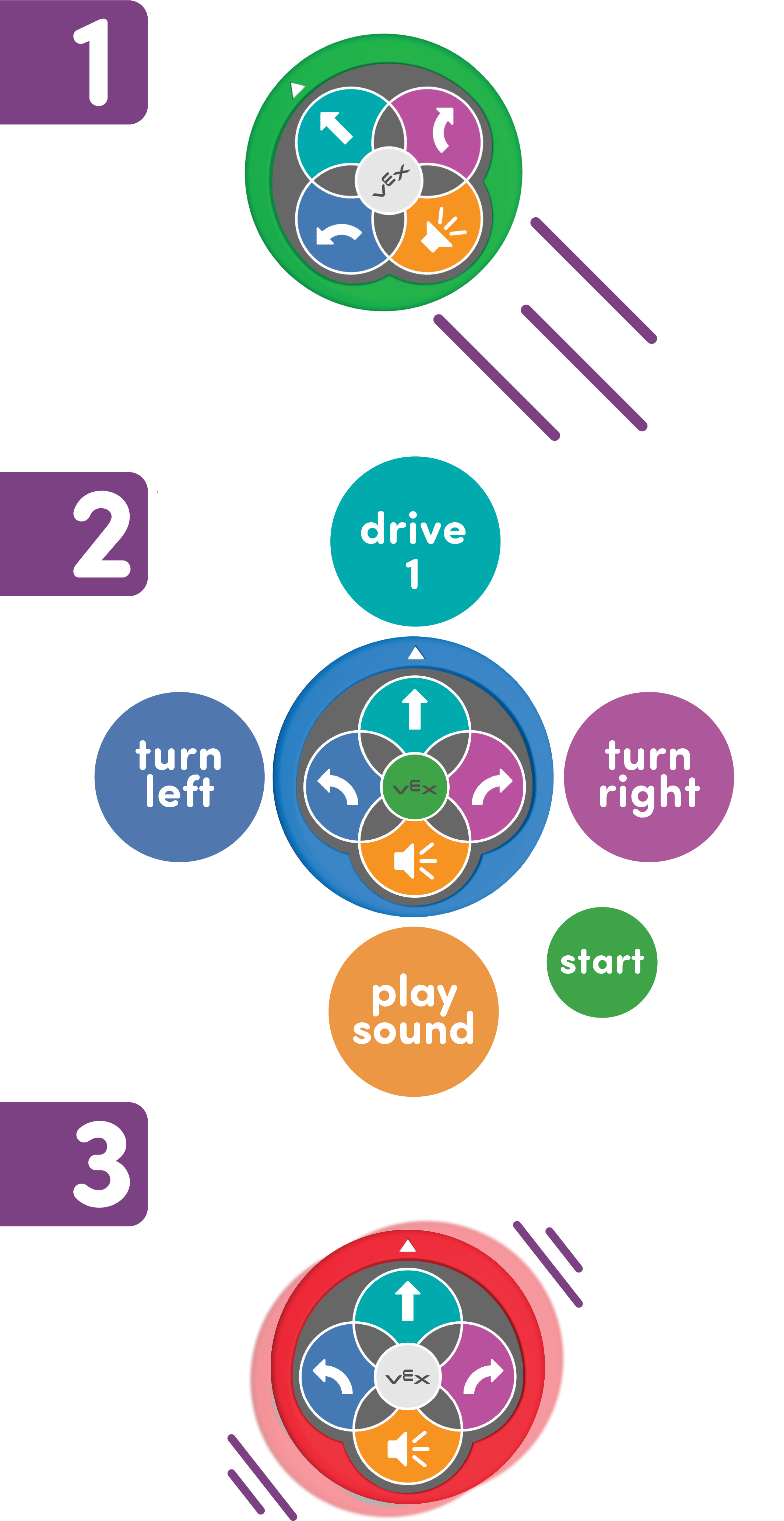
एल्गोरिथ्म
एल्गोरिदम एक विशिष्ट समस्या को हल करने या किसी कार्य को करने के लिए बनाए गए सुपरिभाषित निर्देशों की सूची है। एल्गोरिदम आमतौर पर कंप्यूटर द्वारा क्रियान्वित किये जाने योग्य निर्देशों का संदर्भ देते हैं, लेकिन इसमें दांतों को ब्रश करने के तरीके या जेट स्की चलाने जैसे अधिक जटिल कार्यों के बारे में अन्य निर्देश भी शामिल हो सकते हैं।
इस इकाई के दौरान, छात्र 123 रोबोट को संचालित करने के लिए एक विशिष्ट क्रम में निर्देशों के एक सेट का पालन करेंगे। 123 रोबोट का उपयोग करने के तरीके के बारे में अधिक जानकारी के लिए, VEX 123 रोबोट का उपयोग करना VEX लाइब्रेरी लेखदेखें। टच बटन का उपयोग करके 123 रोबोट को कोड करने के तरीके के बारे में जानकारी के लिए, 123 रोबोट VEX लाइब्रेरी लेखपर टच बटन के साथ देखें।
123 रोबोट को स्थानांतरित करने का एल्गोरिदम है:
- पुश टू वेक
- टच टू कोड
- मिटाने के लिए हिलाएँ