പശ്ചാത്തലം

ജോലികൾ പൂർത്തിയാക്കാനും പ്രശ്നങ്ങൾ പരിഹരിക്കാനും സഹായിക്കുന്നതിന് ആളുകൾ എല്ലാ ദിവസവും ഉപകരണങ്ങൾ ഉപയോഗിക്കുന്നു. ഈ സംഖ്യാരേഖ: സങ്കലന യൂണിറ്റ് സങ്കലന സമവാക്യങ്ങൾ പരിഹരിക്കാൻ സഹായിക്കുന്ന പ്രത്യേക ഉപകരണങ്ങൾ ഉപയോഗിച്ച് നിങ്ങൾക്കും നിങ്ങളുടെ വിദ്യാർത്ഥികൾക്കും പരിചയപ്പെടുത്തും. നിങ്ങളുടെ വിദ്യാർത്ഥികൾ ഉപയോഗിക്കുന്ന ഉപകരണങ്ങളിൽ ഒരു 123 റോബോട്ട്, ഒരു നമ്പർ ലൈൻ, കൃത്രിമത്വങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു. സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിന് 123 റോബോട്ടിനെ ഒരു നമ്പർ ലൈനിൽ എങ്ങനെ ഫലപ്രദമായി നീക്കാമെന്ന് വിദ്യാർത്ഥികൾ പഠിക്കും.

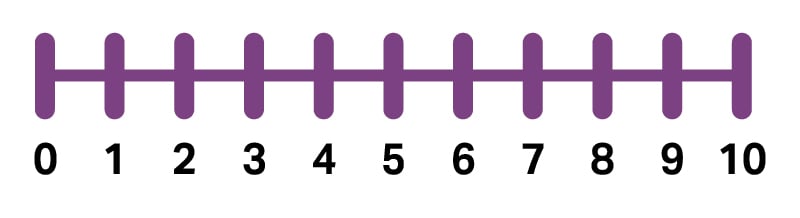
സംഖ്യാരേഖ

ഒരു സംഖ്യാരേഖ എന്നത് നിശ്ചിത ഇടവേളകളിലോ തുല്യ ഇടങ്ങളിലോ അടയാളപ്പെടുത്തിയിരിക്കുന്ന സംഖ്യകളുടെ ഒരു പ്രത്യേക ക്രമത്തിൽ അടുക്കിയിരിക്കുന്ന ഒരു വരിയാണ്. പൂജ്യത്തിൽ നിന്ന് പോസിറ്റീവ് ആയി സംഖ്യകൾ കയറുകയും പൂജ്യത്തിൽ നിന്ന് നെഗറ്റീവ് ആയി താഴുകയും ചെയ്യുന്നു. സംഖ്യകൾ കൂട്ടാനും കുറയ്ക്കാനും ഇത് ഉപയോഗപ്രദമായ ഒരു ഉപകരണമാണ്. മാത്രമല്ല, പ്രശ്നങ്ങൾ പരിഹരിക്കുമ്പോൾ സംഖ്യകളെ ദൃശ്യവൽക്കരിക്കാൻ സംഖ്യാരേഖ വിദ്യാർത്ഥികളെ സഹായിക്കുന്നു. സംഖ്യാരേഖ ഒരു വൺ-ടു-വൺ കത്തിടപാടിനെ പ്രതിനിധീകരിക്കാനും സഹായിക്കുന്നു. വൺ-ടു-വൺ കറസ്പോണ്ടൻസ് എന്നത് വൺ ഒബ്ജക്റ്റ് നെ ഒരു (അനുബന്ധ) സംഖ്യയോ വസ്തുവോ പൊരുത്തപ്പെടുത്താനുള്ള കഴിവാണ്. സംഖ്യാരേഖയിലെ 123 റോബോട്ടിന്റെ ഒരു ചലനം ഒരു സമവാക്യത്തിൽ ചേർക്കുന്ന സംഖ്യയ്ക്ക് തുല്യമാണെന്ന് വിദ്യാർത്ഥികൾക്ക് മനസ്സിലാകും.

കൃത്രിമത്വം

ഒരു ആശയത്തെ പ്രതിനിധീകരിക്കുന്നതിന് പ്രായോഗിക പഠനാനുഭവങ്ങളിൽ ഉപയോഗിക്കുന്ന ഭൗതിക വസ്തുക്കളാണ് കൃത്രിമത്വങ്ങൾ. ഈ യൂണിറ്റിൽ, ക്രയോണുകളാണ് നിർദ്ദേശിക്കപ്പെട്ട കൃത്രിമങ്ങൾ. ഗണിത സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ കൃത്രിമത്വങ്ങൾ വിദ്യാർത്ഥികൾക്ക് സഹായകരമാണ്, കാരണം വിദ്യാർത്ഥികൾക്ക് അവർ കൂട്ടുന്ന സംഖ്യകൾ ദൃശ്യവൽക്കരിക്കാൻ കഴിയും. എണ്ണലിനെ സങ്കലനവും കുറയ്ക്കലും ആയി ബന്ധപ്പെടുത്തുന്നതിൽ വിദ്യാർത്ഥികളെ സഹായിക്കുന്നതിനും ഈ കൃത്രിമത്വങ്ങൾ സഹായിക്കുന്നു. പ്രവർത്തനത്തിനിടയിൽ സങ്കലന പ്രശ്നത്തിന്റെ ആകെത്തുകയ്ക്ക് തുല്യമാകുന്നതിനായി കൃത്രിമത്വങ്ങൾ എണ്ണാൻ വിദ്യാർത്ഥികളോട് ആവശ്യപ്പെടും. ലാബ് 2 പ്ലേ പാർട്ട് 1, പ്ലേ പാർട്ട് 2 എന്നിവയിൽ വിദ്യാർത്ഥികൾക്ക് ചെയ്യാൻ കഴിയുന്ന സമവാക്യത്തിലേക്കുള്ള ഉത്തരവുമായി കൃത്രിമത്വങ്ങൾ പൊരുത്തപ്പെടുന്നുണ്ടെന്ന് ഉറപ്പാക്കാൻ വിദ്യാർത്ഥികൾക്ക് അവരുടെ ജോലി പരിശോധിക്കുന്നതിനുള്ള മികച്ച മാർഗമാണിത്.

വൺ-ടു-വൺ കറസ്‌പോണ്ടൻസ്

സാധാരണയായി ഇതിനെ ഒന്ന് വസ്തു ഒരു (അനുബന്ധ) സംഖ്യയുമായോ വസ്തുവുമായോ പൊരുത്തപ്പെടുത്താനുള്ള കഴിവായി വിശദീകരിക്കുന്നു.

• ഉദാഹരണം: 123 റോബോട്ടിൽ 1 ബട്ടൺ അമർത്തുക = 1 ചലനം.

  
  അമർത്തുക

  
  

അൽഗോരിതം

ഒരു പ്രത്യേക പ്രശ്നം പരിഹരിക്കുന്നതിനോ ഒരു ജോലി നിർവഹിക്കുന്നതിനോ വേണ്ടി തയ്യാറാക്കിയ, വ്യക്തമായി നിർവചിക്കപ്പെട്ട നിർദ്ദേശങ്ങളുടെ ഒരു പട്ടികയാണ് അൽഗോരിതങ്ങൾ. അൽഗോരിതങ്ങൾ സാധാരണയായി കമ്പ്യൂട്ടർ നടപ്പിലാക്കാവുന്ന നിർദ്ദേശങ്ങളെയാണ് പരാമർശിക്കുന്നത്, എന്നാൽ പല്ല് തേയ്ക്കുന്നതിനുള്ള മറ്റ് നിർദ്ദേശങ്ങളോ ജെറ്റ് സ്കീ പ്രവർത്തിപ്പിക്കുന്നത് പോലുള്ള സങ്കീർണ്ണമായ ജോലികളോ ഇതിൽ ഉൾപ്പെടുത്താം.

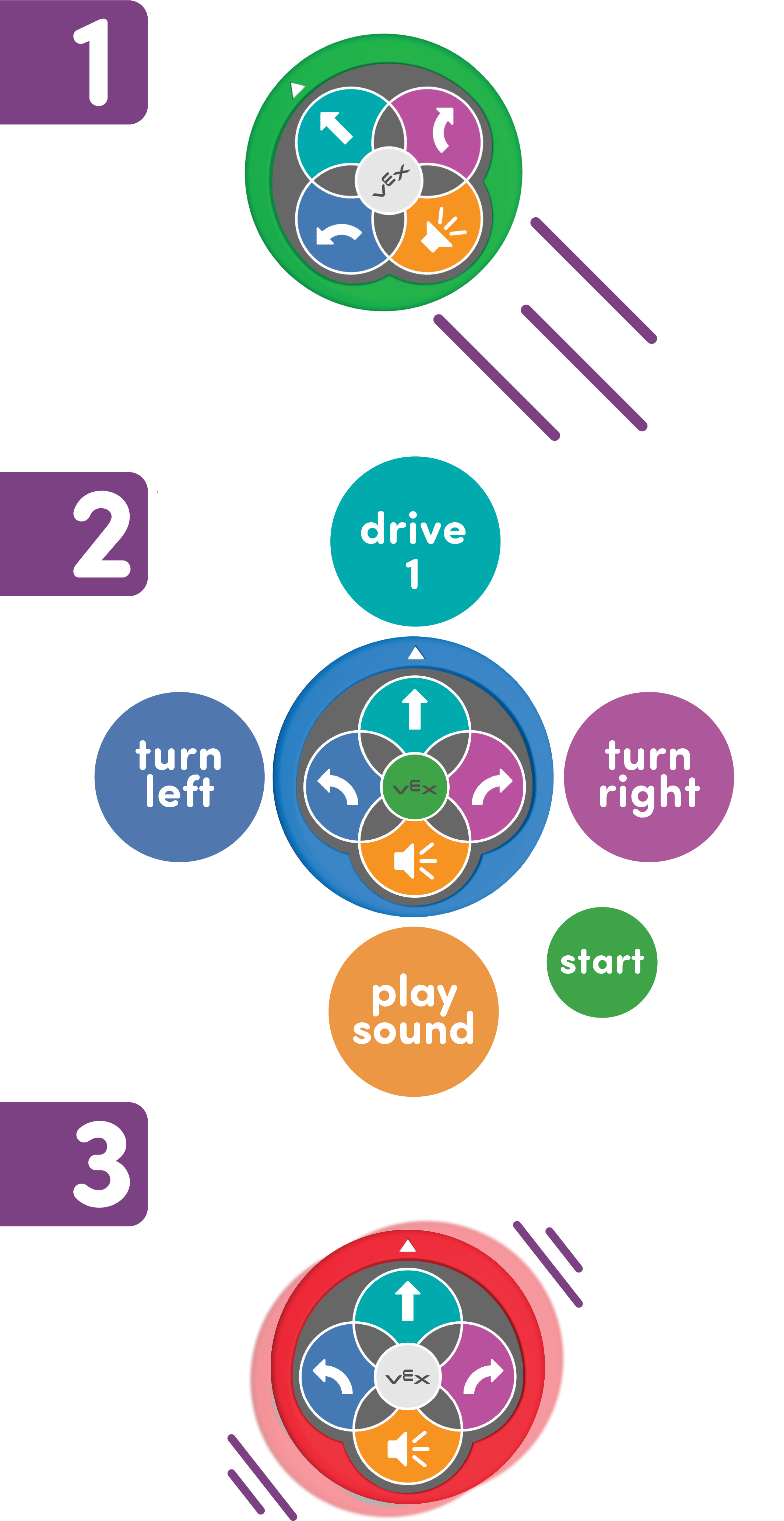
ഈ യൂണിറ്റിൽ, 123 റോബോട്ട് പ്രവർത്തിപ്പിക്കുന്നതിന് വിദ്യാർത്ഥികൾ ഒരു പ്രത്യേക ക്രമത്തിൽ ഒരു കൂട്ടം നിർദ്ദേശങ്ങൾ പാലിക്കും. 123 റോബോട്ട് എങ്ങനെ ഉപയോഗിക്കാം എന്നതിനെക്കുറിച്ചുള്ള കൂടുതൽ വിവരങ്ങൾക്ക്, VEX 123 റോബോട്ട് VEX ലൈബ്രറി ഉപയോഗിക്കൽ ലേഖനംകാണുക. ടച്ച് ബട്ടണുകൾ ഉപയോഗിച്ച് 123 റോബോട്ടിനെ എങ്ങനെ കോഡ് ചെയ്യാം എന്നതിനെക്കുറിച്ചുള്ള വിവരങ്ങൾക്ക്, 123 റോബോട്ട് VEX ലൈബ്രറി ലേഖനംടച്ച് ബട്ടണുകൾ ഉപയോഗിച്ചുള്ള കോഡിംഗ് കാണുക.

123 റോബോട്ട് നീക്കുന്നതിനുള്ള അൽഗോരിതം ഇതാണ്:

1. പുഷ് ടു വേക്ക്
2. കോഡ് ചെയ്യാൻ സ്പർശിക്കുക
3. മായ്ക്കാൻ കുലുക്കുക