Fundamentos DA invenção
As ferramentas são utilizadas todos os dias pelas pessoas para ajudá-las a realizar tarefas e resolver problemas. Esta Linha Numérica: Unidade de Adição irá familiarizar você e seus alunos com ferramentas específicas que ajudam a resolver equações de adição. As ferramentas que seus alunos usarão incluem um robô 123, uma linha numérica e manipuláveis. Os alunos também aprenderão a mover seu robô 123 em uma linha numérica de forma eficaz para resolver equações.
Linha numérica
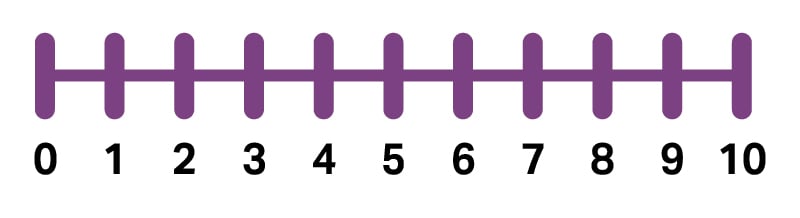
Uma linha numérica é uma linha de números marcados em determinados intervalos ou espaços iguais com números colocados em uma ordem específica. Os números sobem movendo-se positivamente de zero e descem movendo-se negativamente de zero. É uma ferramenta útil para somar e subtrair números. Além disso, a reta numérica ajuda os alunos a visualizar números enquanto resolvem problemas. A linha numérica também ajuda a representar uma correspondência um-para-um. A correspondência um-para-um é a capacidade de corresponder um objeto a um número ou objeto (correspondente). Os alunos saberão que um movimento do robô 123 na reta numérica é igual ao número um sendo adicionado a uma equação.
Estratégias de Contagem
Os alunos usam uma variedade de estratégias de contagem ao começar a aprender adição e subtração. Esse fato é capturado no seguinte Padrão Matemático Básico Comum para a primeira série: Relacione a Contagem à adição e subtração (por exemplo, contando com 2 para adicionar 2). Este padrão é o foco principal deste Laboratório STEM. Há uma variedade de estratégias de contagem para adição e subtração, incluindo contar tudo, contar com e contar de volta.
Quando os alunos usam a estratégia contar todos (para adição e subtração), eles começam com 1 e contam para encontrar o número total de objetos. Por exemplo, 7 + 2, o aluno começaria a contar de 1, contaria até 7 e contaria mais 2: 1, 2, 3, 4, 5, 6, 7...8, 9.
Outra estratégia que os alunos podem usar é a estratégia de contagem (para adição), os alunos contam a partir do número inicial em vez de começar em 1. Por exemplo, 7 + 2, os alunos começariam em 7...8, 9. No entanto, usando a estratégia de contagem em (para subtração), os alunos começam com o número de subtração e contam para alcançar o total. Por exemplo, 12-5, o aluno começaria com 5 e contaria até 12 por uns: 5...6, 7, 8, 9, 10, 11, 12.
A última estratégia mencionada acima, a contagem regressiva, acontece quando os alunos estão resolvendo problemas de subtração. Os alunos que usam a estratégia de contagem regressiva começarão com o total e, em seguida, contarão o número que está sendo subtraído. Por exemplo, 12-5, os alunos começarão com 5 e contarão até 12 por uns, 5...6, 7, 8, 9, 10, 11, 12.
Ao praticar a resolução de problemas com seus alunos, esteja ciente de um equívoco comum com os alunos em relação à contagem dupla. Por exemplo, se um aluno estiver adicionando 3 + 5, ele pode começar com 3 e terminar com uma resposta de 7, em vez de contar com 3 e terminar com a resposta correta de 8.
É muito comum que os alunos usem os dedos para contar ou ajudar a resolver equações de adição e subtração. À medida que os alunos entendem e usam outras estratégias de contagem, os alunos devem ser levemente desencorajados de usar os dedos ao resolver equações de adição e subtração. Apoiar e fornecer prática à medida que os alunos desenvolvem uma compreensão das estratégias de contagem é incentivado a fazer conexões com estratégias mais sofisticadas em sua aprendizagem futura.
Manipulativos
Os manipuladores são objetos físicos usados em experiências práticas de aprendizagem para representar um conceito. Nesta unidade, os lápis de cera são os manipuladores sugeridos. Os manipuladores são úteis para os alunos ao resolver equações matemáticas, porque os alunos podem visualizar os números que estão somando. Os manipuladores também ajudam os alunos a relacionar a contagem com a adição e a subtração. Os alunos serão solicitados a contar os manipuladores para igualar o mesmo número que a soma do problema de adição durante as atividades. Esta é uma ótima maneira de os alunos verificarem seu trabalho para garantir que os manipuladores correspondam à resposta à equação que os alunos conseguem fazer no Laboratório 2 Reproduzir a Parte 1 e Reproduzir a Parte 2.
Correspondência individual
Geralmente é explicado como a capacidade de corresponder um objeto a um número ou objeto (correspondente).
-
Exemplo: 1 botão pressionar no Robô 123 = 1 movimento

1 pressionar botão 
1 movimento do robô
Algoritmo
Algoritmos são uma lista de instruções bem definidas feitas para resolver um problema específico ou executar uma tarefa. Os algoritmos normalmente fazem referência a instruções implementáveis por computador, mas podem incluir outras instruções sobre como escovar os dentes ou tarefas mais complexas, como operar um jet ski.
Durante esta Unidade, os alunos seguirão um conjunto de instruções em uma ordem específica para operar o Robô 123. Para obter mais informações sobre como usar o Robô 123, consulte o artigo Using the VEX 123 Robot VEX Library. Para obter informações sobre como codificar o robô 123 usando os botões de toque, consulte o artigo Codificação com os botões de toque no 123 Robot VEX Library.
O algoritmo para mover o robô 123 é:
- Empurre para acordar
- Toque no código
- Agitar para Apagar