Background
Visualization is a strategy used to help students understand mathematical concepts. In this Unit, students will construct the Fractions build to help them visualize fractions and see the connections between whole equivalents and fractional equivalents. They will use VEX GO pieces to create visual representations of fractions, as well as practice writing and drawing them correctly.
What is a Fraction?
A fraction is a numerical representation of parts of a whole. The numerator tells you the number pieces in the fraction, and the denominator indicates the number of pieces in the whole. We see and use fractions to help us figure things out in our daily lives, from the number of pizzas to order to how much gasoline is left in a car’s gas tank. Understanding how fractions function and relate to whole numbers will be a skill that students will build upon as they learn more complex mathematics.

Why Visualize Fractions?
The concept of breaking a number into parts can be too abstract for some students to grasp. Creating visual representations of fractions helps them become more tangible, and enables students to see the connections between parts and whole more clearly. This can be done in a number of ways, from folding paper, to stacking proportional manipulatives or unit blocks, to drawing and coloring. Each enables the student to simultaneously see the parts and whole being represented by the fraction. It is easier to make sense of 2/4 = ½ when it is clearly visible that they are the same size.

Fractions Are Numbers Too
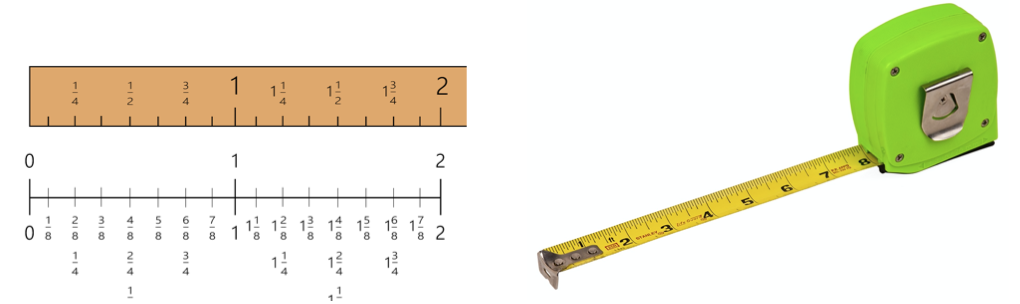
A fraction is a part of a number, and as such has a numerical value and sequence, just as whole numbers do. We see sequences of fractions every time we use a tape measure or look at the speedometer of a car. Sometimes students disconnect fractional values from whole number counting. In doing so, students struggle when asked to perform operations, like addition or multiplication, with fractions. Fractions can also be visualized in a sequential way. Students can use manipulatives like rulers, or make their own fractional number lines, to help understand the function of fractions in math, and real life applications.
Common Misconceptions About Fractions

As students begin to build understandings about fractions, there are certain misconceptions that frequently arise. It is important to dispel the misconceptions early on, so that they do not cause more confusion as work gets more complex.
Misconception: “The numerator has to be smaller than the denominator.”
It is easy to see how students might fall into this trap, as the first fractions they often encounter do follow this logic. Seeing fractions sequentially can help students visualize this as a fallacy. Teaching students that they can count in fractions, just as they can in whole numbers, is helpful. Writing whole numbers as fractions (3/1, 6/1, 9/1, etc.) can help make this clear, as well as questions like “What comes after 4/4?” (5/4, 6/4, 7/4, etc.)
Misconception: “The denominator gets smaller as the pieces get smaller.”
Again, this may seem logical to some degree, even though its opposite is actually true - as the denominator gets smaller, the pieces get larger (or as the denominator gets larger, the pieces get smaller.) Visualization of fractions can easily dispel this misconception for students, as they are able to see and feel the sizes of the pieces in connection to the fractions they represent. Using VEX GO Kit pieces can help make this visible for students individually, or as a group, and will be reinforced throughout the course of this Unit.
VEX GO Pieces
Blue and Yellow Connectors Serve a Specific Function
The various connectors can be used in many different ways, and in this build, the ability to build a wall on the outside of a structure is particularly important. As such, instead of the pins and beam construction you might think would construct the walls of a box, the blue and yellow connectors are used to create the sides. The blue and yellow connectors enable a right angle to be made that lies beside the bottom of the box, rather than inside of it, so that the space inside the box is a precise size to fit the plates and beams that will go inside. Both sides of the box are constructed in the same way, so that each base box is equal in size, and can be used to evaluate equivalent fractions inside it.

Proportional Plates and Beams Fit Together
The plates and beams of the VEX GO Kit are all proportionally related to one another in size and shape, and as such, fit together in precise ways (similar to Unit Blocks). This makes them ideal manipulatives for exploring the relationships between fractions in a tangible way. In addition to the activities with the Fractions build in the Lab, the beams and plates can be arranged and rearranged independently of the build to help make this visible to students, which is a helpful strategy for those students who may be struggling with making the connections.
