Hintergrund
Visualisierung ist eine Strategie, die Schülern das Verständnis mathematischer Konzepte erleichtern soll. In dieser Einheit werden die Schüler das Bruchsystem konstruieren, um ihnen zu helfen, Brüche zu visualisieren und die Verbindungen zwischen ganzen Äquivalenten und Bruchäquivalenten zu erkennen. Sie verwenden VEX GO-Teile, um visuelle Darstellungen von Brüchen zu erstellen und üben das richtige Schreiben und Zeichnen.
Was ist ein Bruch?
Ein Bruch ist eine numerische Darstellung von Teilen eines Ganzen. Der Zähler gibt die Anzahl der Teile des Bruchs an, und der Nenner gibt die Anzahl der Teile des Ganzen an. Wir sehen und verwenden Brüche, um Dinge in unserem täglichen Leben herauszufinden, von der Anzahl der zu bestellenden Pizzen bis hin zur verbleibenden Benzinmenge im Tank eines Autos. Das Verständnis der Funktionsweise von Brüchen und ihrer Beziehung zu ganzen Zahlen ist eine Fähigkeit, die die Schüler beim Erlernen komplexerer Mathematik weiterentwickeln werden.

Warum Brüche visualisieren?
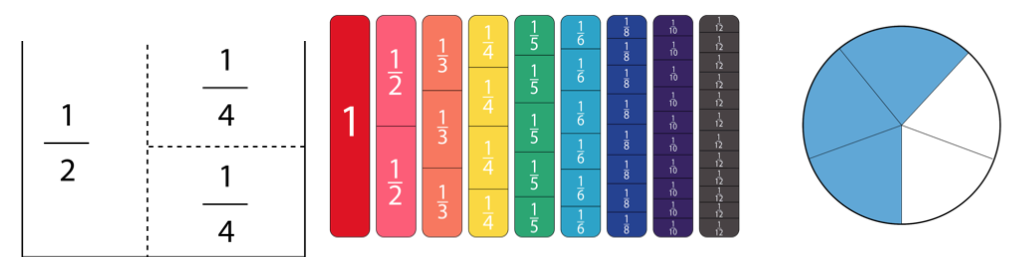
Das Konzept, eine Zahl in Teile zu zerlegen, kann für manche Schüler zu abstrakt sein. Durch die visuelle Darstellung von Brüchen werden diese greifbarer und Schüler können die Zusammenhänge zwischen Teilen und Ganzem klarer erkennen. Dies kann auf verschiedene Weise erfolgen, vom Papierfalten über das Stapeln proportionaler Manipulatoren oder Einheitsblöcke bis hin zum Zeichnen und Ausmalen. Jedes ermöglicht es dem Schüler, gleichzeitig die Teile und das Ganze zu sehen, die durch den Bruch dargestellt werden. Es ist einfacher, die Gleichung 2/4 = ½ zu verstehen, wenn klar erkennbar ist, dass es sich um die gleiche Größe handelt.
Auch Brüche sind Zahlen
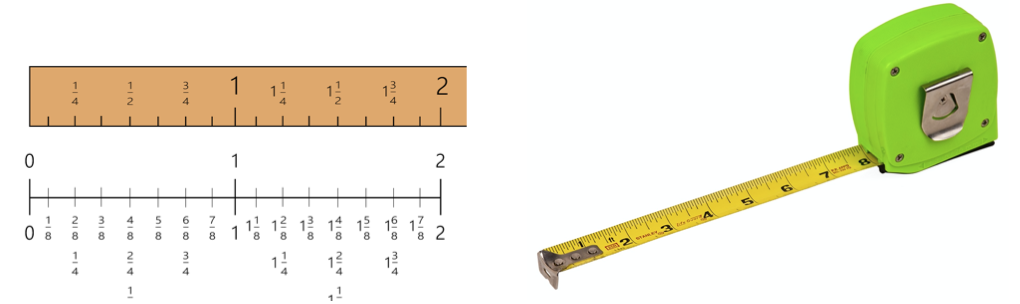
Ein Bruch ist ein Teil einer Zahl und hat als solcher, genau wie ganze Zahlen, einen numerischen Wert und eine Folge. Wir sehen Folgen von Brüchen jedes Mal, wenn wir ein Maßband verwenden oder auf den Tachometer eines Autos schauen. Manchmal trennen Schüler das Zählen von Bruchwerten vom Zählen von ganzen Zahlen. Daher haben die Schüler Schwierigkeiten, wenn sie aufgefordert werden, Rechenoperationen wie Addition oder Multiplikation mit Brüchen durchzuführen. Brüche können auch sequentiell visualisiert werden. Schüler können Hilfsmittel wie Lineale verwenden oder eigene Zahlenstrahlen für Brüche erstellen, um die Funktion von Brüchen in der Mathematik und in Anwendungen im wirklichen Leben besser zu verstehen.
Häufige Missverständnisse über Brüche

Wenn Schüler beginnen, ein Verständnis für Brüche zu entwickeln, treten häufig bestimmte Missverständnisse auf. Es ist wichtig, Missverständnisse frühzeitig auszuräumen, damit sie bei zunehmender Komplexität der Arbeit nicht zu noch größerer Verwirrung führen.
Missverständnis: „Der Zähler muss kleiner sein als der Nenner.“
Es ist leicht zu erkennen, wie Schüler in diese Falle tappen können, da die ersten Brüche, mit denen sie oft konfrontiert werden, dieser Logik folgen. Wenn Schüler Brüche in der Reihenfolge ihrer Entstehung sehen, kann ihnen das dabei helfen, sich vorzustellen, dass es sich um einen Trugschluss handelt. Es ist hilfreich, den Schülern beizubringen, dass sie in Brüchen genauso zählen können wie in ganzen Zahlen. Das Schreiben ganzer Zahlen als Brüche (3/1, 6/1, 9/1 usw.) kann dabei helfen, dies zu verdeutlichen, ebenso wie Fragen wie „Was kommt nach 4/4?“ (5/4, 6/4, 7/4 usw.)
Missverständnis: „Der Nenner wird kleiner, wenn die Teile kleiner werden.“
Auch dies mag bis zu einem gewissen Grad logisch erscheinen, obwohl das Gegenteil der Fall ist – wenn der Nenner kleiner wird, werden die Teile größer (oder wenn der Nenner größer wird, werden die Teile kleiner). Durch die Visualisierung von Brüchen kann dieser Irrtum bei Schülern leicht ausgeräumt werden, da sie die Größen der Teile im Zusammenhang mit den Brüchen, die sie darstellen, sehen und fühlen können. Die Verwendung von Teilen des VEX GO Kits kann dabei helfen, dies für die Schüler einzeln oder als Gruppe sichtbar zu machen, und wird im Verlauf dieser Einheit verstärkt.
VEX GO-Teile
Blaue und gelbe Anschlüsse erfüllen eine bestimmte Funktion
Die verschiedenen Verbindungselemente sind vielseitig einsetzbar und bei dieser Konstruktion ist insbesondere die Möglichkeit, eine Wand an der Außenseite eines Bauwerks zu errichten, von großer Bedeutung. Anstatt der Konstruktion aus Stiften und Balken, die man zum Bau der Wände einer Kiste erwarten würde, werden zum Erstellen der Seiten die blauen und gelben Verbindungsstücke verwendet. Die blauen und gelben Verbindungsstücke ermöglichen die Bildung eines rechten Winkels, der neben dem Boden der Box liegt und nicht darin, sodass der Raum innerhalb der Box genau die richtige Größe für die hineinpassenden Platten und Balken hat. Beide Seiten der Box sind gleich aufgebaut, so dass die Basisboxen jeweils die gleiche Größe aufweisen und zum Auswerten der darin enthaltenen äquivalenten Brüche verwendet werden können.

Proportionale Platten und Balken passen zusammen
Die Platten und Balken des VEX GO Kits sind alle in Größe und Form proportional zueinander und passen daher präzise zusammen (ähnlich wie Einheitsblöcke). Dies macht sie zu idealen Hilfsmitteln, um die Beziehungen zwischen Brüchen auf greifbare Weise zu erkunden. Zusätzlich zu den Aktivitäten mit dem Bruchrechnungsmodell im Labor können die Balken und Platten unabhängig vom Modell angeordnet und neu angeordnet werden, um dies den Schülern deutlich zu machen. Dies ist eine hilfreiche Strategie für Schüler, die möglicherweise Schwierigkeiten haben, die Zusammenhänge herzustellen.
