Fundo

A visualização é uma estratégia utilizada para ajudar os alunos a compreender conceitos matemáticos. Nesta unidade, os alunos vão construir a construção Frações para os ajudar a visualizar frações e a ver as ligações entre equivalentes inteiros e equivalentes fraccionários. Utilizarão peças VEX GO para criar representações visuais de frações, bem como praticarão a sua escrita e desenho corretamente.

O que é uma fração?

Uma fração é uma representação numérica de partes de um todo. O numerador indica o número de peças da fração e o denominador indica o número de peças do todo. Vemos e usamos frações para nos ajudar a descobrir coisas no nosso dia a dia, desde o número de pizzas encomendadas até à quantidade de gasolina que resta no depósito de um carro. Compreender como as frações funcionam e se relacionam com os números inteiros será uma competência que os alunos desenvolverão à medida que aprendem matemática mais complexa.

Porquê visualizar frações?

O conceito de dividir um número em partes pode ser demasiado abstrato para alguns alunos compreenderem. A criação de representações visuais de frações ajuda-as a tornarem-se mais tangíveis e permite aos alunos ver as ligações entre as partes e o todo com mais clareza. Isto pode ser feito de várias formas, desde dobrar papel, empilhar manipuladores proporcionais ou blocos unitários, até desenhar e colorir. Cada um permite ao aluno ver simultaneamente as partes e o todo sendo representados pela fração. É mais fácil compreender 2/4 = ½ quando é claramente visível que são do mesmo tamanho.

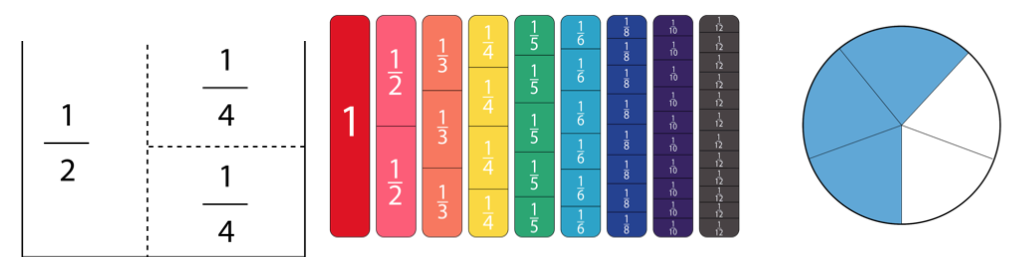
As frações também são números

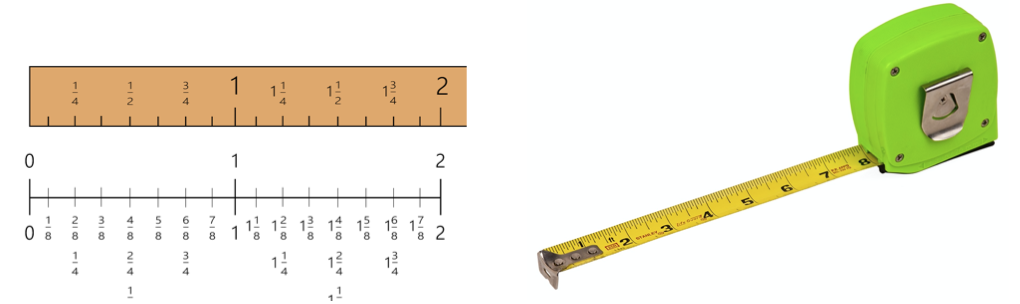
Uma fração faz parte de um número e, como tal, tem um valor numérico e uma sequência, tal como os números inteiros. Vemos sequências de frações sempre que utilizamos uma fita métrica ou olhamos para o velocímetro de um automóvel. Por vezes, os alunos desligam os valores fraccionários da contagem de números inteiros. Ao fazê-lo, os alunos têm dificuldade quando lhes é pedido para realizar operações, como a adição ou a multiplicação, com frações. As frações podem também ser visualizadas de forma sequencial. Os alunos podem utilizar instrumentos manipuláveis, como réguas, ou criar as suas próprias retas numéricas fracionadas, para ajudar a compreender a função das frações em matemática e em aplicações da vida real.

Equívocos comuns sobre as frações

À medida que os alunos começam a compreender as frações, surgem frequentemente certos equívocos. É importante dissipar os equívocos desde o início, para que não causem mais confusão à medida que o trabalho se torna mais complexo.

Equívoco: “O numerador tem de ser menor que o denominador.”
É fácil perceber como os alunos podem cair nesta armadilha, uma vez que as primeiras frações que encontram seguem frequentemente esta lógica. Ver as frações sequencialmente pode ajudar os alunos a visualizar isto como uma falácia. É útil ensinar aos alunos que conseguem contar em frações, tal como em números inteiros. Escrever números inteiros como frações (3/1, 6/1, 9/1, etc.) pode ajudar a tornar isto claro, assim como perguntas como “O que vem depois de 4/4?” (5/4, 6/4, 7/4, etc.)

Equívoco: “O denominador torna-se mais pequeno à medida que as peças se tornam mais pequenas.”
Mais uma vez, isto pode parecer lógico até certo ponto, embora o seu oposto seja realmente verdadeiro - à medida que o denominador fica mais pequeno, as peças ficam maiores (ou à medida que o denominador fica maior, as peças ficam mais pequenas). A visualização de frações pode facilmente dissipar este equívoco dos alunos, pois estes são capazes de ver e sentir os tamanhos das peças em relação às frações que representam. A utilização de peças do Kit VEX GO pode ajudar a tornar isso visível para os alunos individualmente ou em grupo, e será reforçado ao longo desta Unidade.

Peças VEX GO

Os conectores azuis e amarelos desempenham uma função específica

Os vários conectores podem ser utilizados de muitas formas diferentes e, nesta construção, a capacidade de construir uma parede no exterior de uma estrutura é particularmente importante. Como tal, em vez da construção de pinos e vigas que se poderia pensar que construiriam as paredes de uma caixa, são utilizados conectores azuis e amarelos para criar os lados. Os conectores azul e amarelo permitem fazer um ângulo reto que fica ao lado do fundo da caixa, e não dentro dela, para que o espaço dentro da caixa tenha um tamanho preciso para acomodar as placas e vigas que irão para dentro. Ambos os lados da caixa são construídos da mesma forma, de modo a que cada caixa base tenha o mesmo tamanho e possa ser utilizada para calcular frações equivalentes dentro da mesma.

As placas e vigas proporcionais encaixam

As placas e vigas do Kit VEX GO estão todas proporcionalmente relacionadas entre si em termos de tamanho e forma e, como tal, ajustam-se de forma precisa (à semelhança dos Blocos Unitários). Isto torna-os manipuladores ideais para explorar as relações entre frações de uma forma tangível. Para além das atividades com a construção de Frações no Laboratório, as vigas e as placas podem ser organizadas e reorganizadas independentemente da construção para ajudar a tornar isto visível para os alunos, o que é uma estratégia útil para aqueles alunos que possam estar a lutar para fazer as ligações .