خلفية
التصور هو استراتيجية تستخدم لمساعدة الطلاب على فهم المفاهيم الرياضية. في هذه الوحدة، سيقوم الطلاب ببناء الكسور لمساعدتهم على تصور الكسور ورؤية العلاقة بين المكافئات الكاملة والمكافئات الكسرية. سيستخدم الطلاب قطع VEX GO لإنشاء تمثيلات مرئية للكسور، بالإضافة إلى التدرب على كتابتها ورسمها بشكل صحيح.
ما هو الكسر؟
الكسر هو تمثيل عددي لأجزاء من الكل. يخبرك البسط بعدد القطع في الكسر، ويشير المقام إلى عدد القطع في الكل. نحن نرى ونستخدم الكسور لمساعدتنا في فهم الأشياء في حياتنا اليومية، من عدد البيتزا التي نطلبها إلى كمية البنزين المتبقية في خزان وقود السيارة. إن فهم كيفية عمل الكسور وارتباطها بالأعداد الصحيحة سيكون مهارة سيبنيها الطلاب أثناء تعلمهم للرياضيات الأكثر تعقيدًا.

لماذا نصور الكسور؟
قد يكون مفهوم تقسيم الرقم إلى أجزاء مجردًا للغاية بحيث يصعب على بعض الطلاب استيعابه. يساعد إنشاء تمثيلات بصرية للكسور على جعلها أكثر واقعية، ويمكّن الطلاب من رؤية الارتباطات بين الأجزاء والكل بشكل أكثر وضوحًا. يمكن القيام بذلك بعدة طرق، من طي الورق، إلى تكديس العناصر المتناسبة أو كتل الوحدة، إلى الرسم والتلوين. كل منها يتيح للطالب رؤية الأجزاء والكل في وقت واحد، حيث يتم تمثيلها بواسطة الكسر. من الأسهل فهم 2/4 = ½ عندما يكون من الواضح أنهما بنفس الحجم.
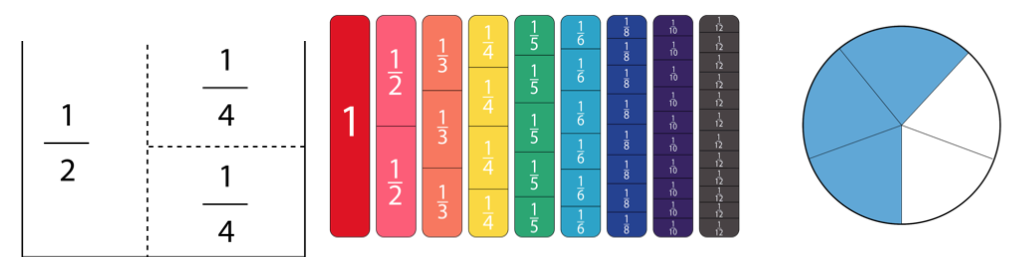
الكسور هي أرقام أيضًا
الكسر هو جزء من عدد، وبالتالي له قيمة عددية وتسلسل، تمامًا مثل الأعداد الصحيحة. نرى تسلسلات من الكسور في كل مرة نستخدم فيها شريط قياس أو ننظر إلى عداد السرعة في السيارة. في بعض الأحيان يقوم الطلاب بفصل القيم الكسرية عن عد الأعداد الصحيحة. وفي هذه الحالة، يواجه الطلاب صعوبات عندما يُطلب منهم إجراء عمليات، مثل الجمع أو الضرب، باستخدام الكسور. يمكن أيضًا تصور الكسور بطريقة متسلسلة. يمكن للطلاب استخدام أدوات التلاعب مثل المسطرة، أو إنشاء خطوط الأعداد الكسرية الخاصة بهم، للمساعدة في فهم وظيفة الكسور في الرياضيات وتطبيقات الحياة الواقعية.
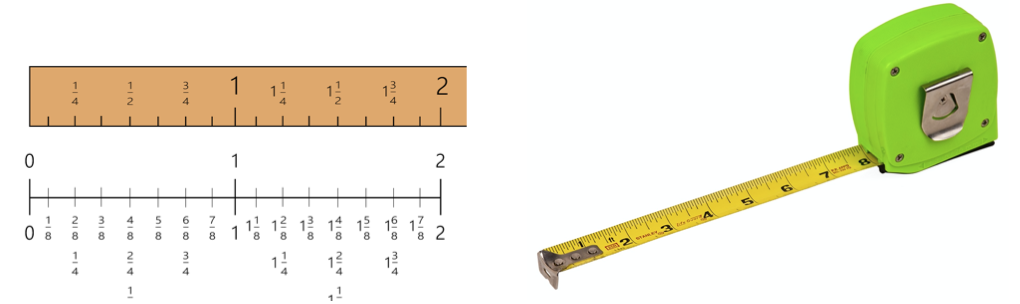
المفاهيم الخاطئة الشائعة حول الكسور

عندما يبدأ الطلاب في بناء فهمهم للكسور، تنشأ بعض المفاهيم الخاطئة بشكل متكرر. ومن المهم تبديد المفاهيم الخاطئة في وقت مبكر، حتى لا تتسبب في مزيد من الارتباك مع تزايد تعقيد العمل.
مفهوم خاطئ: "يجب أن يكون البسط أصغر من المقام".
من السهل أن نرى كيف يمكن للطلاب الوقوع في هذا الفخ، حيث أن الكسور الأولى التي يواجهونها غالبًا تتبع هذا المنطق. إن رؤية الكسور بشكل تسلسلي يمكن أن تساعد الطلاب على تصور هذا على أنه مغالطة. إن تعليم الطلاب أنهم قادرون على العد بالكسور، تمامًا كما يمكنهم العد بالأعداد الصحيحة، أمر مفيد. إن كتابة الأعداد الصحيحة على هيئة كسور (3/1، 6/1، 9/1، إلخ) يمكن أن يساعد في توضيح ذلك، بالإضافة إلى أسئلة مثل "ماذا يأتي بعد 4/4؟" (5/4، 6/4، 7/4، الخ)
مفهوم خاطئ: "يصبح المقام أصغر كلما أصبحت القطع أصغر".
مرة أخرى، قد يبدو هذا منطقيًا إلى حد ما، على الرغم من أن عكسه هو الصحيح بالفعل - فكلما أصبح المقام أصغر، أصبحت القطع أكبر (أو كلما أصبح المقام أكبر، أصبحت القطع أصغر). إن تصور الكسور يمكن أن يبدد هذا المفهوم الخاطئ بسهولة لدى الطلاب، حيث يصبحون قادرين على رؤية والشعور بأحجام القطع فيما يتعلق بالكسور التي تمثلها. إن استخدام قطع مجموعة VEX GO يمكن أن يساعد في جعل هذا الأمر مرئيًا للطلاب بشكل فردي أو كمجموعة، وسيتم تعزيزه طوال فترة هذه الوحدة.
قطع VEX GO
تؤدي الموصلات الزرقاء والصفراء وظيفة محددة
يمكن استخدام الموصلات المختلفة بطرق مختلفة عديدة، وفي هذا البناء، تعد القدرة على بناء جدار على الجانب الخارجي من الهيكل مهمة بشكل خاص. وعلى هذا النحو، بدلاً من بناء الدبابيس والعوارض التي قد تعتقد أنها ستشكل جدران الصندوق، يتم استخدام الموصلات الزرقاء والصفراء لإنشاء الجوانب. تمكن الموصلات الزرقاء والصفراء من عمل زاوية قائمة تقع بجانب الجزء السفلي من الصندوق، بدلاً من داخله، بحيث تكون المساحة داخل الصندوق بحجم دقيق لتناسب الألواح والعوارض التي ستدخل إلى الداخل. يتم إنشاء جانبي الصندوق بنفس الطريقة، بحيث يكون كل صندوق أساسي متساويًا في الحجم، ويمكن استخدامه لتقييم الكسور المكافئة بداخله.

تتناسب الألواح والعوارض المتناسبة مع بعضها البعض
ترتبط جميع الألواح والعوارض في مجموعة VEX GO بشكل متناسب مع بعضها البعض من حيث الحجم والشكل، وبالتالي، تتناسب مع بعضها البعض بطرق دقيقة (على غرار كتل الوحدة). وهذا يجعلها أدوات مثالية لاستكشاف العلاقات بين الكسور بطريقة ملموسة. بالإضافة إلى الأنشطة التي تتضمن بناء الكسور في المختبر، يمكن ترتيب العوارض والألواح وإعادة ترتيبها بشكل مستقل عن البناء للمساعدة في جعل ذلك مرئيًا للطلاب، وهي استراتيجية مفيدة للطلاب الذين قد يواجهون صعوبة في إجراء الاتصالات.
