Sfondo

La visualizzazione è una strategia utilizzata per aiutare gli studenti a comprendere i concetti matematici. In questa Unità, gli studenti realizzeranno la struttura delle Frazioni per aiutarli a visualizzare le frazioni e a vedere le connessioni tra equivalenti interi ed equivalenti frazionari. Utilizzeranno i pezzi VEX GO per creare rappresentazioni visive delle frazioni e per esercitarsi a scriverle e disegnarle correttamente.

Che cosa è una frazione?

Una frazione è una rappresentazione numerica di parti di un intero. Il numeratore indica il numero di pezzi che compongono la frazione, mentre il denominatore indica il numero di pezzi che compongono l'intero. Vediamo e utilizziamo le frazioni per aiutarci a calcolare le cose nella nostra vita quotidiana, dal numero di pizze da ordinare alla quantità di benzina rimasta nel serbatoio di un'auto. Comprendere il funzionamento delle frazioni e la loro relazione con i numeri interi sarà un'abilità che gli studenti rafforzeranno man mano che apprenderanno matematica più complessa.

Perché visualizzare le frazioni?

Il concetto di scomporre un numero in parti può essere troppo astratto perché alcuni studenti possano comprenderlo. Creare rappresentazioni visive delle frazioni le aiuta a diventare più tangibili e consente agli studenti di vedere più chiaramente le connessioni tra le parti e il tutto. Questo può essere fatto in vari modi, piegando la carta, impilando materiali didattici proporzionali o blocchi unitari, fino a disegnare e colorare. Ciascuno di questi metodi consente allo studente di vedere simultaneamente le parti e il tutto rappresentati dalla frazione. È più facile dare un senso alla formula 2/4 = ½ quando è chiaramente visibile che hanno la stessa dimensione.

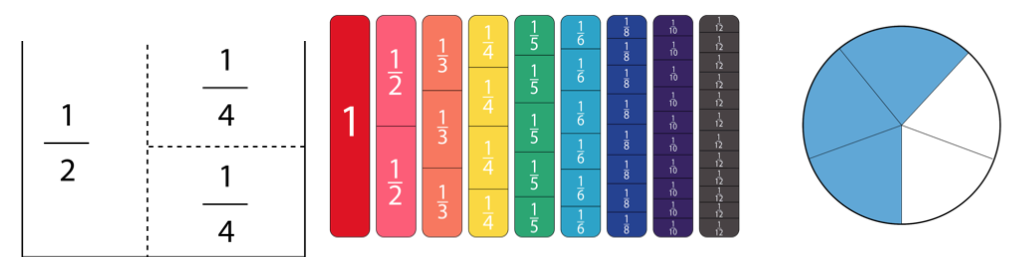
Anche le frazioni sono numeri

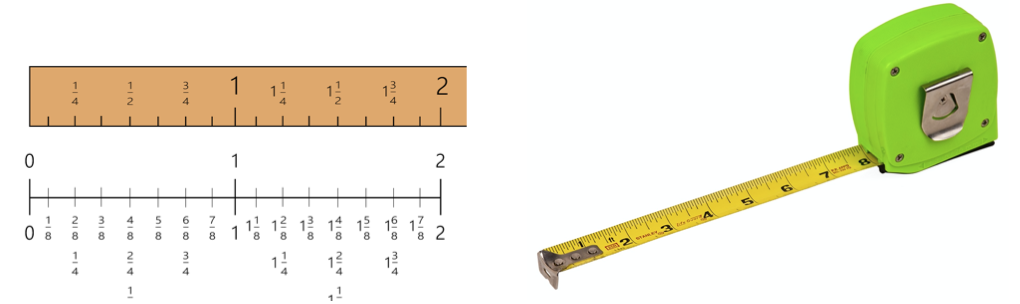
Una frazione è una parte di un numero e come tale ha un valore numerico e una sequenza, proprio come i numeri interi. Ogni volta che utilizziamo un metro a nastro o guardiamo il tachimetro di un'auto, vediamo sequenze di frazioni. A volte gli studenti disgiungono i valori frazionari dal conteggio dei numeri interi. In questo modo, gli studenti incontrano difficoltà quando devono eseguire operazioni con le frazioni, come l'addizione o la moltiplicazione. Le frazioni possono anche essere visualizzate in modo sequenziale. Gli studenti possono utilizzare strumenti come i righelli, oppure creare le proprie rette numeriche frazionarie, per comprendere meglio la funzione delle frazioni in matematica e le applicazioni nella vita reale.

Idee sbagliate comuni sulle frazioni

Quando gli studenti cominciano a comprendere le frazioni, spesso emergono alcuni concetti errati. È importante dissipare i malintesi fin dall'inizio, in modo che non causino ulteriore confusione man mano che il lavoro diventa più complesso.

Idea sbagliata: "Il numeratore deve essere più piccolo del denominatore".
È facile capire come gli studenti possano cadere in questa trappola, poiché le prime frazioni che incontrano spesso seguono questa logica. Osservare le frazioni in sequenza può aiutare gli studenti a visualizzare questa fallacia. È utile insegnare agli studenti che possono contare le frazioni, così come possono contare i numeri interi. Scrivere i numeri interi come frazioni (3/1, 6/1, 9/1, ecc.) può aiutare a chiarire questo concetto, così come rispondere a domande come "Cosa c'è dopo 4/4?" (5/4, 6/4, 7/4, ecc.)

Idea sbagliata: "Il denominatore diventa più piccolo man mano che i pezzi diventano più piccoli".
Di nuovo, questo può sembrare logico fino a un certo punto, anche se in realtà è vero il suo opposto: man mano che il denominatore diventa più piccolo, i pezzi diventano più grandi (o man mano che il denominatore diventa più grande, i pezzi diventano più piccoli). La visualizzazione delle frazioni può facilmente dissipare questo equivoco per gli studenti, poiché possono vedere e sentire le dimensioni dei pezzi in relazione alle frazioni che rappresentano. L'uso dei componenti del kit VEX GO può contribuire a rendere tutto questo visibile agli studenti, individualmente o in gruppo, e verrà rafforzato nel corso di questa Unità.

Pezzi VEX GO

I connettori blu e gialli svolgono una funzione specifica

I vari connettori possono essere utilizzati in molti modi diversi e, in questa costruzione, la capacità di costruire un muro sulla parte esterna della struttura è particolarmente importante. Pertanto, invece dei perni e delle travi che si potrebbe pensare siano necessari per costruire le pareti di una scatola, per creare i lati vengono utilizzati i connettori blu e gialli. I connettori blu e gialli consentono di creare un angolo retto che si trova accanto al fondo della scatola, anziché al suo interno, in modo che lo spazio all'interno della scatola abbia le dimensioni precise per contenere le piastre e le travi che verranno inserite al suo interno. Entrambi i lati della scatola sono costruiti nello stesso modo, in modo che ogni scatola di base abbia le stesse dimensioni e possa essere utilizzata per calcolare le frazioni equivalenti al suo interno.

Piastre e travi proporzionali si adattano insieme

Le piastre e le travi del kit VEX GO sono tutte proporzionalmente correlate tra loro in termini di dimensioni e forma e, come tali, si incastrano tra loro in modo preciso (simile ai blocchi unitari). Ciò li rende strumenti ideali per esplorare concretamente le relazioni tra le frazioni. Oltre alle attività con la costruzione delle frazioni in laboratorio, le travi e le piastre possono essere disposte e riorganizzate indipendentemente dalla costruzione per renderle visibili agli studenti, il che rappresenta una strategia utile per quegli studenti che potrebbero avere difficoltà a stabilire i collegamenti.