Fondo
La visualización es una estrategia utilizada para ayudar a los estudiantes a comprender conceptos matemáticos. En esta unidad, los estudiantes construirán el modelo de fracciones para ayudarlos a visualizar fracciones y ver las conexiones entre equivalentes enteros y equivalentes fraccionarios. Utilizarán piezas VEX GO para crear representaciones visuales de fracciones, así como para practicar cómo escribirlas y dibujarlas correctamente.
¿Qué es una fracción?
Una fracción es una representación numérica de partes de un todo. El numerador indica el número de piezas de la fracción y el denominador indica el número de piezas del total. Vemos y usamos fracciones para ayudarnos a calcular cosas en nuestra vida diaria, desde la cantidad de pizzas que debemos pedir hasta cuánta gasolina queda en el tanque de un automóvil. Comprender cómo funcionan las fracciones y cómo se relacionan con los números enteros será una habilidad que los estudiantes desarrollarán a medida que aprendan matemáticas más complejas.

¿Por qué visualizar fracciones?
El concepto de dividir un número en partes puede ser demasiado abstracto para que algunos estudiantes lo comprendan. La creación de representaciones visuales de fracciones ayuda a que sean más tangibles y permite a los estudiantes ver las conexiones entre las partes y el todo con mayor claridad. Esto se puede hacer de varias maneras, desde doblar papel hasta apilar objetos manipulables proporcionales o bloques unitarios, pasando por dibujar y colorear. Cada uno permite al estudiante ver simultáneamente las partes y el todo representados por la fracción. Es más fácil entender 2/4 = ½ cuando es claramente visible que tienen el mismo tamaño.
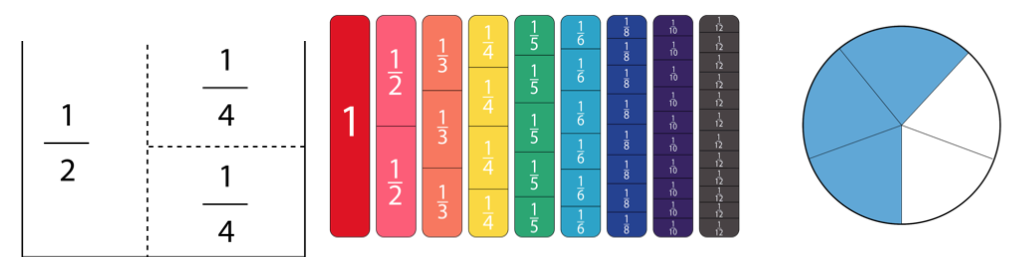
Las fracciones también son números
Una fracción es una parte de un número y, como tal, tiene un valor numérico y una secuencia, tal como lo tienen los números enteros. Vemos secuencias de fracciones cada vez que usamos una cinta métrica o miramos el velocímetro de un automóvil. A veces los estudiantes desconectan los valores fraccionarios del conteo de números enteros. Al hacerlo, los estudiantes tienen dificultades cuando se les pide que realicen operaciones, como suma o multiplicación, con fracciones. Las fracciones también se pueden visualizar de forma secuencial. Los estudiantes pueden usar objetos manipulables como reglas o hacer sus propias líneas de números fraccionarios para ayudar a comprender la función de las fracciones en matemáticas y aplicaciones de la vida real.
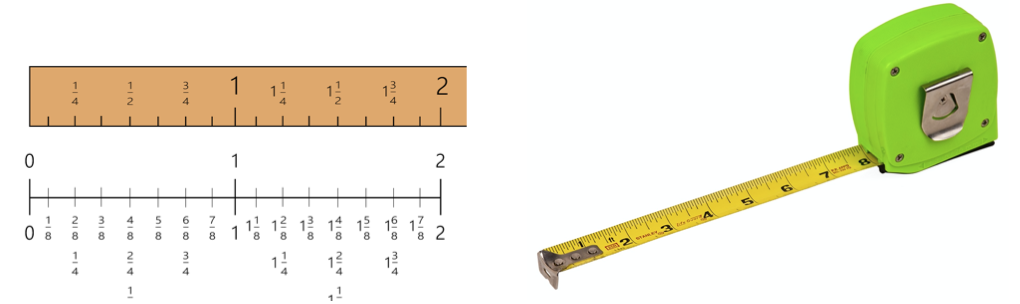
Conceptos erróneos comunes sobre las fracciones

A medida que los estudiantes comienzan a comprender las fracciones, con frecuencia surgen ciertos conceptos erróneos. Es importante disipar los conceptos erróneos desde el principio, para que no causen más confusión a medida que el trabajo se vuelve más complejo.
Idea errónea: “El numerador tiene que ser menor que el denominador”.
Es fácil ver cómo los estudiantes pueden caer en esta trampa, ya que las primeras fracciones que suelen encontrar siguen esta lógica. Ver las fracciones secuencialmente puede ayudar a los estudiantes a visualizar esto como una falacia. Es útil enseñar a los estudiantes que pueden contar en fracciones, tal como pueden hacerlo en números enteros. Escribir números enteros como fracciones (3/1, 6/1, 9/1, etc.) puede ayudar a aclarar esto, así como también preguntas como "¿Qué viene después de 4/4?". (5/4, 6/4, 7/4, etc.)
Idea errónea: “El denominador se hace más pequeño a medida que las piezas se hacen más pequeñas”.
Nuevamente, esto puede parecer lógico hasta cierto punto, aunque en realidad lo opuesto es cierto: a medida que el denominador se hace más pequeño, las piezas se hacen más grandes (o a medida que el denominador se hace más grande, las piezas se hacen más pequeñas). La visualización de fracciones puede disipar fácilmente este concepto erróneo para los estudiantes, ya que pueden ver y sentir los tamaños de las piezas en relación con las fracciones que representan. El uso de piezas del kit VEX GO puede ayudar a que esto sea visible para los estudiantes de forma individual o en grupo, y se reforzará a lo largo de esta unidad.
Piezas de VEX GO
Los conectores azul y amarillo cumplen una función específica
Los distintos conectores se pueden utilizar de muchas maneras diferentes y, en esta construcción, la capacidad de construir una pared en el exterior de una estructura es particularmente importante. Como tal, en lugar de la construcción de pasadores y vigas que podría pensarse que construiría las paredes de una caja, se utilizan los conectores azules y amarillos para crear los lados. Los conectores azules y amarillos permiten hacer un ángulo recto que quede al lado del fondo de la caja, en lugar de dentro de ella, de modo que el espacio dentro de la caja tenga un tamaño preciso para colocar las placas y vigas que irán dentro. Ambos lados de la caja están construidos de la misma manera, de modo que cada caja base tiene el mismo tamaño y puede usarse para evaluar fracciones equivalentes dentro de ella.

Placas y vigas proporcionales encajan entre sí
Las placas y vigas del kit VEX GO están todas relacionadas proporcionalmente entre sí en tamaño y forma y, como tales, encajan entre sí de manera precisa (similar a los bloques unitarios). Esto los convierte en objetos manipulables ideales para explorar las relaciones entre fracciones de una manera tangible. Además de las actividades con la construcción de Fracciones en el Laboratorio, las vigas y las placas se pueden organizar y reorganizar independientemente de la construcción para ayudar a que esto sea visible para los estudiantes, lo que es una estrategia útil para aquellos estudiantes que pueden tener dificultades para hacer las conexiones.
