पृष्ठभूमि

विज़ुअलाइज़ेशन एक रणनीति है जिसका उपयोग छात्रों को गणितीय अवधारणाओं को समझने में मदद करने के लिए किया जाता है। इस इकाई में, विद्यार्थी भिन्नों का निर्माण करेंगे, जिससे उन्हें भिन्नों को देखने में मदद मिलेगी तथा पूर्ण समकक्षों और भिन्नात्मक समकक्षों के बीच संबंध देखने में मदद मिलेगी। वे भिन्नों का दृश्य निरूपण करने के लिए VEX GO टुकड़ों का उपयोग करेंगे, साथ ही उन्हें सही ढंग से लिखने और चित्रित करने का अभ्यास भी करेंगे।

भिन्न क्या है?

भिन्न किसी सम्पूर्ण वस्तु के भागों का संख्यात्मक निरूपण है। अंश आपको भिन्न में टुकड़ों की संख्या बताता है, और हर पूर्ण में टुकड़ों की संख्या बताता है। हम अपने दैनिक जीवन में चीजों को जानने के लिए भिन्नों को देखते हैं और उनका उपयोग करते हैं, चाहे ऑर्डर किए जाने वाले पिज्जा की संख्या हो या कार के गैस टैंक में कितना पेट्रोल बचा है। यह समझना कि भिन्न किस प्रकार कार्य करते हैं और पूर्ण संख्याओं से किस प्रकार संबंधित होते हैं, एक ऐसा कौशल होगा जिसे विद्यार्थी अधिक जटिल गणित सीखते समय विकसित करेंगे।

भिन्नों की कल्पना क्यों करें?

किसी संख्या को भागों में तोड़ने की अवधारणा कुछ विद्यार्थियों के लिए समझने में बहुत कठिन हो सकती है। भिन्नों का दृश्य निरूपण करने से उन्हें अधिक मूर्त बनाने में मदद मिलती है, तथा इससे विद्यार्थियों को भागों और पूर्ण के बीच संबंधों को अधिक स्पष्ट रूप से देखने में मदद मिलती है। यह कई तरीकों से किया जा सकता है, जैसे कागज को मोड़ना, आनुपातिक जोड़तोड़ या इकाई ब्लॉकों को एक के ऊपर एक रखना, चित्र बनाना और रंग भरना। प्रत्येक विद्यार्थी को भिन्न द्वारा दर्शाए गए भागों और पूर्ण को एक साथ देखने में सक्षम बनाता है। 2/4 = ½ को समझना तब आसान होता है जब यह स्पष्ट रूप से दिखाई देता है कि वे एक ही आकार के हैं।

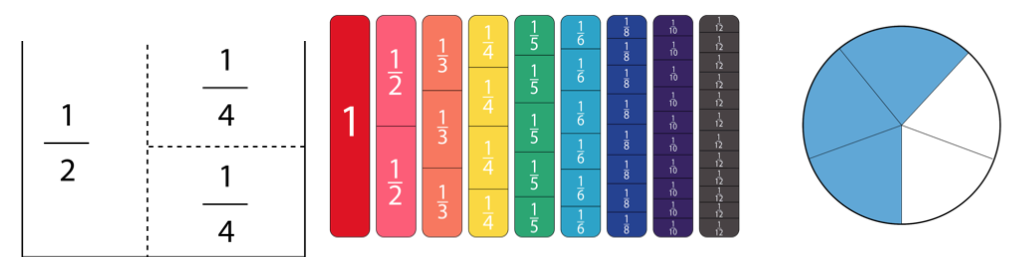
भिन्न भी संख्याएँ हैं

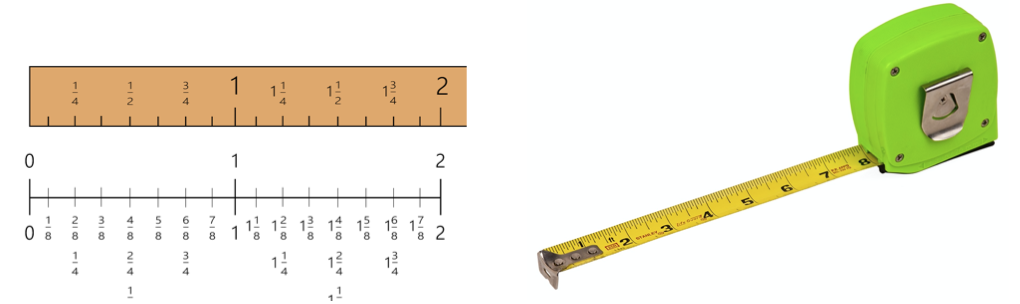
भिन्न किसी संख्या का एक भाग होती है, और इस प्रकार इसका भी एक संख्यात्मक मान और अनुक्रम होता है, ठीक वैसे ही जैसे पूर्ण संख्याओं का होता है। जब भी हम मापने वाले फीते का उपयोग करते हैं या कार के स्पीडोमीटर को देखते हैं तो हमें भिन्नों का क्रम दिखाई देता है। कभी-कभी छात्र पूर्ण संख्या गणना से भिन्नात्मक मानों को अलग कर देते हैं। ऐसा करने में, जब छात्रों से भिन्नों के साथ जोड़ या गुणा जैसी संक्रियाएं करने को कहा जाता है, तो उन्हें कठिनाई होती है। भिन्नों को अनुक्रमिक तरीके से भी देखा जा सकता है। गणित में भिन्नों के कार्य और वास्तविक जीवन के अनुप्रयोगों को समझने में सहायता के लिए विद्यार्थी रूलर जैसे उपकरणों का उपयोग कर सकते हैं, या अपनी स्वयं की भिन्नात्मक संख्या रेखाएं बना सकते हैं।

भिन्नों के बारे में आम गलतफहमियाँ

जैसे-जैसे विद्यार्थी भिन्नों के बारे में समझ विकसित करना शुरू करते हैं, कुछ गलत धारणाएं अक्सर उत्पन्न होने लगती हैं। गलत धारणाओं को शुरू में ही दूर करना महत्वपूर्ण है, ताकि काम जटिल होने पर वे अधिक भ्रम पैदा न करें।

गलत धारणा: “अंश हर से छोटा होना चाहिए।”
यह देखना आसान है कि छात्र इस जाल में कैसे फंस सकते हैं, क्योंकि जिन पहले भिन्नों से वे अक्सर मिलते हैं, वे इसी तर्क का पालन करते हैं। भिन्नों को क्रमिक रूप से देखने से विद्यार्थियों को यह समझने में मदद मिल सकती है कि यह एक भ्रांति है। विद्यार्थियों को यह सिखाना कि वे पूर्ण संख्याओं की तरह भिन्नों में भी गिनती कर सकते हैं, सहायक है। पूर्ण संख्याओं को भिन्नों के रूप में लिखने (3/1, 6/1, 9/1, आदि) से इसे स्पष्ट करने में मदद मिल सकती है, साथ ही "4/4 के बाद क्या आता है?" जैसे प्रश्न भी पूछे जा सकते हैं। (5/4, 6/4, 7/4, आदि)

गलत धारणा: "जैसे-जैसे टुकड़े छोटे होते जाते हैं, हर भी छोटा होता जाता है।"
फिर से, यह कुछ हद तक तर्कसंगत लग सकता है, भले ही इसका विपरीत वास्तव में सच है - जैसे-जैसे हर छोटा होता जाता है, टुकड़े बड़े होते जाते हैं (या जैसे-जैसे हर बड़ा होता जाता है, टुकड़े छोटे होते जाते हैं।) भिन्नों का दृश्यीकरण छात्रों के लिए इस गलत धारणा को आसानी से दूर कर सकता है, क्योंकि वे भिन्नों के संबंध में टुकड़ों के आकार को देखने और महसूस करने में सक्षम होते हैं। VEX GO किट के टुकड़ों का उपयोग करने से छात्रों के लिए व्यक्तिगत रूप से या समूह के रूप में इसे दृश्यमान बनाने में मदद मिल सकती है, और इस इकाई के पूरे पाठ्यक्रम में इसे सुदृढ़ किया जाएगा।

VEX GO टुकड़े

नीले और पीले कनेक्टर एक विशिष्ट कार्य करते हैं

विभिन्न कनेक्टरों का उपयोग कई अलग-अलग तरीकों से किया जा सकता है, और इस निर्माण में, संरचना के बाहर दीवार बनाने की क्षमता विशेष रूप से महत्वपूर्ण है। इस प्रकार, आप सोच सकते हैं कि पिन और बीम निर्माण से बॉक्स की दीवारें बनाई जाएंगी, लेकिन नीले और पीले कनेक्टर का उपयोग किनारों को बनाने के लिए किया जाता है। नीले और पीले कनेक्टर एक समकोण बनाने में सक्षम बनाते हैं जो बॉक्स के अंदर की बजाय नीचे की ओर होता है, ताकि बॉक्स के अंदर का स्थान प्लेटों और बीमों को फिट करने के लिए एक सटीक आकार का हो जो अंदर जाएंगे। बॉक्स के दोनों किनारों का निर्माण एक ही तरीके से किया जाता है, ताकि प्रत्येक आधार बॉक्स का आकार बराबर हो, और इसका उपयोग इसके अंदर समतुल्य भिन्नों का मूल्यांकन करने के लिए किया जा सके।

आनुपातिक प्लेटें और बीम एक साथ फिट होते हैं

VEX GO किट की प्लेटें और बीम सभी आकार और आकृति में एक दूसरे से आनुपातिक रूप से संबंधित हैं, और इस प्रकार, सटीक तरीके से एक साथ फिट होते हैं (यूनिट ब्लॉक के समान)। यह उन्हें भिन्नों के बीच संबंधों को मूर्त रूप में तलाशने के लिए आदर्श साधन बनाता है। लैब में फ्रैक्शंस निर्माण के साथ गतिविधियों के अलावा, बीम और प्लेटों को निर्माण से स्वतंत्र रूप से व्यवस्थित और पुनर्व्यवस्थित किया जा सकता है ताकि छात्रों को यह दिखाई दे सके, जो उन छात्रों के लिए एक उपयोगी रणनीति है जो कनेक्शन बनाने में संघर्ष कर रहे हैं।

पर स्पष्ट रूप से दिखाई देती है