Arrière-plan
La visualisation est une stratégie utilisée pour aider les élèves à comprendre les concepts mathématiques. Dans cette unité, les élèves construiront le modèle Fractions pour les aider à visualiser les fractions et à voir les liens entre les équivalents entiers et les équivalents fractionnaires. Ils utiliseront les pièces VEX GO pour créer des représentations visuelles de fractions, ainsi que pour s'entraîner à les écrire et à les dessiner correctement.
Qu'est-ce qu'une fraction ?
Une fraction est une représentation numérique de parties d’un tout. Le numérateur indique le nombre de pièces dans la fraction et le dénominateur indique le nombre de pièces dans le tout. Nous voyons et utilisons des fractions pour nous aider à comprendre les choses dans notre vie quotidienne, du nombre de pizzas à commander à la quantité d'essence restante dans le réservoir d'une voiture. Comprendre comment les fractions fonctionnent et se rapportent aux nombres entiers sera une compétence que les élèves développeront à mesure qu’ils apprendront des mathématiques plus complexes.

Pourquoi visualiser les fractions ?
Le concept de division d’un nombre en parties peut être trop abstrait pour que certains élèves puissent le comprendre. Créer des représentations visuelles des fractions les aide à devenir plus tangibles et permet aux élèves de voir plus clairement les liens entre les parties et le tout. Cela peut être fait de plusieurs manières, depuis le pliage de papier jusqu'à l'empilement d'objets manipulables proportionnels ou de blocs unitaires, en passant par le dessin et le coloriage. Chacun permet à l’élève de voir simultanément les parties et le tout représentés par la fraction. Il est plus facile de comprendre 2/4 = ½ lorsqu'il est clairement visible qu'ils ont la même taille.
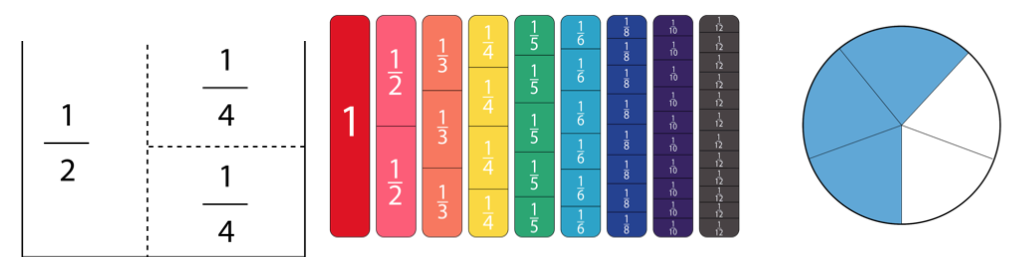
Les fractions sont aussi des nombres
Une fraction est une partie d'un nombre et, en tant que telle, possède une valeur et une séquence numériques, tout comme les nombres entiers. Nous voyons des séquences de fractions chaque fois que nous utilisons un ruban à mesurer ou que nous regardons le compteur de vitesse d’une voiture. Parfois, les élèves déconnectent les valeurs fractionnaires du comptage des nombres entiers. Ce faisant, les élèves éprouvent des difficultés lorsqu’on leur demande d’effectuer des opérations, comme l’addition ou la multiplication, avec des fractions. Les fractions peuvent également être visualisées de manière séquentielle. Les élèves peuvent utiliser des objets manipulables comme des règles ou créer leurs propres lignes de nombres fractionnaires pour les aider à comprendre la fonction des fractions en mathématiques et les applications de la vie réelle.
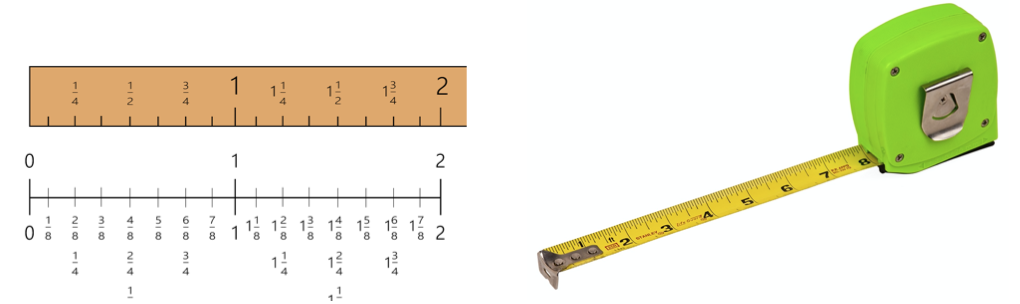
Idées fausses courantes sur les fractions

À mesure que les élèves commencent à comprendre les fractions, certaines idées fausses surgissent fréquemment. Il est important de dissiper les idées fausses dès le début, afin qu’elles ne créent pas davantage de confusion à mesure que le travail devient plus complexe.
Idée fausse : « Le numérateur doit être plus petit que le dénominateur. »
Il est facile de comprendre comment les élèves peuvent tomber dans ce piège, car les premières fractions qu’ils rencontrent suivent souvent cette logique. Voir les fractions de manière séquentielle peut aider les élèves à visualiser cela comme une erreur. Il est utile d’apprendre aux élèves qu’ils peuvent compter en fractions, tout comme ils peuvent compter en nombres entiers. Écrire des nombres entiers sous forme de fractions (3/1, 6/1, 9/1, etc.) peut aider à clarifier cela, ainsi que des questions telles que « Que vient après 4/4 ? » (5/4, 6/4, 7/4, etc.)
Idée fausse : « Le dénominateur devient plus petit à mesure que les pièces deviennent plus petites. »
Encore une fois, cela peut sembler logique dans une certaine mesure, même si son contraire est en fait vrai : à mesure que le dénominateur devient plus petit, les pièces deviennent plus grandes (ou à mesure que le dénominateur devient plus grand, les pièces deviennent plus petites). La visualisation des fractions peut facilement dissiper cette idée fausse pour les élèves, car ils sont capables de voir et de sentir la taille des pièces en relation avec les fractions qu’elles représentent. L'utilisation des pièces du kit VEX GO peut aider à rendre cela visible pour les étudiants individuellement ou en groupe, et sera renforcée tout au long de cette unité.
Pièces VEX GO
Les connecteurs bleus et jaunes remplissent une fonction spécifique
Les différents connecteurs peuvent être utilisés de nombreuses manières différentes, et dans cette construction, la possibilité de construire un mur à l'extérieur d'une structure est particulièrement importante. Ainsi, au lieu de la construction à broches et à poutres que vous pourriez penser qui permettrait de construire les parois d'une boîte, les connecteurs bleus et jaunes sont utilisés pour créer les côtés. Les connecteurs bleus et jaunes permettent de réaliser un angle droit qui se trouve à côté du fond de la boîte, plutôt qu'à l'intérieur de celle-ci, de sorte que l'espace à l'intérieur de la boîte soit d'une taille précise pour s'adapter aux plaques et aux poutres qui iront à l'intérieur. Les deux côtés de la boîte sont construits de la même manière, de sorte que chaque boîte de base est de taille égale et peut être utilisée pour évaluer les fractions équivalentes à l'intérieur.

Les plaques et les poutres proportionnelles s'assemblent
Les plaques et les poutres du kit VEX GO sont toutes proportionnellement liées les unes aux autres en termes de taille et de forme et, en tant que telles, s'assemblent de manière précise (de manière similaire aux blocs unitaires). Cela en fait des objets de manipulation idéaux pour explorer les relations entre les fractions de manière tangible. En plus des activités avec la construction Fractions dans le laboratoire, les poutres et les plaques peuvent être disposées et réorganisées indépendamment de la construction pour aider à rendre cela visible pour les élèves, ce qui est une stratégie utile pour les élèves qui peuvent avoir du mal à établir les connexions.
