Mathe-Unterstützung
Beim Unterrichten der Übungen 4 und 5 werden zusätzliche mathematische Konzepte und Berechnungen vermittelt. Diese Seite bietet Lehrern relevante Hintergrundressourcen zur Unterstützung der Mathematik, die die Schüler in diesen Laboren erforschen.
Mathematik des Fahrens
Um die Parade in Labor 4 abzuschließen, fahren die Schüler mit ihrem Code Base-Festwagen eine gerade
Paradestrecke entlang. Anstatt Antriebsblöcke zu verwenden, die beide Räder gleichzeitig bewegen, verwenden
die Schüler wie hier gezeigt die Blöcke [Drehen für] in VEXcode GO, um die mit den Rädern verbundenen
Motoren zu drehen und den Roboter vorwärts zu bewegen. [Spin for]-Blöcke akzeptieren ‚Drehungen‘ oder ‚Grad‘
als Parameter. In Übung 4 berechnen die Schüler die Anzahl der Kurven, die sie in dieses Projekt eingeben
müssen, um ihren Roboter die Distanz der Paradestrecke zurückzulegen.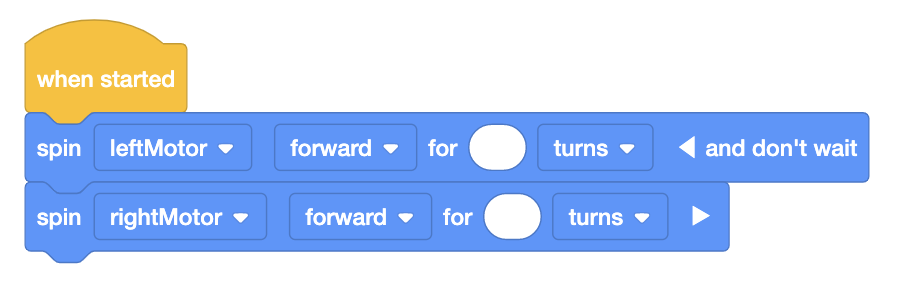
Sehen Sie sich das Video unten an, um zu erfahren, wie Sie die Anzahl der Radumdrehungen berechnen, die erforderlich sind, um Ihren Roboter über eine festgelegte Distanz geradeaus zu fahren.
Hilfreiche Referenzen:
Terminologie und Werte für die grauen Räder:
| Begriff | Definition | Visuell | Formel | Wert |
|---|---|---|---|---|
| Durchmesser | Messung einer geraden Linie durch den Mittelpunkt eines Kreises | 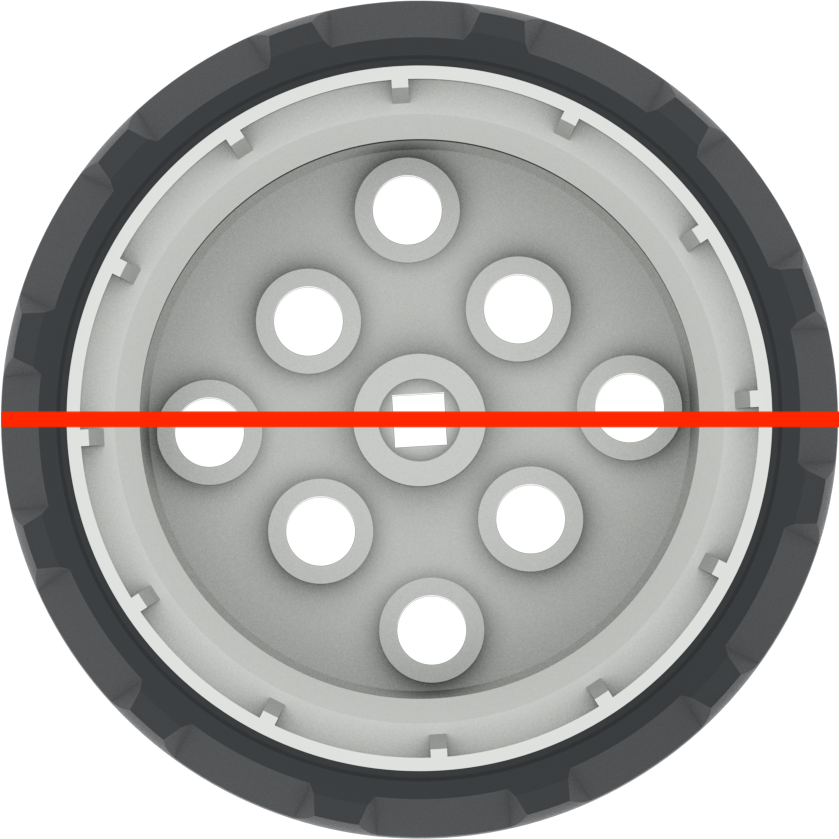 |
d = 2 r | ~ 50,93 mm oder 2 Zoll |
| Umfang | Die Gesamtentfernung um die Außenseite eines Kreises |  |
C = π d | ~ 160 mm oder 6,25 Zoll |
Genau messen
Wenn die Schüler Messungen durchführen, weisen Sie sie unbedingt an, sorgfältig und präzise zu messen. Sie können verwendendas druckbare VEX GO-Linealfür Schüler zum Ausmessen oder Lineale im Klassenzimmer.
- Erinnern Sie die Schüler daran, mit der Messung am Nullpunkt des Lineals zu beginnen, und genau auf den Endpunkt des zu messenden Objekts zu achten. Wenn Sie Ihre Messungen ungenau beginnen oder beenden, wirkt sich dies auf ihre Berechnungen und die letztendliche Bewegung ihres Roboters aus.
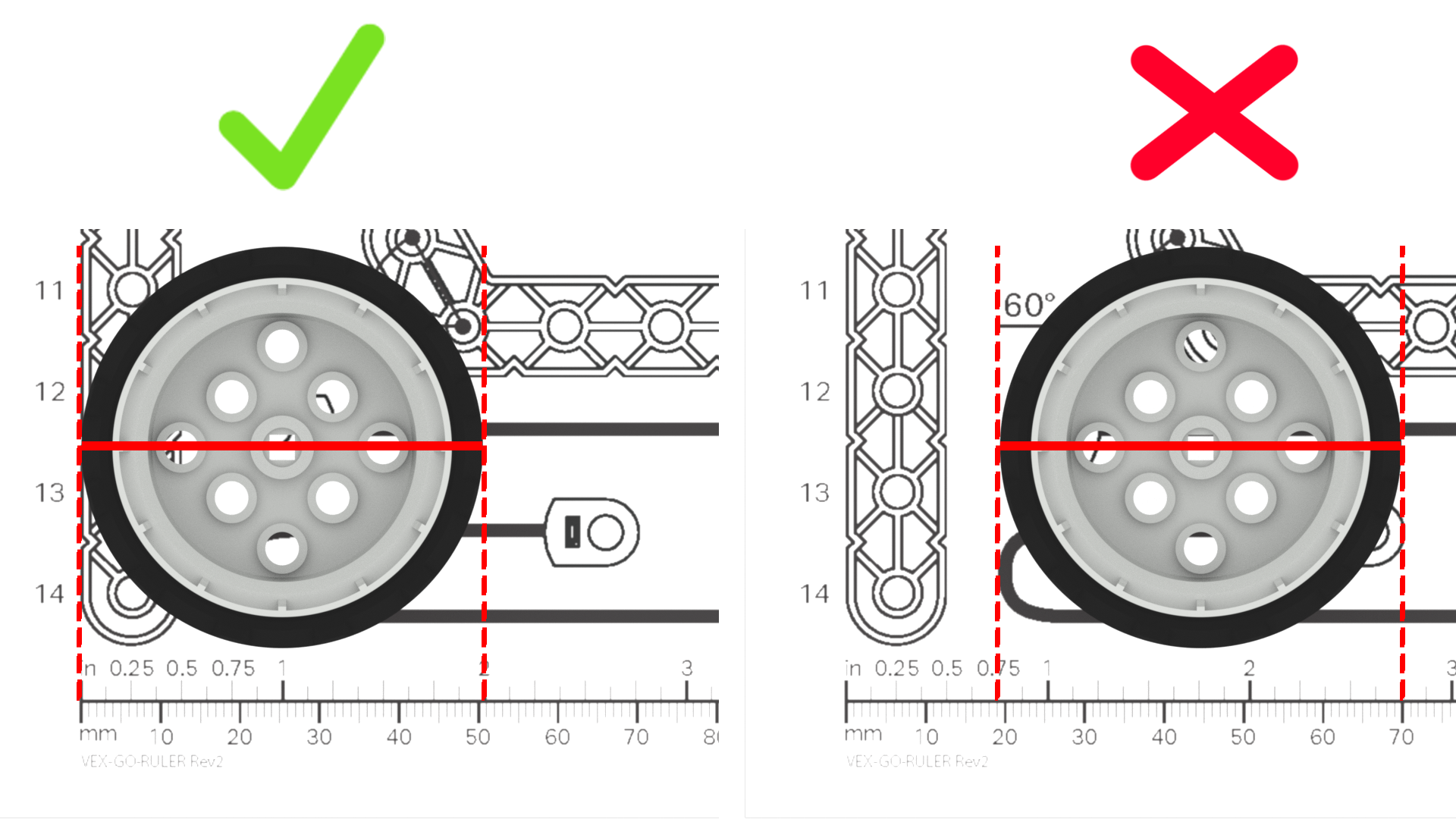
- Stellen Sie sicher, dass die Schüler wissen, wie sie die Markierungen auf dem von ihnen verwendeten Lineal lesen müssen, um genau messen zu können. Wenn die von Ihnen verwendeten Lineale dies haben sowohl imperiale als auch metrische Einheiten (wie der VEX GO Druckbares Lineal)Stellen Sie sicher, dass die Schüler stets dieselben Maßeinheiten verwenden.
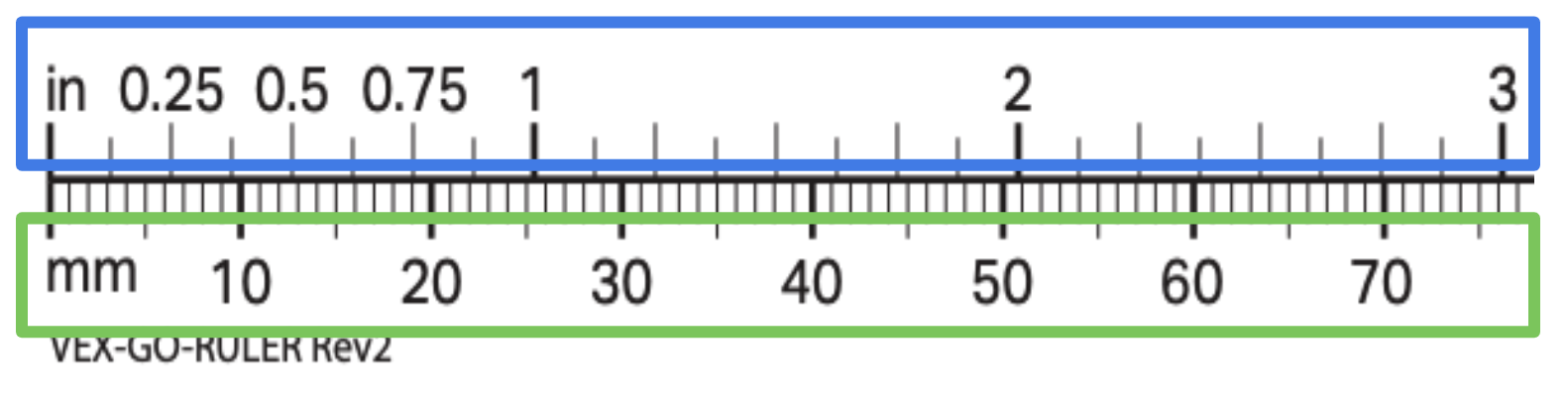
- Die Schüler dürfen ihre Messungen auf die nächste Einheit, oder den Bruchteil einer Einheit runden. Durch Runden können Berechnungen bei Bedarf vereinfacht werden, es kann jedoch auch zu einer ungenaueren Messung führen. Sie können Ihren Schülern beispielsweise sagen, sie sollen auf den nächsten halben Zoll oder Zentimeter aufrunden, doch ihr Roboter bewegt sich etwas weiter als ursprünglich beabsichtigt. Alternativ können Sie die Schüler auf ⅛ Zoll oder Millimeter genau messen lassen und feststellen, dass ihre Roboter näher an der beabsichtigten Distanz herankommen.
- Wenn die Schüler zusätzliche Übung beim Messen benötigen, Sie können das verwenden Üben Messung der VEX GO-Aktivität mit einzelnen Schülern oder Gruppen oder als Aktivität für die ganze Klasse.
Mathematik der 360°-Drehung
Um die Parade in Labor 5 abzuschließen, fahren die Schüler mit ihrem Code Base-Festwagen mit einer Kurve entlang einer Paraderoute.
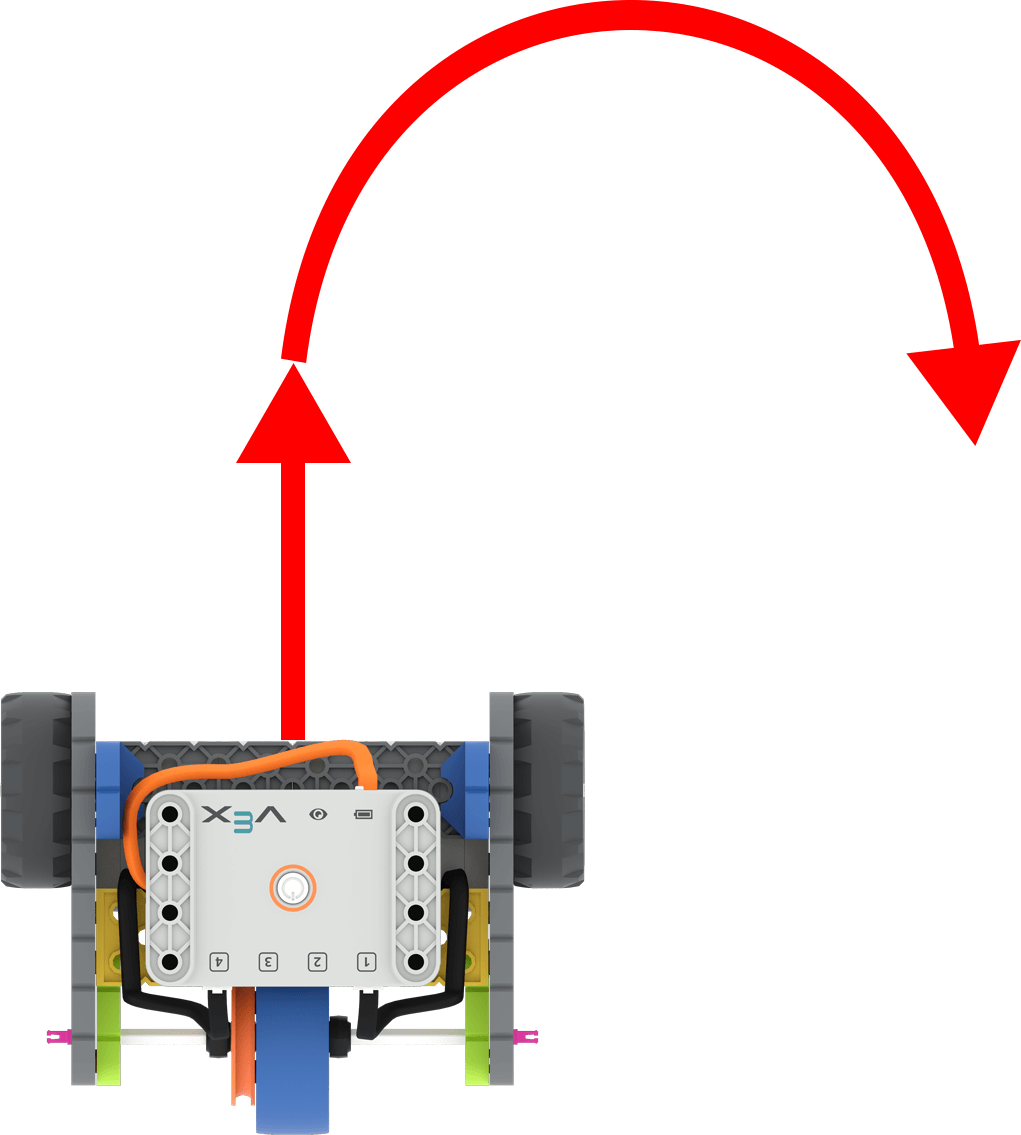
Codebasis mit Pfeilen, die das Vorwärtsfahren und anschließende Rechtsabbiegen anzeigen
Die Schüler bauen auf dem auf, was sie über die Programmierung des Roboters zum Zurücklegen einer geraden
Strecke und zum Befahren einer nichtlinearen Strecke oder einer Kurve gelernt haben. Die Schüler berechnen
immer noch die Anzahl der Umdrehungen, die zum Zurücklegen einer bestimmten Distanz erforderlich sind. Sie
verwenden daher dieselbe Formel wie im vorherigen Labor.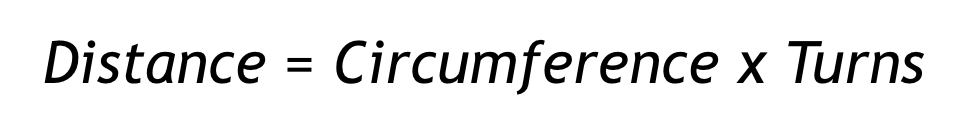
Sehen Sie sich das Video unten an, um zu erfahren, wie Sie mit Ihren Schülern die Anzahl der Radumdrehungen berechnen, die erforderlich sind, um mit dem Roboter eine° auszuführen.
Hilfreiche Referenzen:
Wenn sich die Code Base dreht, bewegen sich die Antriebsräder in entgegengesetzte Richtungen, um den Roboter zu drehen. Um den Roboter beispielsweise nach rechts zu wenden, fährt das linke Rad vorwärts, während das rechte Rad rückwärts fährt.
Terminologie und Werte für die Codebasis:
| Begriff | Definition | Visuell | Formel | Wert |
|---|---|---|---|---|
| Durchmesser | Messung einer geraden Linie von der Mitte jedes Rades (auch Radstand genannt) |  |
d = 2 r | ~ 135 mm oder 5,3 Zoll |
| Umfang | Die Gesamtstrecke, die die Räder zurücklegen, um eine 360°-Drehung zu vollenden | 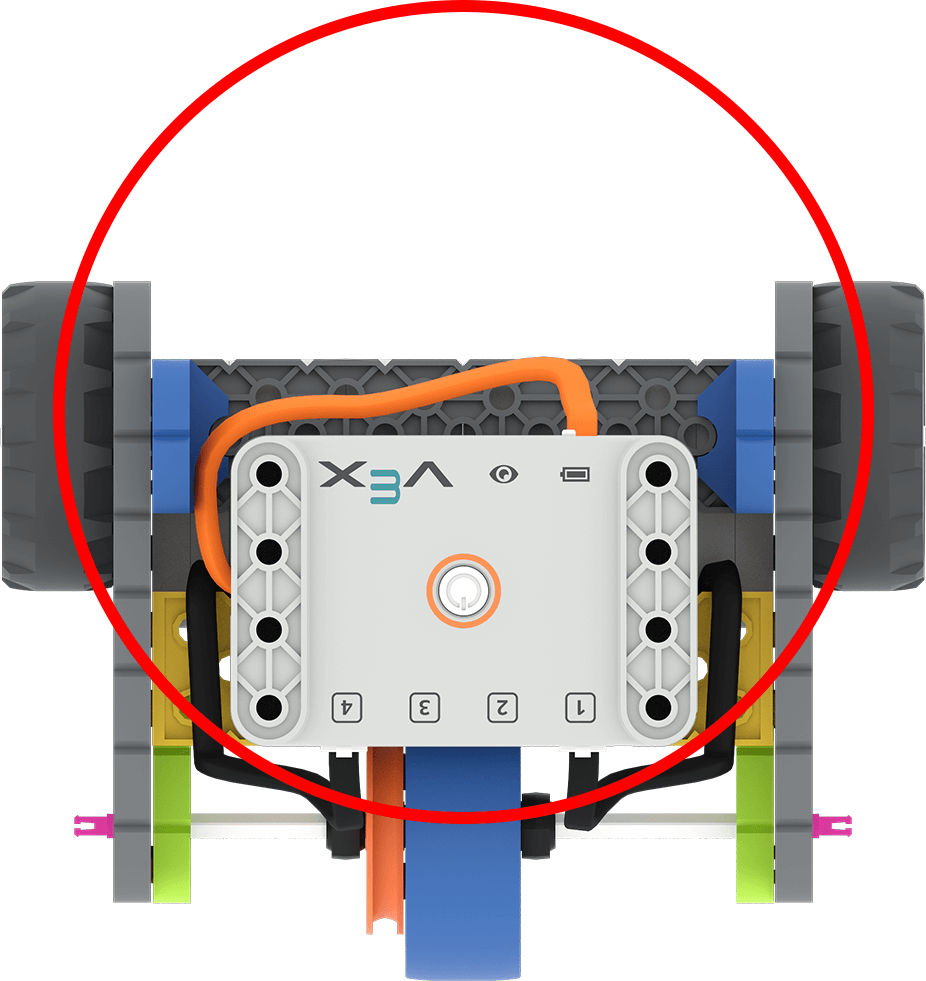
|
C = π d | ~ 424 mm oder 16,7 Zoll |
Mathematik zum Drehen eines beliebigen Grades
Sehen Sie sich dieses Video an, um mehr über die Berechnung der Anzahl der Radumdrehungen zu erfahren, die der Roboter benötigt, um sich um einen beliebigen Grad zu drehen.
Umrechnen in Grad
Der Block [Drehen für] akzeptiert Drehungen oder Grad als Parameter.
Um Gradangaben zu verwenden, multiplizieren Sie einfach die Anzahl der Umdrehungen mit 360. Dieses Beispiel
zeigt die Anzahl der Grad, um die sich die Motoren drehen müssen, um den Roboter um volle 360° zu
drehen. Beachten Sie, dass sich in diesem Projekt die Motoren in entgegengesetzte Richtungen
drehen und dass „und nicht warten“ zum ersten Block hinzugefügt wird, sodass sich die Motoren gleichzeitig
drehen. Dadurch wird der Roboter um die gewünschten 360° nach rechts gedreht. 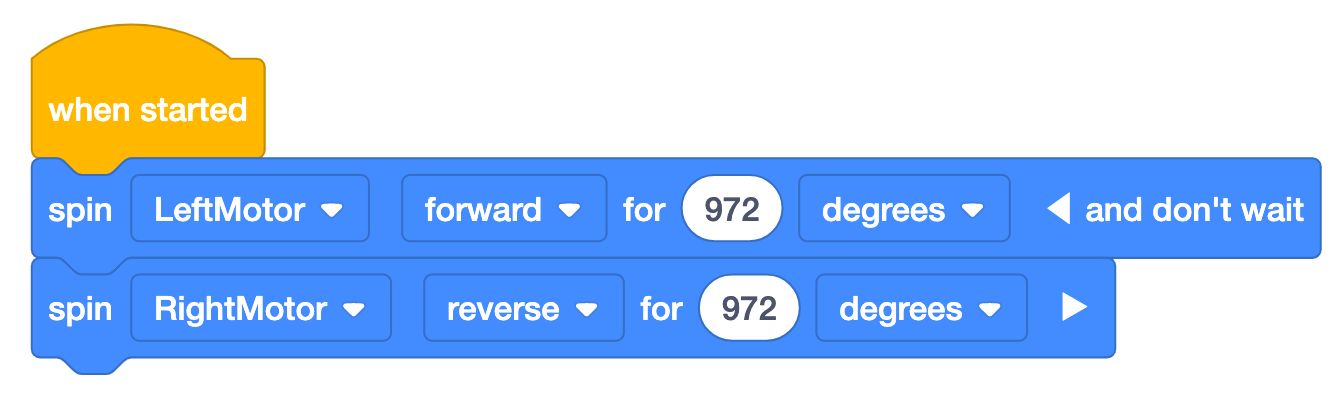
Häufige Missverständnisse
Schüler können beim Messen und bei der Mathematik des Fahrens und Wenden viele falsche Vorstellungen haben. Dies sind einige der häufigsten, mit Vorschlägen, wie Sie sie mit Ihren Schülern ansprechen können.
| Situation | Missverständnis | Vorgeschlagene Korrektur |
|---|---|---|
|
Der Lehrer fragt die Klasse: „Was müssen wir in den Block [Drehen für] eingeben, damit sich der Roboter um 90° dreht?“ Der Student antwortet „90“. |
Die Distanz in Grad, die das Rad zurücklegt, um eine Kurve zu fahren, entspricht dem Drehwinkel. Die Schüler verwenden den Wendeumfang des Roboters nicht, um die Distanz in Grad zu berechnen, die das Rad zurücklegen muss. |
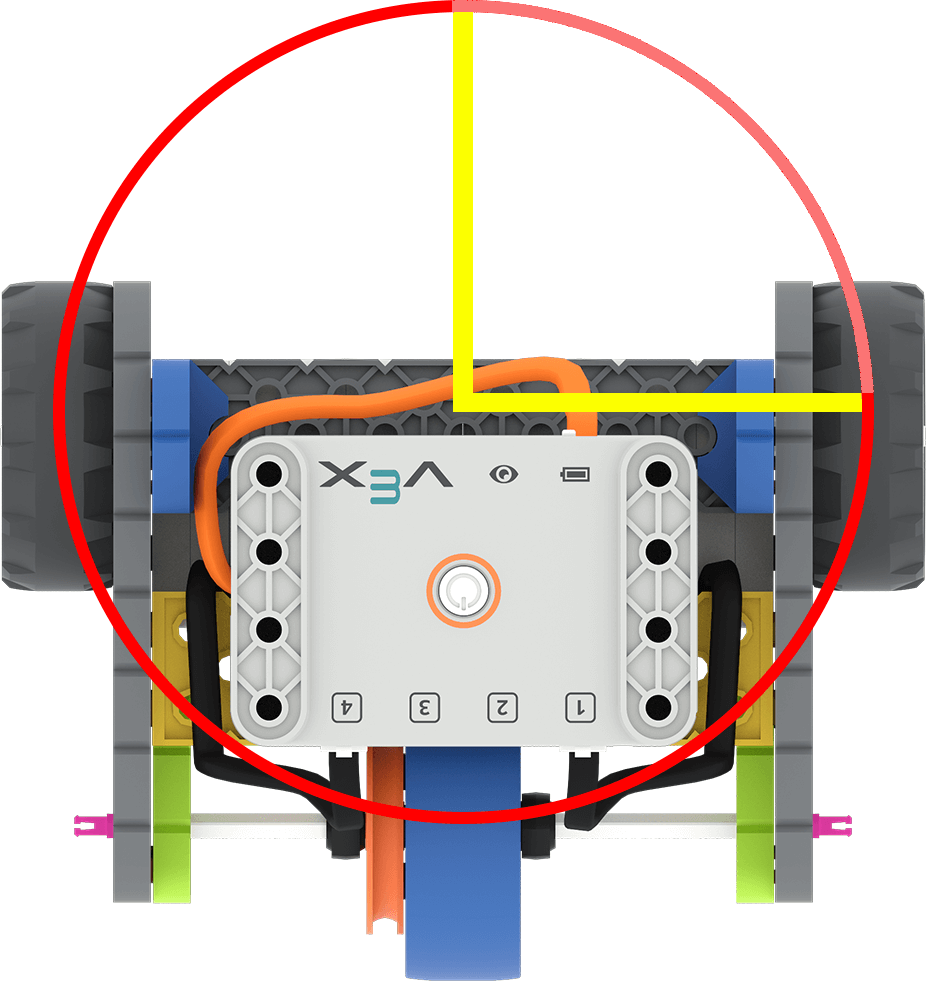
Erinnern Sie die Schüler daran, dass die Räder entlang des Wendekreises fahren müssen, damit der Roboter wenden kann. (In diesem Bild verläuft das entlang des roten Kreises von einer gelben Linie zur anderen.)
Drehen Sie das Rad selbst nur um 90°, damit die Schüler sich besser vorstellen können, wie weit sich das Rad dreht, um eine bestimmte Strecke zurückzulegen. |
|
Der Lehrer fragt die Klasse: „Was müssen wir in den Block [Drehen für] eingeben, damit der Roboter 12 Zoll vorwärts fährt?“ Der Schüler antwortet „12“. |
Die Anzahl der Radumdrehungen entspricht der gewünschten Fahrstrecke. Der Schüler berechnet anhand des Radumfangs nicht die Anzahl der Radumdrehungen, die zum Zurücklegen der gewünschten Distanz erforderlich sind. |
Erinnern Sie die Schüler daran, wie weit sich der Roboter mit einer Radumdrehung bewegt, und fragen Sie, ob 12 vollständige Umdrehungen für eine Strecke von 12 Zoll zu viel oder zu wenig erscheinen. Damit sich die Schüler dies besser vorstellen können, rollen Sie ein Rad 12 Umdrehungen lang über ein Lineal, um den Schülern zu zeigen, wie weit diese Distanz ist.
Erinnern Sie die Schüler daran, dass eine Radumdrehung dem Radumfang entspricht und dass 12 Zoll durch diesen Umfang geteilt werden müssen. |
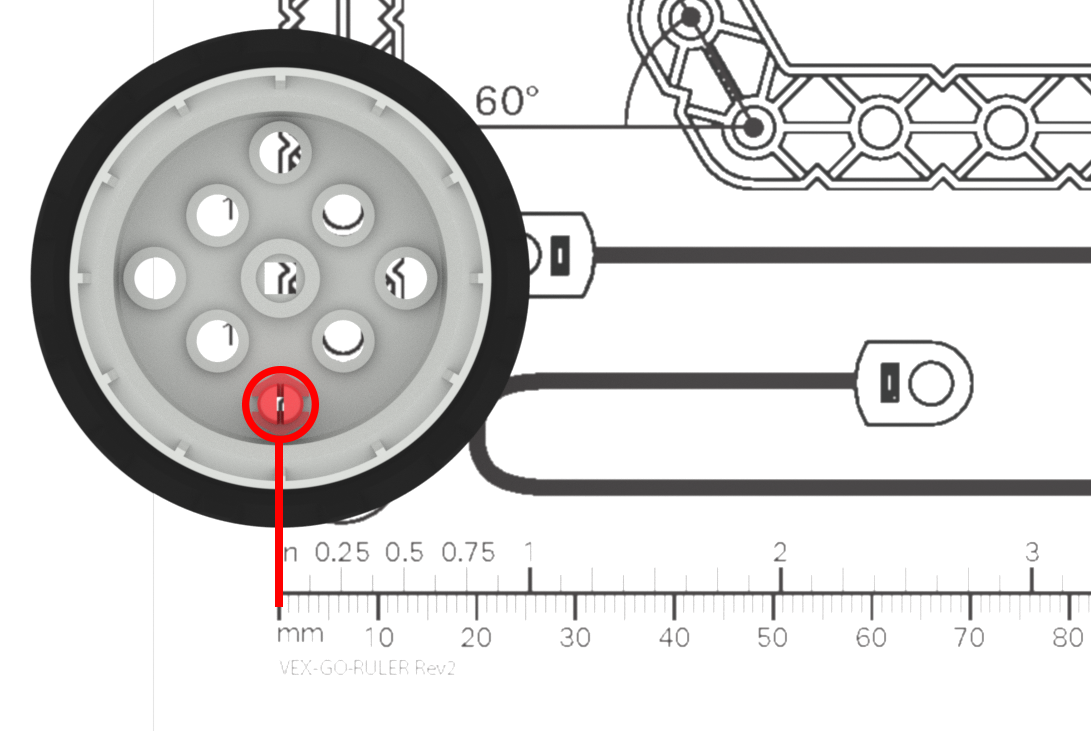
| Der Schüler misst das Rad, aber keine Kante des Rades befindet sich auf der Nullmarkierung des Lineals. |
Das Lineal beginnt bei 1, nicht bei Null. Der Schüler verwendet das Lineal nicht richtig, um eine genaue Messung zu erhalten. |
Erinnern Sie die Schüler daran, dass das Lineal bei der Markierung „0“ beginnt und dass ihre Messungen falsch sind, wenn sie nicht von diesem Punkt aus messen. Sie können den Anfang des Lineals mit Klebeband oder einem farbigen Stift markieren, um den Schülern während der Arbeit eine zusätzliche visuelle Hilfe zu bieten. (Für zusätzliches Üben mit Messen, Schüler können die abschließen Üben Aktivität messen.) |
|
Ein Student sagt, sein Projekt funktioniert nicht. Der Lehrer bemerkt, dass im Block [Drehen für] die richtige Anzahl an Radumdrehungen steht, der Parameter jedoch auf „Grad“ eingestellt ist. |
Einheiten bzw. Parameter sind austauschbar. Die Studierenden achten in ihrem Projekt nicht auf die Parameter/Maßeinheiten. |
Fragen Sie die Schüler, welche Maßeinheit sie verwenden und ob diese mit dem Parameter im Block übereinstimmt.
|
| Ein Schüler versucht, in den Parameter des Blocks [Drehen für] „21/4“ einzugeben, um „2 ¼ Umdrehungen“ einzugeben. |
Brüche und Dezimalzahlen werden auf die gleiche Weise geschrieben. Der Schüler wandelt den Bruch nicht in eine Dezimalzahl um. |
Erinnern Sie die Schüler daran, dass sie Brüche in Dezimalzahlen umwandeln müssen, damit sie
erkennbare Parameter darstellen. Teilen Sie hierzu den Zähler durch den Nenner. 2 ¼=94 =2,25 Sie können Ihre Schüler dazu anregen, häufig verwendete Bruchwerte und deren Dezimaläquivalente in einem Diagramm darzustellen, um so eine eigene Ressource zu erstellen. |
|
Der Lehrer bittet die Schüler, ihre Berechnung des Radumfangs mitzuteilen. Antworten der Schüler |
Der Umfang wird mit dem Radius berechnet -πxRadius. Der Schüler verwendet bei der Berechnung die falsche Maßeinheit. |
Erinnern Sie die Schüler daran, dass der Umfang beträgt π x
Durchmesser; und der Durchmesser ist eine gerade Linie durch die Mitte
des Rades (oder das Doppelte des Radius).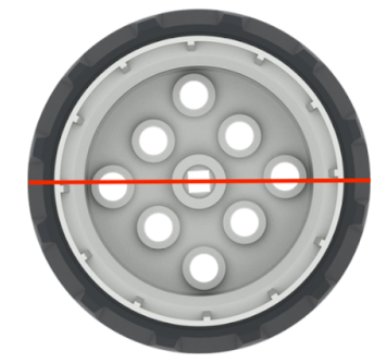 Möglicherweise möchten Sie den Wert einer gesamten Klassenaktivität messen und berechnen wenn viele Schüler Schwierigkeiten mit der Anwendung der Formeln haben. |
Beispiellösungen
Labor 4 Beispiellösung
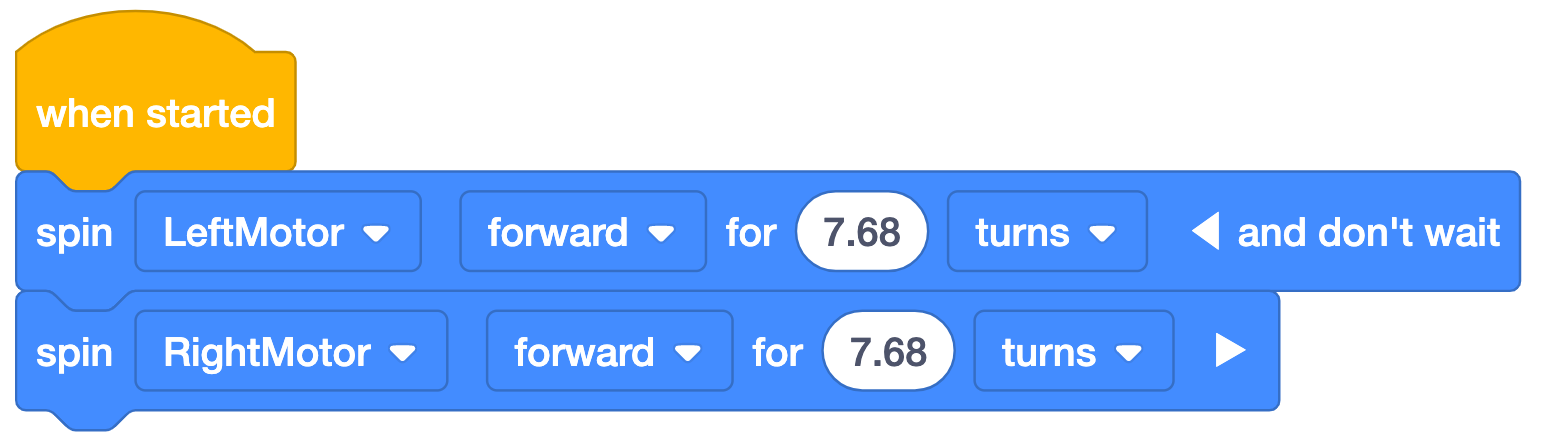
*Hinweis: „und nicht warten“ wird mit dem ersten Block im Beispielprojekt verwendet, sodass beide Blöcke gleichzeitig ausgeführt werden. Ohne „und nicht warten“ würde sich zuerst der Motor drehen, dann der zweite, und die Codebasis würde nicht wie vorgesehen laufen. Stellen Sie sicher, dass die Schüler das „Und warten Sie nicht“-Prinzip NICHT abbrechen, da ihr Projekt sonst nicht wie vorgesehen läuft.

Um die 48 Zoll (~122 cm) lange Paradestrecke zu fahren, muss die Code Base ~7,68 Kurven
fahren. Links ist die Berechnung dargestellt, rechts die Beispiellösung von VEXcode GO.
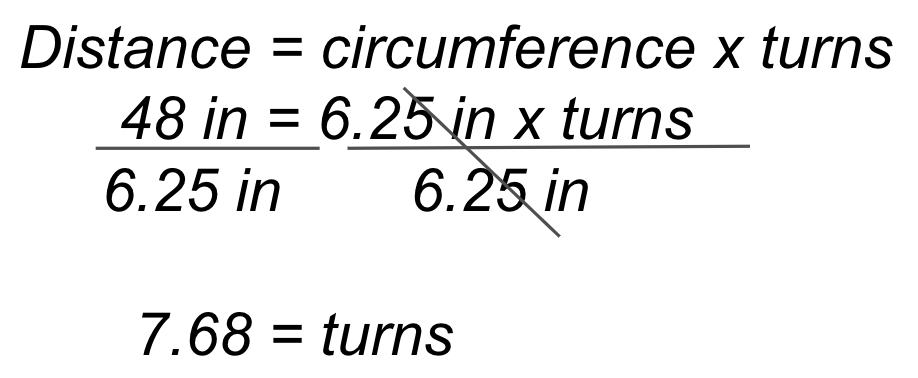
Labor 5 Beispiellösung
Um die 48 Zoll (~122 cm) lange Paradestrecke zu fahren und eine 180-Grad-Wende zu vollführen, muss die Code Base ca. 7,68 Umdrehungen vorwärts fahren, dann einen Motor vorwärts und den anderen rückwärts , und zwar ca. 1,47 Umdrehungen. Die Berechnung wird rechts neben der Beispiellösung VEXcode GO angezeigt.
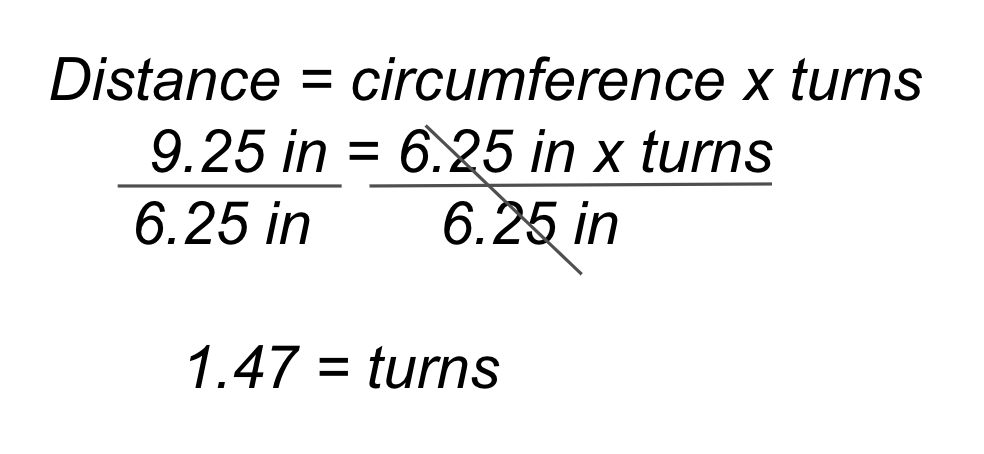

Hinweis: Um Gradangaben statt Drehungen zu verwenden, multiplizieren
Sie bei der Drehberechnung mit 360.
Erweiterung Paradestrecke
Wenn die Schüler eine zusätzliche Herausforderung brauchen, können Sie die Paradestrecke auf viele verschiedene Arten verlängern. Dies ist ein Beispiel mit einer möglichen Lösung.
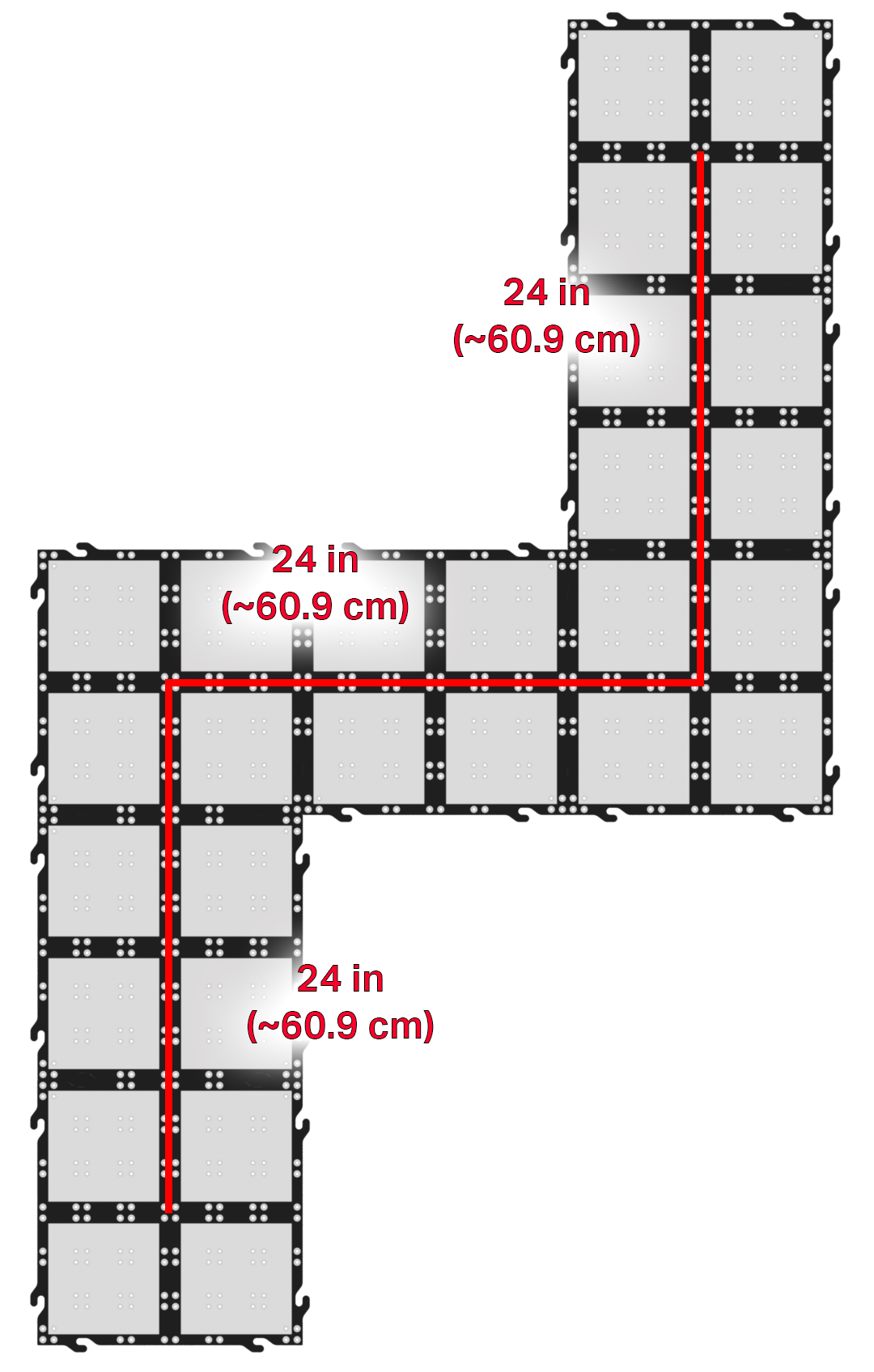
Auf dieser Beispielroute werden die Fahrstrecken und Abbiegungen im Vergleich zu den Labs halbiert. Bei
dieser Route ist jedoch die Richtung der Kurven wichtig. Zusätzlich zum Neurechnen müssen die Schüler
herausfinden, in welche Richtung die Räder gedreht werden müssen, um sie in die gewünschte Richtung zu
drehen.
Die halbierten Berechnungen aus den vorherigen Übungen lauten wie folgt:
Fahrstrecke = ~ 3,84 Umdrehungen
Wendestrecke = ~ 0,73 Umdrehungen
Diese Werte werden in der folgenden Beispiellösung von VEXcode GO verwendet:
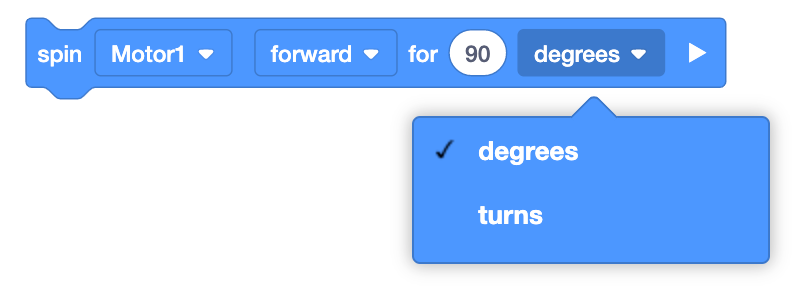 Erinnern Sie die Schüler daran, dass ihre Berechnungen nur dann wie
vorgesehen funktionieren, wenn der Parameter auf die richtige Einheit eingestellt ist. Drehungen
und Grade haben nicht denselben Wert.
Erinnern Sie die Schüler daran, dass ihre Berechnungen nur dann wie
vorgesehen funktionieren, wenn der Parameter auf die richtige Einheit eingestellt ist. Drehungen
und Grade haben nicht denselben Wert.