Supporto matematico

Durante l'insegnamento dei laboratori 4 e 5, vengono coinvolti ulteriori concetti matematici e calcoli. Questa pagina offre agli insegnanti risorse di base utili a supportare la matematica che gli studenti esplorano in questi laboratori.

Matematica della guida

Per completare la sfilata nel Lab 4, gli studenti guideranno il loro carro Code Base lungo un percorso rettilineo. Invece di utilizzare blocchi di trasmissione che muovono entrambe le ruote contemporaneamente, gli studenti utilizzeranno i blocchi [Spin for] in VEXcode GO, come mostrato qui, per far girare i motori collegati alle ruote e far avanzare il robot. I blocchi [Spin for] accettano 'giri' o 'gradi' come parametri. Nel laboratorio 4, gli studenti calcoleranno il numero di svolte da inserire nel progetto per guidare il loro robot lungo la distanza del percorso della parata.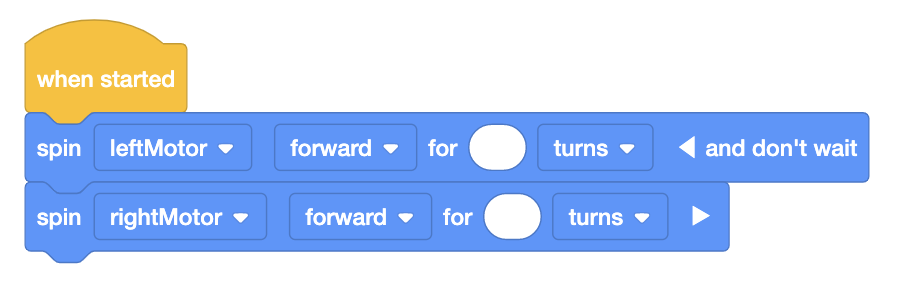 Un progetto VEXcode GO inizia con un blocco When started e ha due blocchi Spin for associati con il parametro distance vuoto. I blocchi riportano la scritta "Una volta avviato, far girare il motore sinistro in avanti per curve a vuoto e non aspettare; quindi far girare il motore destro in avanti per curve a vuoto".

Guarda il video qui sotto per scoprire come calcolare il numero di giri della ruota necessari per far muovere il tuo robot in linea retta per una determinata distanza.

Riferimenti utili:

Terminologia e valori per le ruote grigie:

Termine	Definizione	Visivo	Formula	Valore
Diametro	Misurazione di una linea retta attraverso il centro di un cerchio		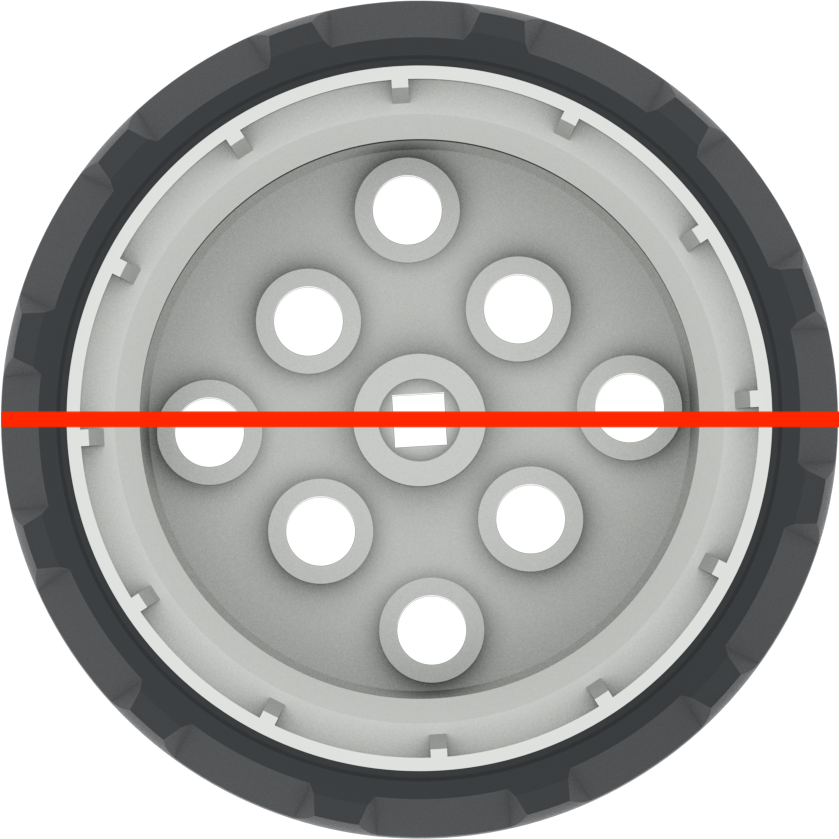d = 2 r	~ 50,93 mm o 2 pollici
Circonferenza	La distanza totale attorno all'esterno di un cerchio		C = πd	~ 160 mm o 6,25 pollici

Misurazione accurata

Quando gli studenti effettuano le misurazioni, assicuratevi di guidarli affinché misurino con attenzione e precisione. Puoi usare il VEX GO stampabile Governate per consentire agli studenti di misurare o ai righelli della classe.

Ricordare agli studenti di iniziare la misurazione dal punto zero sul righello e di prestare molta attenzione al punto finale dell'oggetto che stanno misurando. Iniziare o terminare le misurazioni in modo non accurato influirà sui calcoli e sul movimento finale del robot.

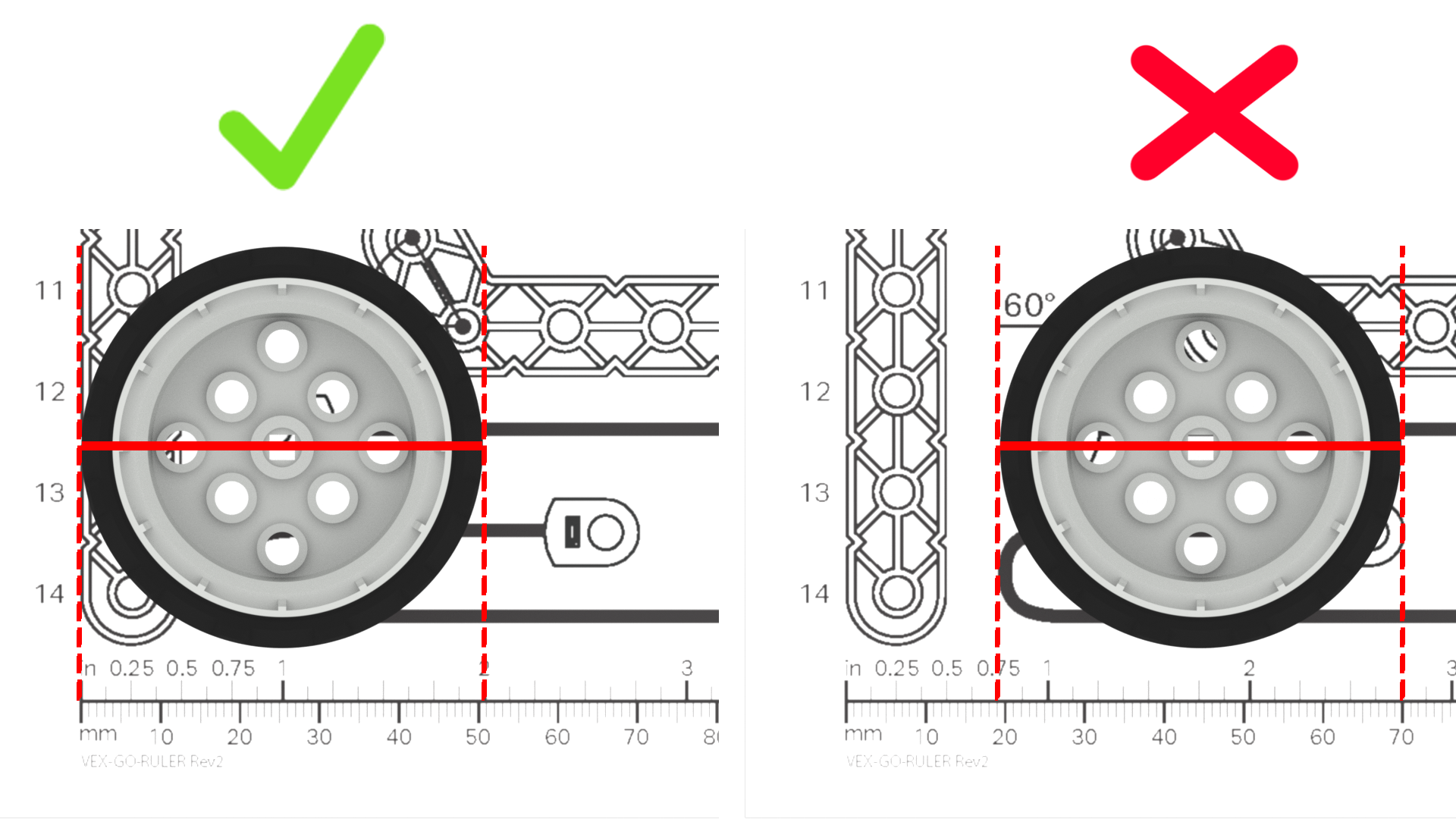
Uno schema indica come allineare con precisione una ruota VEX GO sul righello stampabile. Sul lato sinistro, un segno di spunta verde indica il corretto allineamento: la ruota è appoggiata sul righello, con una linea rossa che indica il diametro e linee tratteggiate che indicano l'allineamento del bordo sinistro e destro della ruota con il segno 0 del righello e circa 50 mm. A destra, una x rossa indica un allineamento non corretto: vengono mostrate la stessa ruota e le stesse linee, ma il righello è contrassegnato a circa 19 e 70 mm. — Una ruota GO mostrata allineata correttamente e in modo non corretto sul righello VEX GO

Assicuratevi che gli studenti sappiano come leggere i segni sul righello che stanno utilizzando, per poter misurare con precisione. Se i righelli che stai utilizzando hanno entrambi i gradi imperiali e unità metriche (es il VEX GO stampabile Governate)assicurarsi che gli studenti utilizzino costantemente le stesse unità di misura.

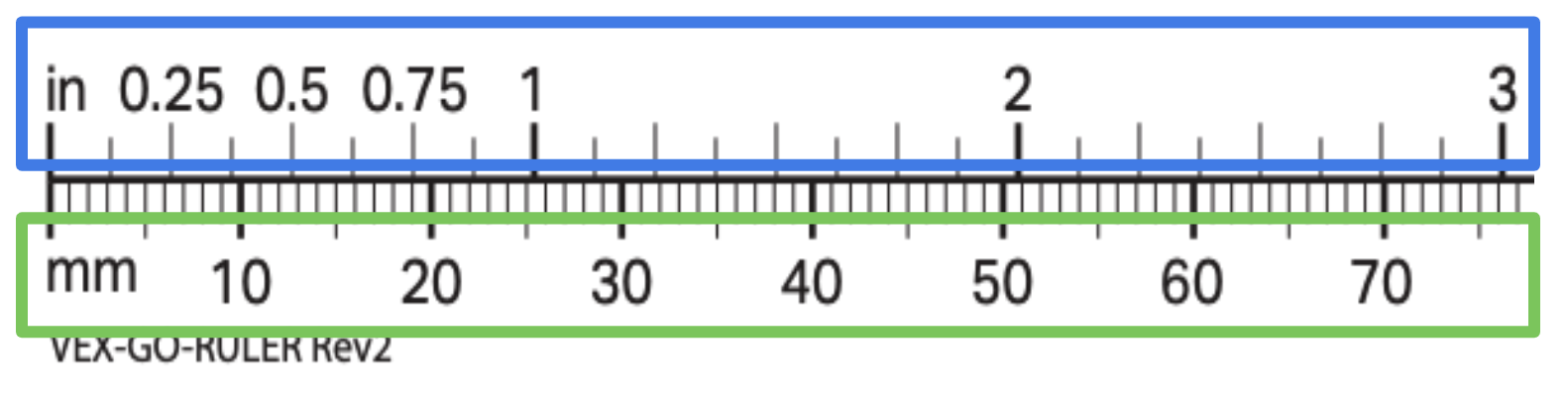
Righello stampabile VEX GO con unità imperiali evidenziate in blu e unità metriche evidenziate in verde

Gli studenti possono arrotondare le loro misure all'unità più vicina, o a una frazione di unità. Se necessario, l'arrotondamento può semplificare i calcoli, ma può anche rendere le misurazioni meno precise. Ad esempio, potresti chiedere agli studenti di arrotondare al mezzo pollice o centimetro più vicino, ma il loro robot si sposterà leggermente più lontano di quanto inizialmente previsto. In alternativa, puoi chiedere agli studenti di misurare la distanza con un'approssimazione di ⅛ di pollice o di millimetro e di scoprire che i loro robot si spostano più vicino alla distanza prevista.
If students need extra practice with measuring, you can use the Practice Measuring VEX GO Activity with individual students or groups, or as a whole class activity.

Matematica della rotazione di 360°

Per completare la sfilata nel Lab 5, gli studenti guideranno il loro carro Code Base lungo un percorso della sfilata con una curva.

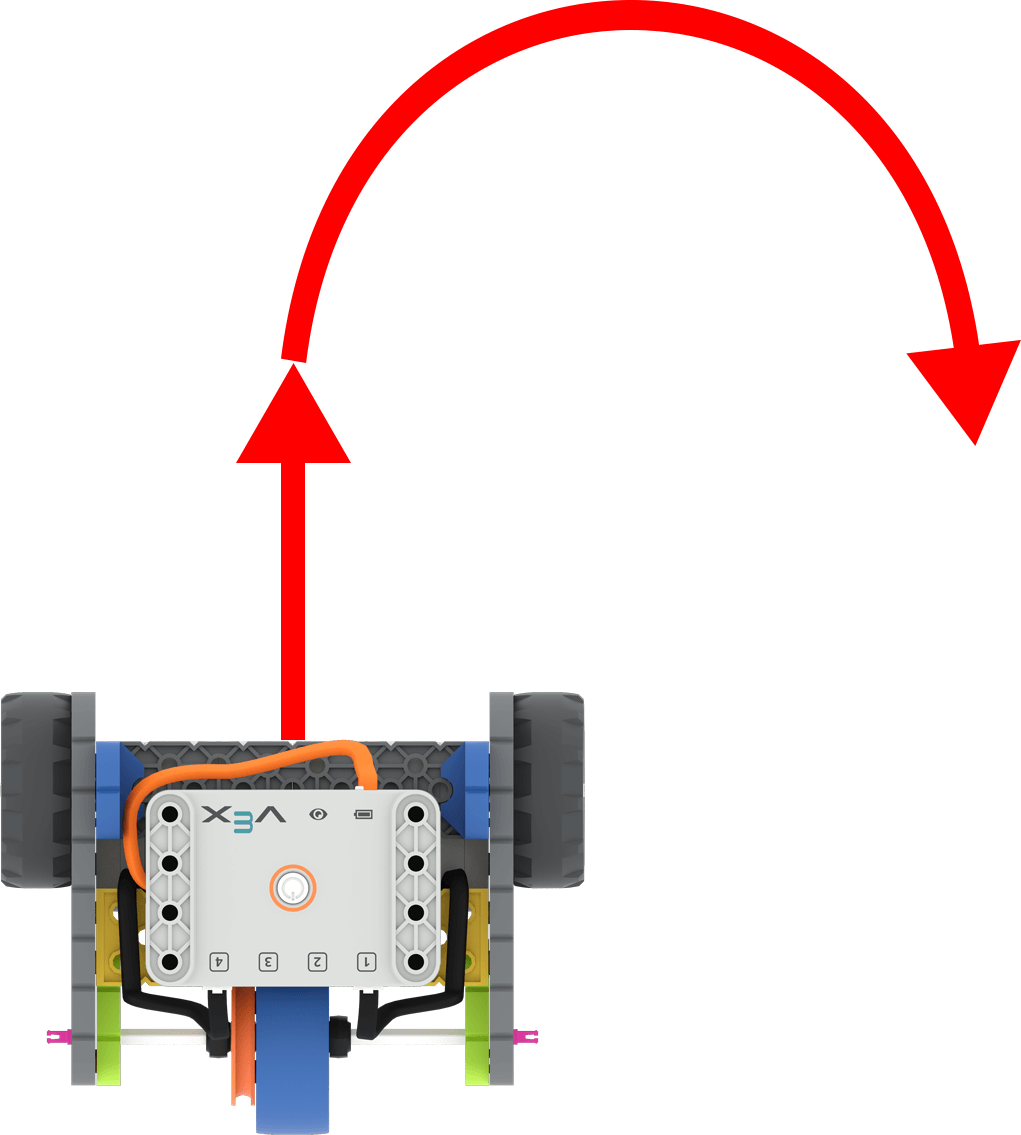
Codice base con una freccia che si estende dalla parte anteriore del robot, per indicare i movimenti di guida in avanti e successiva svolta a destra.

Codice base con frecce per mostrare la guida in avanti e poi la svolta a destra

Gli studenti svilupperanno quanto appreso sulla programmazione del robot per percorrere una distanza in linea retta, per percorrere una distanza non lineare o per svoltare. Gli studenti stanno ancora calcolando il numero di svolte necessarie per percorrere una determinata distanza, quindi useranno la stessa formula del laboratorio precedente.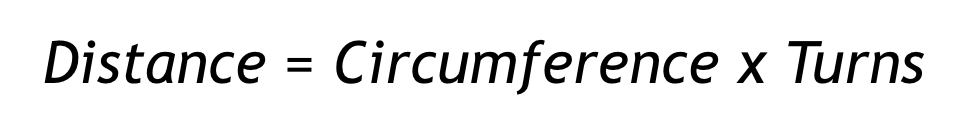 La formula recita "distanza uguale circonferenza moltiplicata giri".

Guarda il video qui sotto per scoprire insieme ai tuoi studenti come calcolare il numero di giri delle ruote necessari per far compiere al robot un giro di°.

Riferimenti utili:

Quando la base di codice gira, le ruote motrici si muovono in direzioni opposte per far girare il robot. Ad esempio, per girare il robot verso destra, la ruota sinistra andrà in avanti, mentre quella destra andrà in retromarcia.

Terminologia e valori per la base di codice:

Termine	Definizione	Visivo	Formula	Valore
Diametro	Misurazione di una linea retta dal centro di ciascuna ruota (noto anche come passo)		d = 2 r	~ 135 mm o 5,3 pollici
Circonferenza	La distanza totale percorsa dalle ruote per completare un giro di 360°		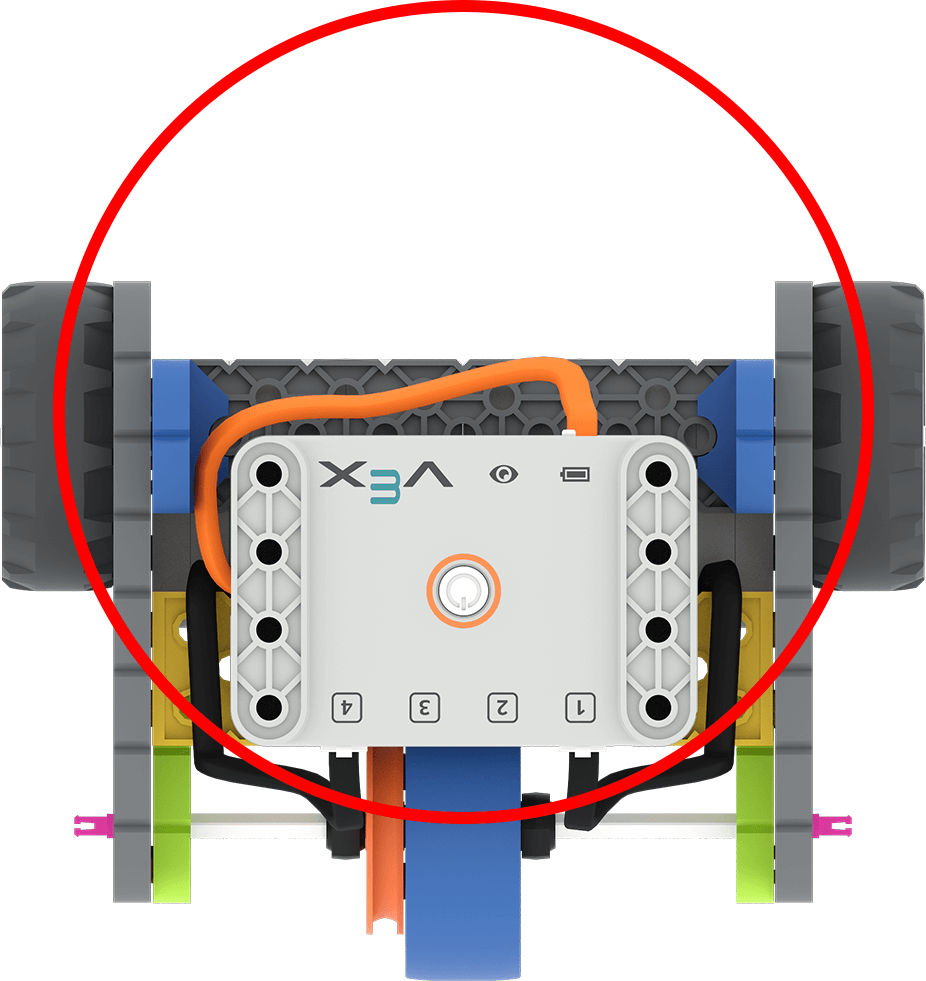C = πd	~ 424 mm o 16,7 pollici

Matematica per ruotare qualsiasi grado

Guarda questo video per saperne di più sul calcolo del numero di giri della ruota necessari al robot per girare di qualsiasi grado.

Conversione in gradi
Il blocco [Spin for] accetterà giri o gradi come parametri. Per usare i gradi, basta moltiplicare il numero di giri per 360. Questo esempio mostra di quanti gradi ruoteranno i motori per far ruotare il robot di°. Si noti che in questo progetto i motori girano in direzioni opposte e che "e non aspettare" viene aggiunto al primo blocco, quindi i motori girano simultaneamente. In questo modo il robot ruoterà verso destra per i 360° desiderati. 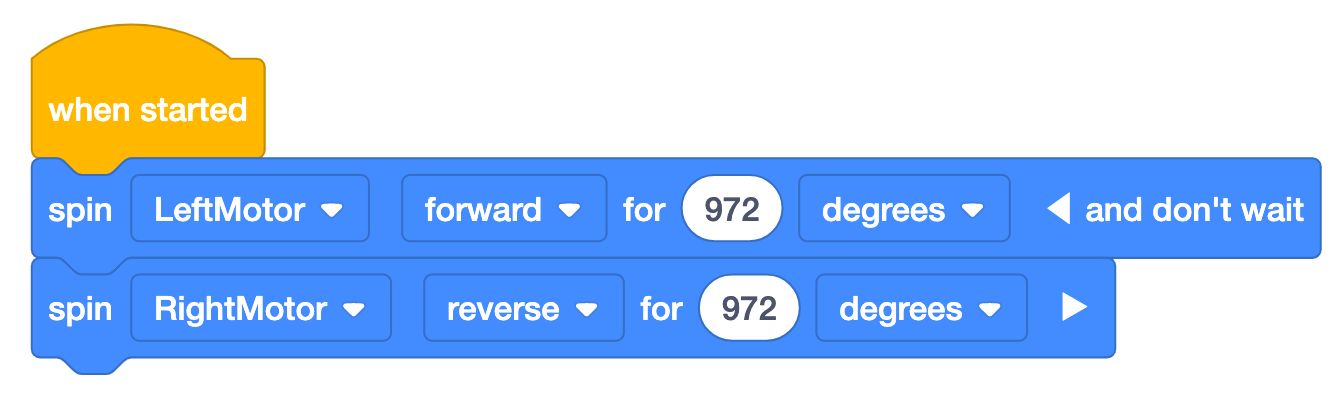Il progetto VEXcode GO inizia con un blocco When started con due blocchi Spin for allegati. I blocchi riportano la scritta "Una volta avviato, far girare il motore sinistro in avanti per 972 gradi e non aspettare; quindi far girare il motore destro all'indietro per 972 gradi".

Idee sbagliate comuni

Ci sono diversi equivoci che gli studenti possono avere riguardo alle misurazioni e alla matematica della guida e delle svolte. Ecco alcuni dei più comuni, con suggerimenti su come affrontarli con i tuoi studenti.

Situazione	Idea sbagliata	Correzione suggerita
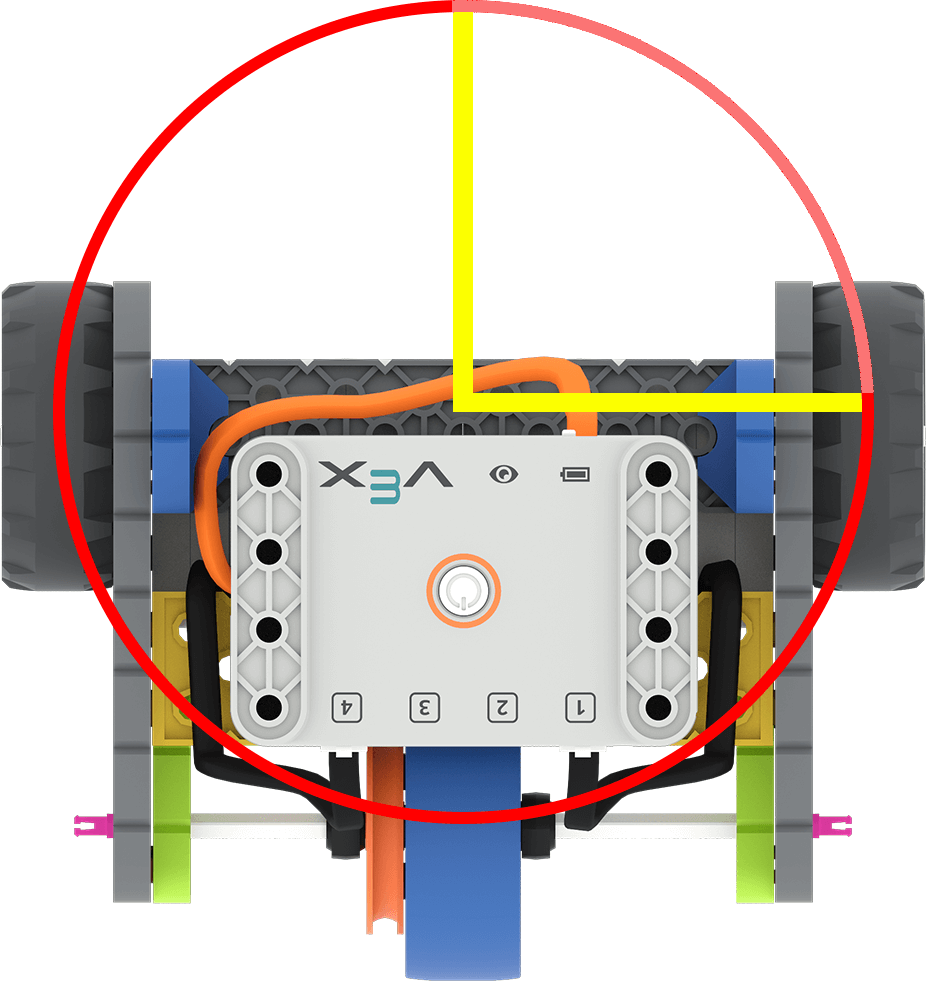
L'insegnante chiede alla classe cosa dovremmo inserire nel blocco [Gira per] per far girare il robot di 90°? Lo studente risponde “90”.	La distanza in gradi percorsa dalla ruota per sterzare è uguale all'angolo di sterzata. Gli studenti non utilizzano la circonferenza di sterzata del robot per calcolare la distanza in gradi che la ruota deve percorrere.	Ricordare agli studenti che affinché il robot possa girare, le ruote devono muoversi lungo la circonferenza di svolta. (In questa immagine, si tratta del cerchio rosso, da una linea gialla all'altra.) Girare la ruota di soli 90° per aiutare gli studenti a visualizzare la distanza percorsa dalla ruota per percorrere una determinata distanza.
L'insegnante chiede alla classe cosa dovremmo inserire nel blocco [Gira per] per far avanzare il robot di 12 pollici? Lo studente risponde “12”.	Il numero di giri della ruota è pari alla distanza di percorrenza desiderata. Lo studente non utilizza la circonferenza della ruota per calcolare il numero di giri della ruota necessari per percorrere la distanza desiderata.	Ricordare agli studenti di quanto si muove il robot con un giro di ruota e chiedere se 12 giri completi sembrano troppi o troppo pochi per percorrere 12 pollici. Per aiutare gli studenti a visualizzarlo meglio, fate girare una ruota lungo un righello per 12 giri, per mostrare loro quanto è lunga quella distanza. Ricorda agli studenti che 1 giro di ruota è la circonferenza della ruota e che 12 pollici devono essere divisi per quella circonferenza.
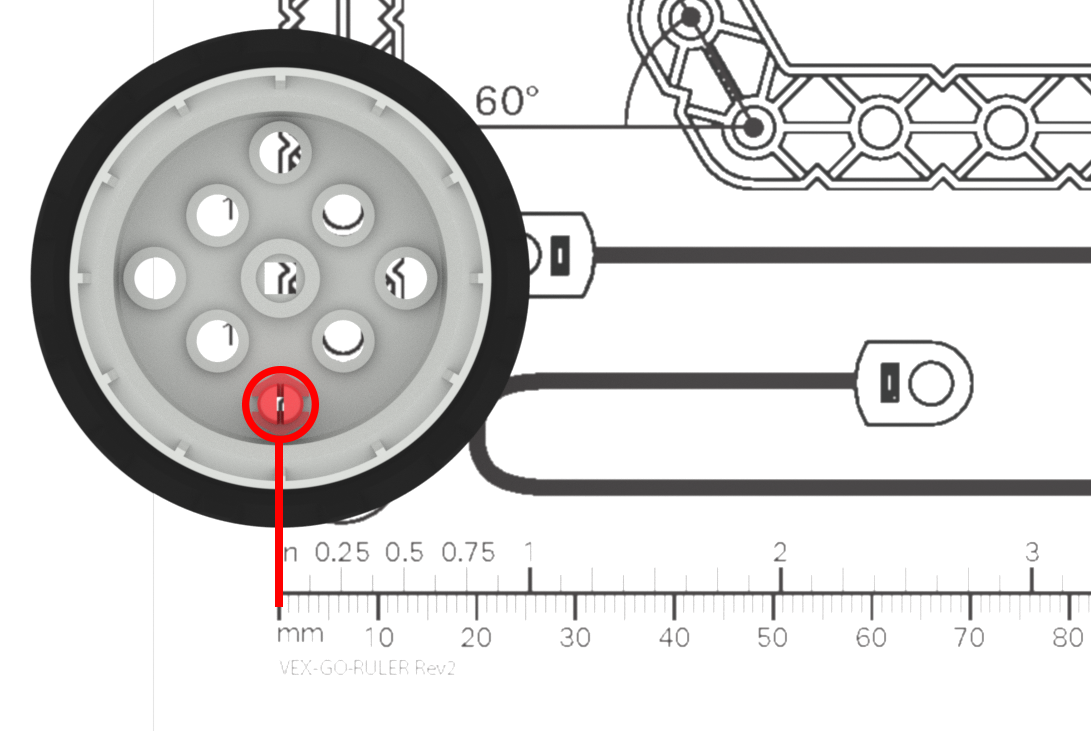
Lo studente sta misurando la ruota, ma nessuno dei due bordi della ruota è sul segno zero del righello	Il righello inizia da 1, non da zero. Lo studente non utilizza correttamente il righello per ottenere una misurazione accurata.	Ricordare agli studenti che il righello inizia dal segno "0" e che se non misurano da quel punto, le loro misurazioni saranno errate. Per fornire agli studenti un ulteriore ausilio visivo durante il lavoro, è possibile contrassegnare l'inizio del righello con del nastro adesivo o un pennarello colorato. (Per extra pratica con la misurazione, gli studenti possono completare il Pratica Attività di misurazione.)
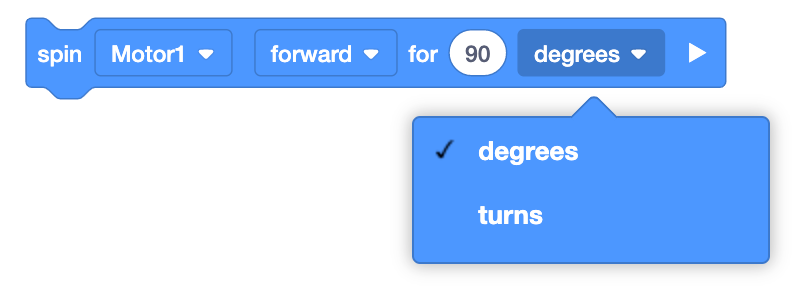
Uno studente dice che il suo progetto non funziona. L'insegnante nota che il numero corretto di giri della ruota è nel blocco [Gira per], ma il parametro è impostato su "gradi".	Le unità o i parametri sono intercambiabili. Gli studenti non prestano attenzione ai parametri/unità di misura nel loro progetto.	Chiedere agli studenti quale unità di misura stanno utilizzando e se questa corrisponde al parametro nel blocco. Ricordare agli studenti che i loro calcoli funzioneranno come previsto solo se il parametro è impostato sull'unità corretta. Giri e gradi non hanno lo stesso valore.
Uno studente prova a immettere '21/4' nel parametro del blocco [Spin for], per immettere "2 ¼ giri".	Le frazioni e i numeri decimali si scrivono nello stesso modo. Lo studente non sta convertendo la frazione in un numero decimale.	Ricordare agli studenti che devono convertire le frazioni in decimali affinché siano parametri riconoscibili. Per fare ciò, dividi il numeratore per il denominatore. 2 ¼=94 =2,25 Potresti chiedere agli studenti di rappresentare graficamente i valori frazionari usati di frequente e i loro equivalenti decimali per creare le proprie risorse.
L'insegnante chiede agli studenti di condividere il calcolo della circonferenza della ruota. Risposte degli studenti ~ 83,2 mm.	La circonferenza viene calcolata utilizzando il raggio -πxraggio. Lo studente utilizza la misura sbagliata nel calcolo.	Remind students that the circumference is π x diameter; and the diameter is a straight line across the center of the wheel (or twice the radius).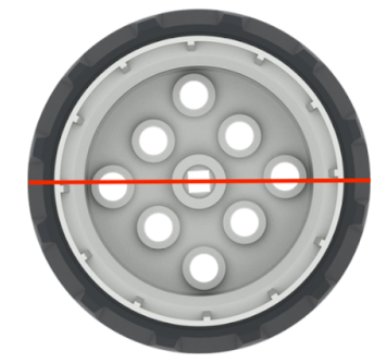 Potresti voler misurare e calcolare il valore come attività dell'intera classe se molti studenti hanno difficoltà con l'uso delle formule.

Situazione

Idea sbagliata

Correzione suggerita

L'insegnante chiede alla classe cosa dovremmo inserire nel blocco [Gira per] per far girare il robot di 90°?

Lo studente risponde “90”.

La distanza in gradi percorsa dalla ruota per sterzare è uguale all'angolo di sterzata.

Gli studenti non utilizzano la circonferenza di sterzata del robot per calcolare la distanza in gradi che la ruota deve percorrere.

Ricordare agli studenti che affinché il robot possa girare, le ruote devono muoversi lungo la circonferenza di svolta. (In questa immagine, si tratta del cerchio rosso, da una linea gialla all'altra.)

Immagine dall'alto del Code Base con il cerchio in alto che indica la circonferenza. Le linee gialle a ore 12 e a ore 3 delimitano i 90 gradi dell'intero cerchio.

Girare la ruota di soli 90° per aiutare gli studenti a visualizzare la distanza percorsa dalla ruota per percorrere una determinata distanza.

L'insegnante chiede alla classe cosa dovremmo inserire nel blocco [Gira per] per far avanzare il robot di 12 pollici?

Lo studente risponde “12”.

Il numero di giri della ruota è pari alla distanza di percorrenza desiderata.

Lo studente non utilizza la circonferenza della ruota per calcolare il numero di giri della ruota necessari per percorrere la distanza desiderata.

Ricordare agli studenti di quanto si muove il robot con un giro di ruota e chiedere se 12 giri completi sembrano troppi o troppo pochi per percorrere 12 pollici.

Per aiutare gli studenti a visualizzarlo meglio, fate girare una ruota lungo un righello per 12 giri, per mostrare loro quanto è lunga quella distanza.

Uno schema mostra una ruota VEX GO con un perno rosso nel mozzo sopra il righello stampabile. Il perno è allineato con il segno 0 mm del righello VEX GO, mostrando come contrassegnare con precisione la sterzata di una ruota.

Ricorda agli studenti che 1 giro di ruota è la circonferenza della ruota e che 12 pollici devono essere divisi per quella circonferenza.

Lo studente sta misurando la ruota, ma nessuno dei due bordi della ruota è sul segno zero del righello

Il righello inizia da 1, non da zero.

Lo studente non utilizza correttamente il righello per ottenere una misurazione accurata.

Ricordare agli studenti che il righello inizia dal segno "0" e che se non misurano da quel punto, le loro misurazioni saranno errate.

Per fornire agli studenti un ulteriore ausilio visivo durante il lavoro, è possibile contrassegnare l'inizio del righello con del nastro adesivo o un pennarello colorato. (Per extra pratica con la misurazione, gli studenti possono completare il Pratica Attività di misurazione.)

Uno studente dice che il suo progetto non funziona.

L'insegnante nota che il numero corretto di giri della ruota è nel blocco [Gira per], ma il parametro è impostato su "gradi".

Le unità o i parametri sono intercambiabili.

Gli studenti non prestano attenzione ai parametri/unità di misura nel loro progetto.

Chiedere agli studenti quale unità di misura stanno utilizzando e se questa corrisponde al parametro nel blocco.

Un blocco VEXcode GO Spin con il menu a discesa dei parametri dell'unità aperto e i gradi selezionati. Il blocco riporta Spin Motor1 in avanti di 90 gradi. Ricordare agli studenti che i loro calcoli funzioneranno come previsto solo se il parametro è impostato sull'unità corretta. Giri e gradi non hanno lo stesso valore.

Uno studente prova a immettere '21/4' nel parametro del blocco [Spin for], per immettere "2 ¼ giri".

Le frazioni e i numeri decimali si scrivono nello stesso modo.

Lo studente non sta convertendo la frazione in un numero decimale.

Ricordare agli studenti che devono convertire le frazioni in decimali affinché siano parametri riconoscibili. Per fare ciò, dividi il numeratore per il denominatore.
2 ¼=94 =2,25
Potresti chiedere agli studenti di rappresentare graficamente i valori frazionari usati di frequente e i loro equivalenti decimali per creare le proprie risorse.

L'insegnante chiede agli studenti di condividere il calcolo della circonferenza della ruota.

Risposte degli studenti
~ 83,2 mm.

La circonferenza viene calcolata utilizzando il raggio -πxraggio.

Lo studente utilizza la misura sbagliata nel calcolo.

Remind students that the circumference is π x diameter; and the diameter is a straight line across the center of the wheel (or twice the radius).
A top down diagram of the VEX GO Wheel with a red line across the center indicating the diameter of the wheel.

A top down diagram of the VEX GO Wheel with a red line across the center indicating the diameter of the wheel.

Potresti voler misurare e calcolare il valore come attività dell'intera classe se molti studenti hanno difficoltà con l'uso delle formule.

Soluzioni di esempio

Lab 4 Esempio di soluzione

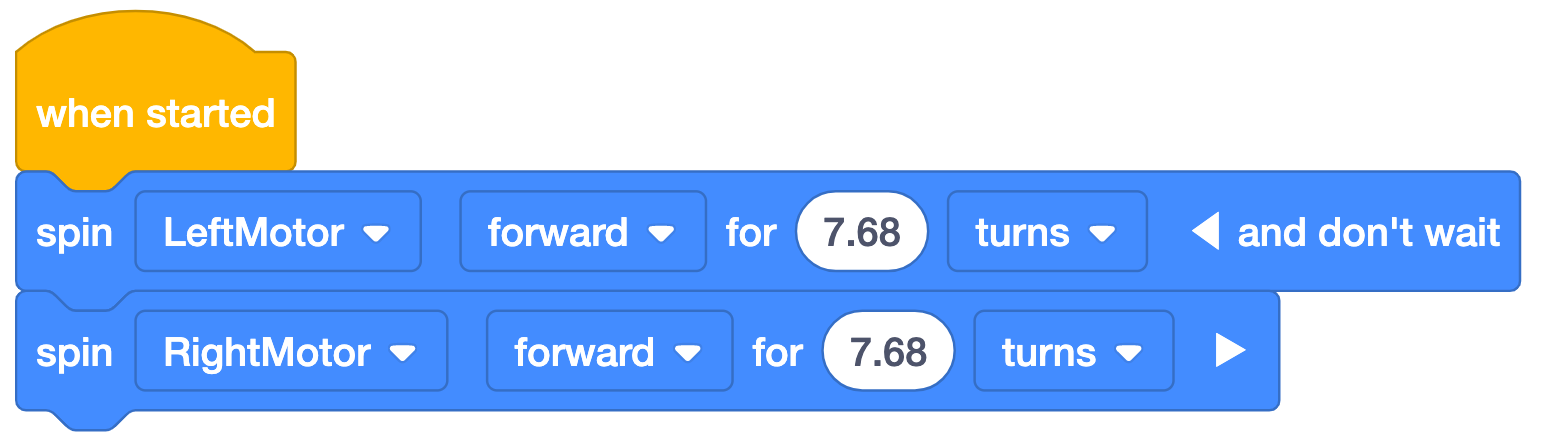
*Nota: "e non aspettare" viene utilizzato con il primo blocco nel progetto di esempio in modo che entrambi i blocchi vengano eseguiti simultaneamente. Senza "e non aspettare", il primo motore girerebbe, poi il secondo e la base di codice non funzionerebbe come previsto. Assicuratevi che gli studenti NON nascondano la dicitura "e non aspettare", altrimenti il loro progetto non verrà eseguito come previsto.

Percorso della parata costituito da 5 tessere VEX GO collegate in linea orizzontale. Ci sono delle linee rosse in corrispondenza della prima e dell'ultima linea nera verticale sulle Tile, che indicano l'inizio e la fine a 48 pollici di distanza. Il codice base è mostrato nella posizione iniziale con le ruote allineate sulla linea rossa all'estrema destra.

Per percorrere i 48 pollici (~122 cm) del percorso della parata, il Code Base dovrà percorrere ~7,68 curve. Il calcolo è mostrato a sinistra, mentre l'esempio della soluzione VEXcode GO è mostrato a destra.
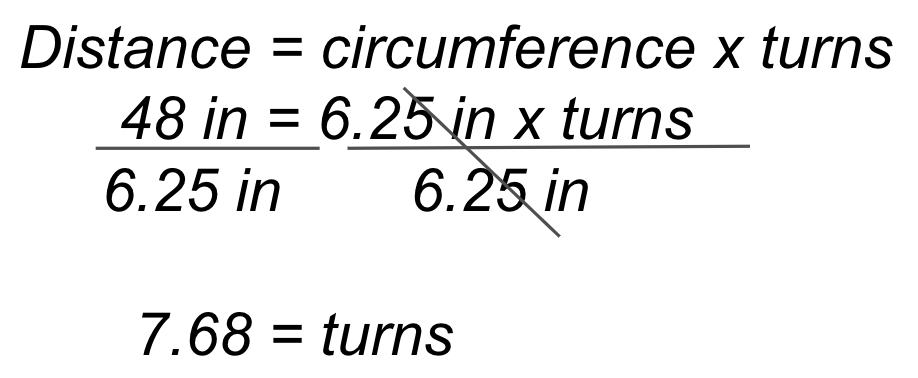
Una soluzione di esempio recita: Distanza uguale Circonferenza moltiplicata per giri della ruota, con i valori sottostanti che indicano 48 pollici = 6,25 pollici moltiplicati per giri. Entrambi i lati dell'equazione vengono divisi per 6,25 pollici, ottenendo così 7,68 giri uguali. Un progetto VEXcode GO inizia con un blocco When started e ha due blocchi Spin for allegati. I blocchi riportano la scritta "Una volta avviato, far girare il motore sinistro in avanti per 7,68 giri e non aspettare; quindi far girare il motore destro in avanti per 7,68 giri".

Lab 5 Esempio di soluzione

Per percorrere i 48 pollici (~122 cm) di lunghezza del percorso della parata e girare di 180 gradi, il Code Base dovrà procedere in avanti per ~7,68 svolte, quindi girare un motore in avanti e l'altro indietro per ~1,47 svolte. Il calcolo è mostrato accanto all'esempio di soluzione VEXcode GO sulla destra.

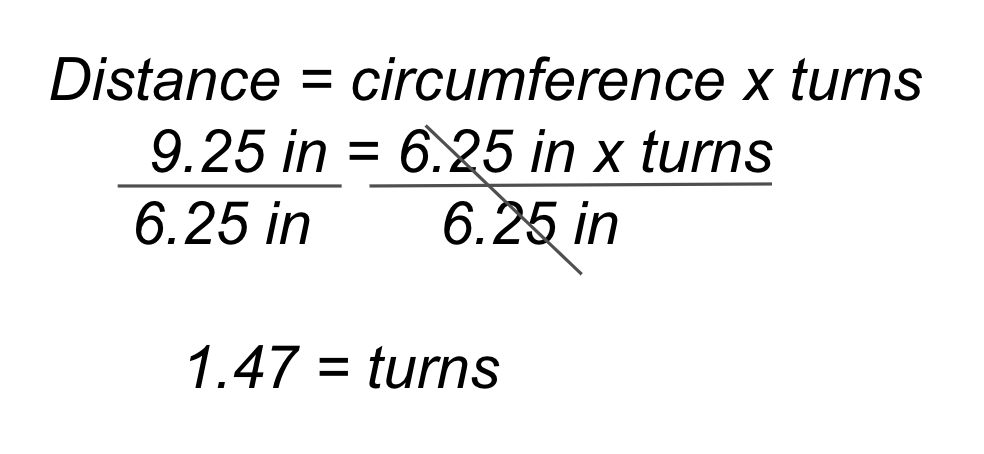
Una soluzione di esempio recita: Distanza uguale Circonferenza moltiplicata per giri della ruota, con i valori sottostanti che indicano 9,25 pollici = 6,25 pollici moltiplicati per giri. Entrambi i lati dell'equazione vengono divisi per 6,25 pollici, ottenendo così 1,47 giri uguali.

Nota: per usare i gradi invece delle svolte, moltiplicare per 360.

Estensione percorso sfilata

Se gli studenti hanno bisogno di una sfida in più, è possibile estendere il percorso della parata in molti modi diversi. Questo è un esempio, con una possibile soluzione.

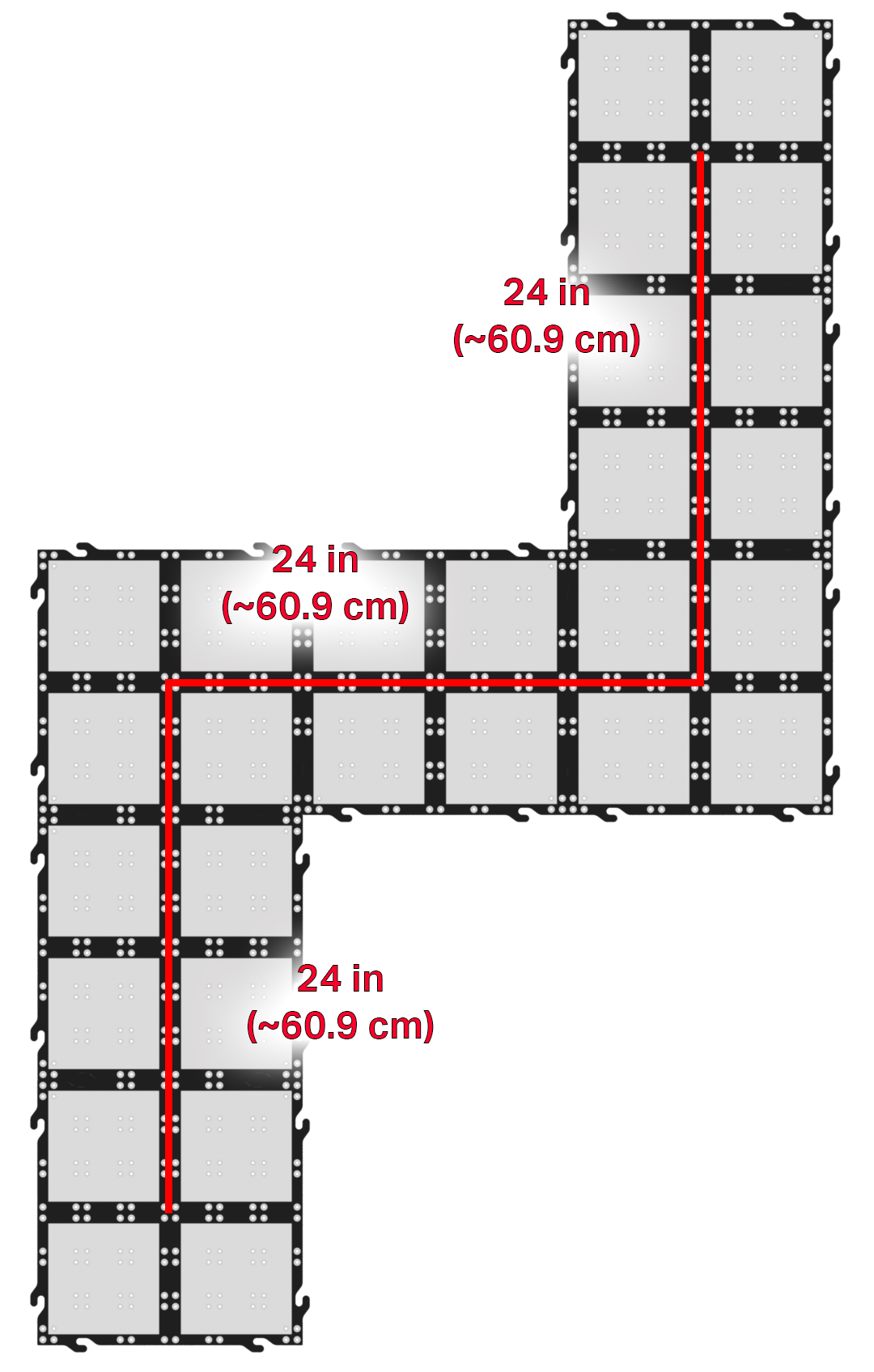
Uno schema dell'estensione del percorso della parata che mostra le 7 tessere VEX GO collegate per formare un percorso che si sviluppa verticalmente per 24 pollici, gira a destra e si estende orizzontalmente per 24 pollici, quindi gira a sinistra e si estende verticalmente per 24 pollici. — Esempio di possibile estensione del percorso della parata

In questo percorso di esempio, le distanze di guida e le svolte sono dimezzate rispetto ai Labs. In questo percorso, tuttavia, la direzione delle svolte è importante. Oltre a ricalcolare, gli studenti dovranno capire in che direzione far girare le ruote per girare nella direzione desiderata.
I calcoli dimezzati dei laboratori precedenti sono i seguenti:

Distanza di guida = ~ 3,84 svolte
Distanza di svolta = ~ 0,73 svolte

Questi valori vengono utilizzati nel seguente esempio di soluzione VEXcode GO:

< Indietro Ritorna ai laboratori Seguente >