Apoyo matemático
Al enseñar los laboratorios 4 y 5, se involucran conceptos y cálculos matemáticos adicionales. Esta página ofrece a los docentes recursos de fondo relevantes para apoyar las matemáticas que los estudiantes están explorando en estos laboratorios.
Matemáticas de la conducción
Para completar el desfile en el Laboratorio 4, los estudiantes conducirán su carroza Code Base a lo largo
de una ruta de desfile recta. En lugar de utilizar bloques de transmisión que mueven ambas ruedas al mismo
tiempo, los estudiantes usarán los bloques [Girar para] en VEXcode GO, como se muestra aquí, para girar los
motores conectados a las ruedas y mover el robot hacia adelante. Los bloques [Girar para] aceptan 'giros' o
'grados' como parámetros. En el Laboratorio 4, los estudiantes calcularán la cantidad de vueltas que deberán
ingresar en este proyecto para conducir su robot a lo largo de la ruta del desfile.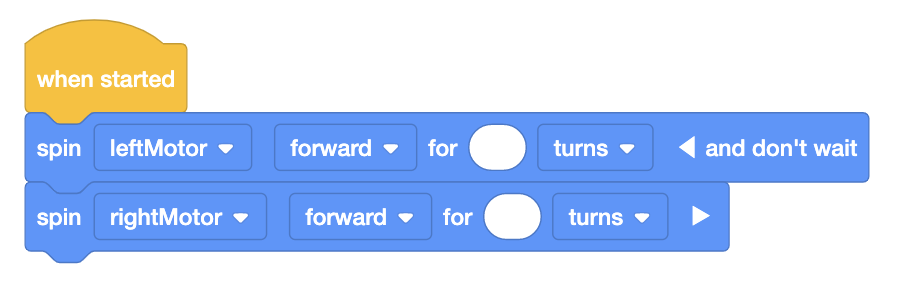
Mire el video a continuación para aprender a calcular la cantidad de vueltas de rueda necesarias para conducir su robot en línea recta durante una distancia determinada.
Referencias útiles:
Terminología y valores de las ruedas grises:
| Término | Definición | Visual | Fórmula | Valor |
|---|---|---|---|---|
| Diámetro | Medición de una línea recta a través del centro de un círculo. | 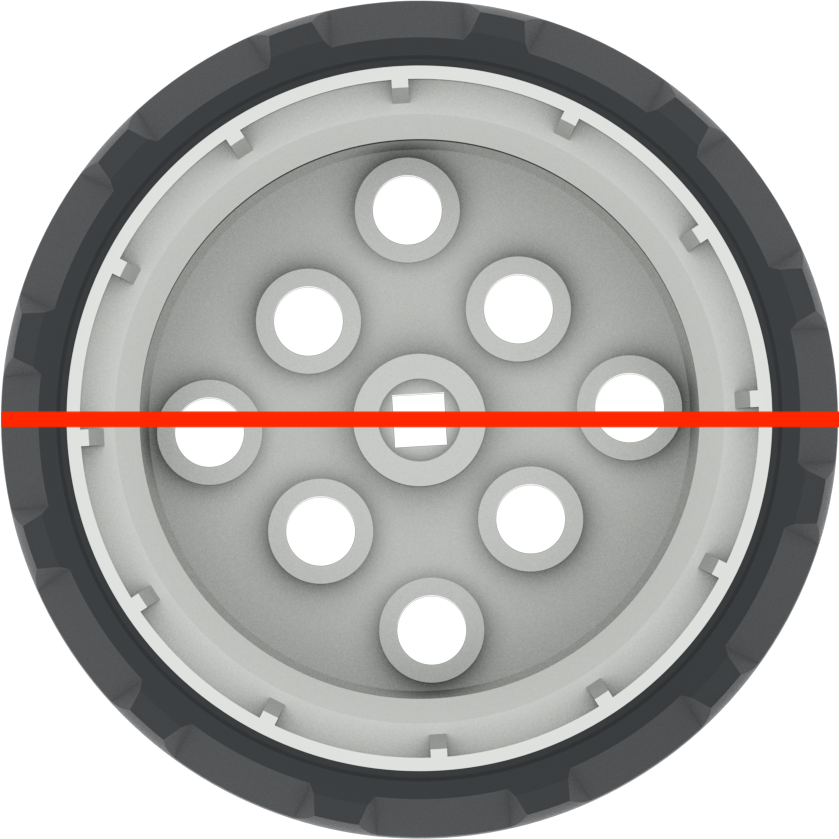 |
d = 2r | ~ 50,93 mm o 2 pulgadas |
| Circunferencia | La distancia total alrededor del exterior de un círculo. |  |
C = πd | ~ 160 mm o 6,25 pulgadas |
Medición precisa
Cuando los estudiantes estén midiendo, asegúrese de guiarlos para que midan con cuidado y precisión. puedes usarla regla imprimible VEX GOpara que los estudiantes midan, o reglas de aula.
- Recuerde a los estudiantes que deben comenzar a medir desde el punto cero de la regla, y prestar mucha atención al punto final del objeto que están midiendo. Comenzar o finalizar sus mediciones de manera incorrecta afectará sus cálculos y el movimiento final de su robot.
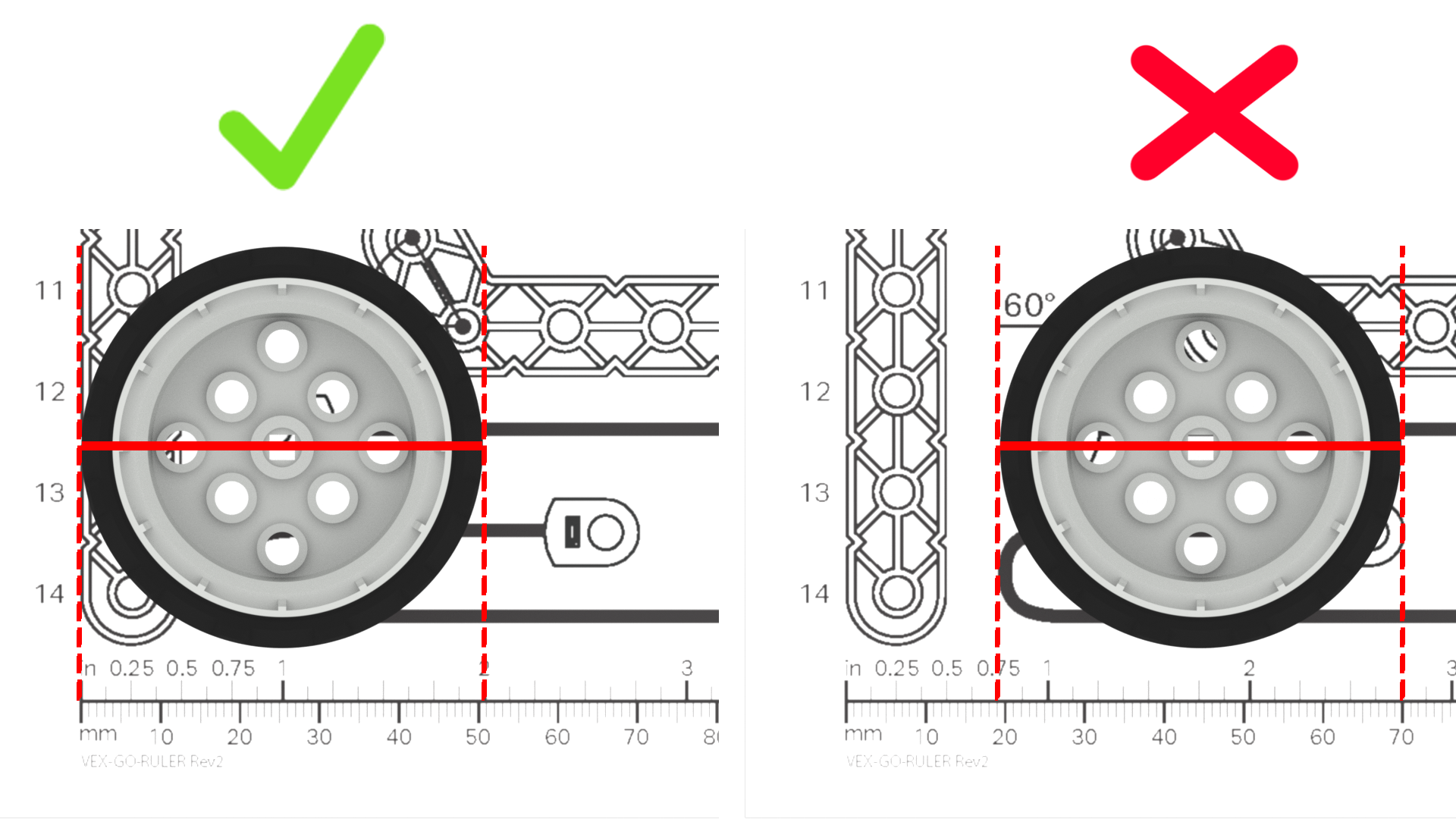
- Asegúrese de que los estudiantes sepan cómo leer las marcas en la regla que están usando, para poder medir con precisión. Si las reglas que estás usando tienen unidades imperiales y métricas (como la regla imprimible VEX GO) asegúrese de que los estudiantes utilicen consistentemente las mismas unidades de medida.
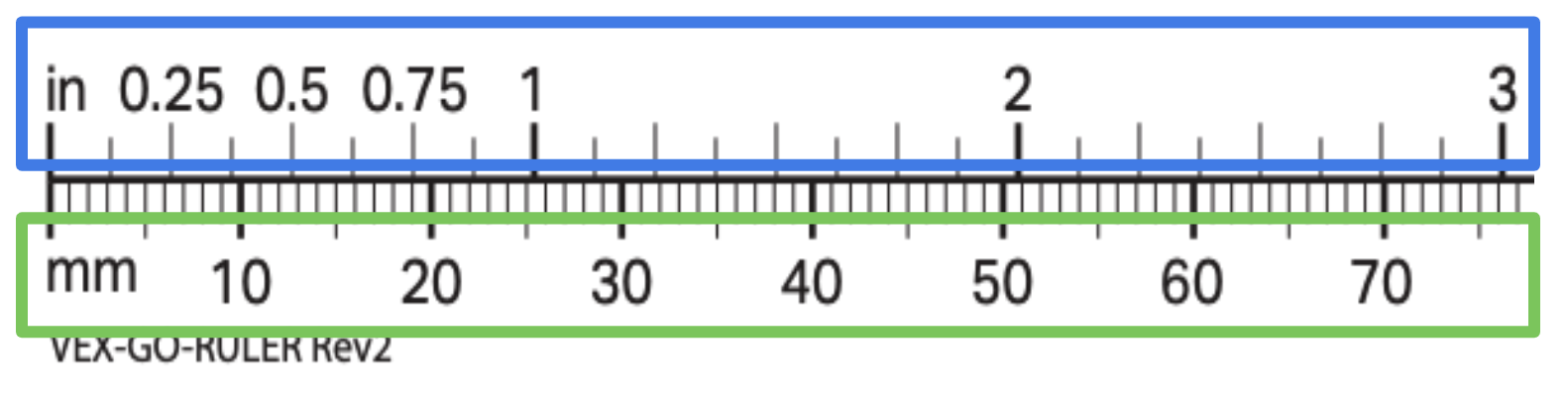
- Los estudiantes pueden redondear sus medidas a la unidad más cercana, o fracción de una unidad. El redondeo puede hacer que los cálculos sean más sencillos, si es necesario, pero también puede hacer que las mediciones sean menos precisas. Por ejemplo, puede indicar a los estudiantes que redondeen a la media pulgada o centímetro más cercano, pero su robot se mueve un poco más lejos de lo previsto inicialmente. Como alternativa, puede pedir a los estudiantes que midan hasta el ⅛ de pulgada o milímetro más cercano y descubran que sus robots se desplazan más cerca de la distancia prevista.
- If students need extra practice with measuring, puedes usar el Práctica Medición de la actividad VEX GOcon estudiantes individuales o grupos, o como una actividad de toda la clase.
Matemáticas del giro de 360°
Para completar el desfile en el Laboratorio 5, los estudiantes conducirán su carroza Code Base a lo largo de una ruta de desfile con un giro.
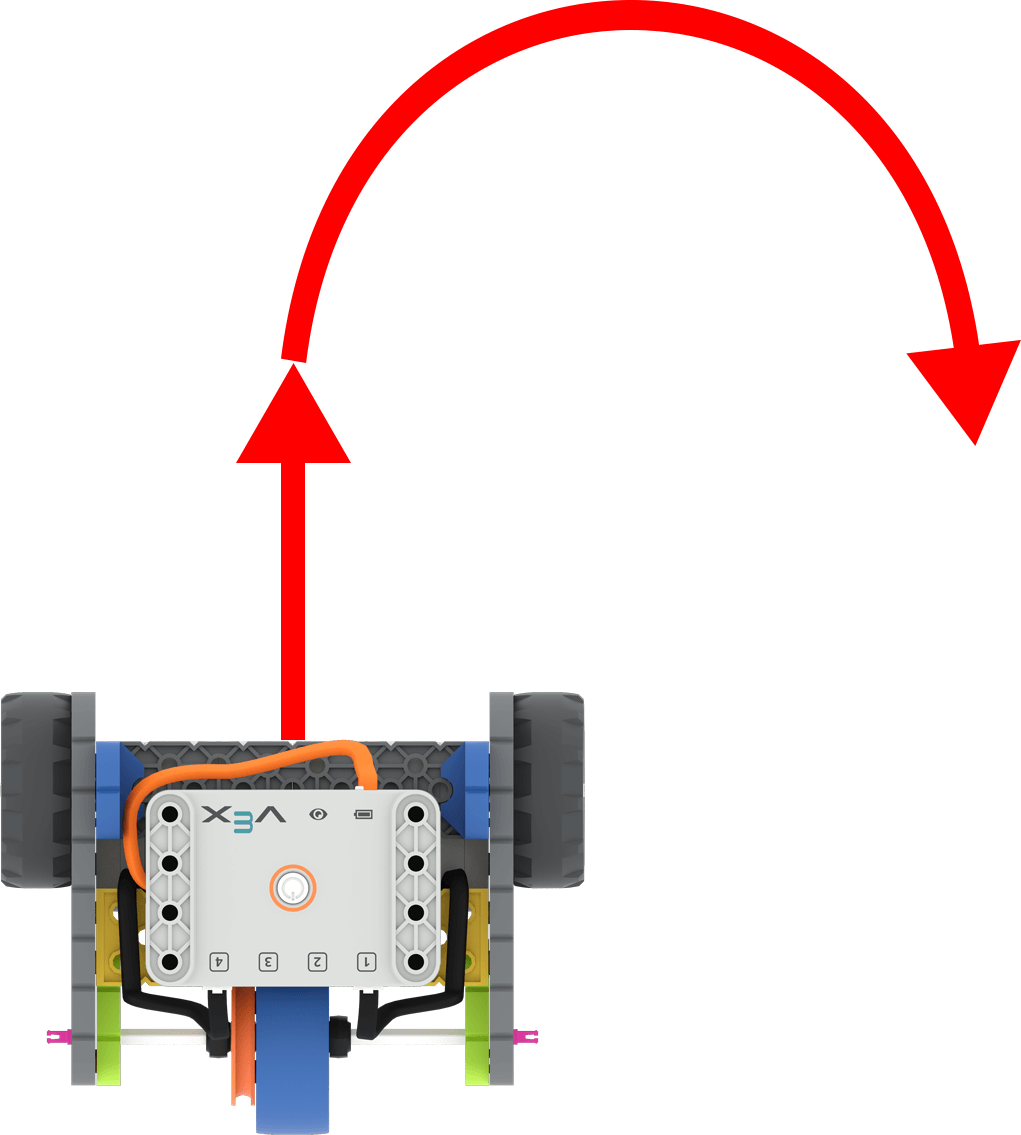
Código base con flechas para mostrar cómo se conduce hacia adelante y luego se gira a la derecha
Los estudiantes se basarán en lo que aprendieron sobre cómo codificar el robot para recorrer una distancia
en línea recta, para codificar el robot para conducir una distancia no lineal o un giro. Los estudiantes
todavía están calculando la cantidad de vueltas necesarias para recorrer una distancia determinada, por lo
que utilizarán la misma fórmula que en el laboratorio anterior.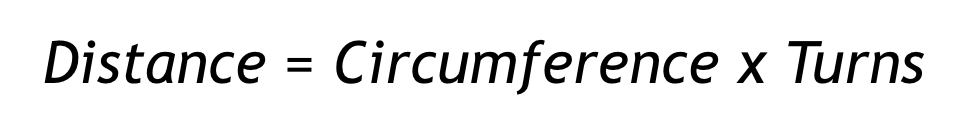
Mira el video a continuación para aprender a calcular la cantidad de vueltas de rueda necesarias para realizar un giro de del robot con tus estudiantes.
Referencias útiles:
Cuando la base del código gira, las ruedas motrices se mueven en direcciones opuestas para girar el robot. Por ejemplo, para girar el robot hacia la derecha, la rueda izquierda se moverá hacia adelante, mientras que la rueda derecha se moverá hacia atrás.
Terminología y valores para la base de código:
| Término | Definición | Visual | Fórmula | Valor |
|---|---|---|---|---|
| Diámetro | Medición de una línea recta desde el centro de cada rueda (también conocida como distancia entre ejes) |  |
d = 2r | ~ 135 mm o 5,3 pulgadas |
| Circunferencia | La distancia total recorrida por las ruedas para completar un giro de 360°. | 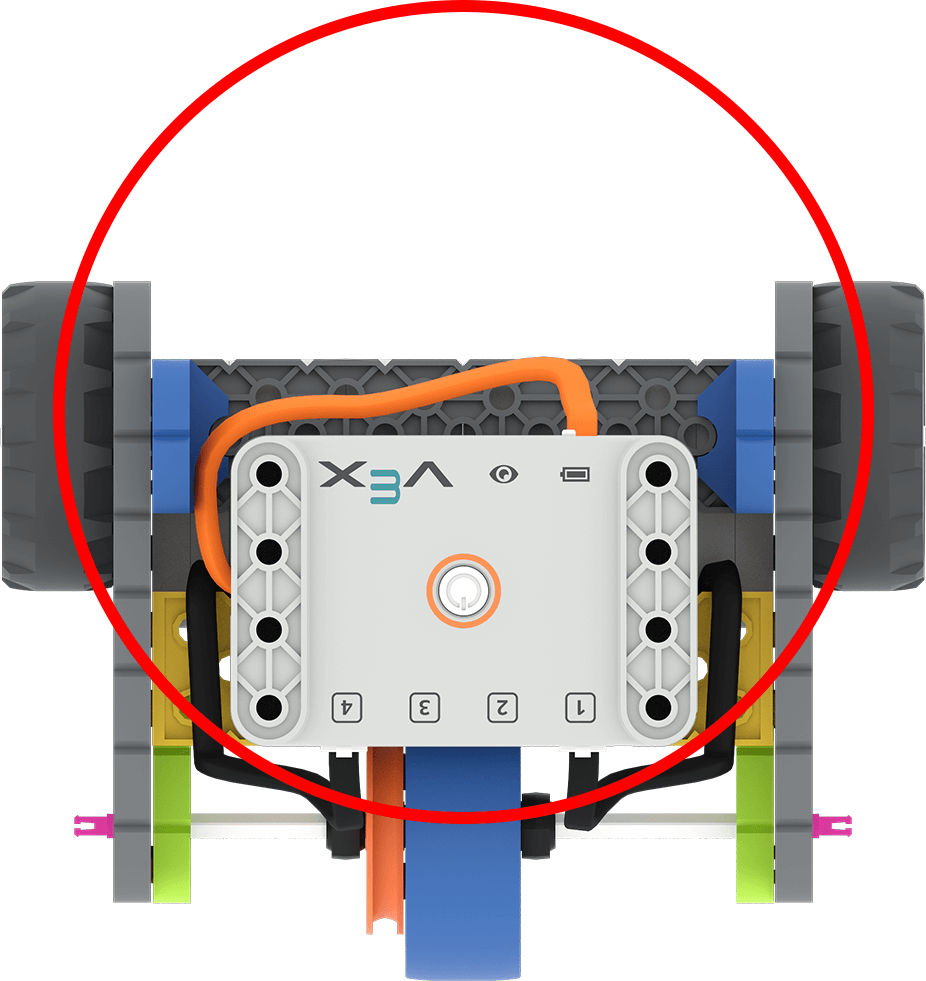
|
C = πd | ~ 424 mm o 16,7 pulgadas |
Matemáticas para girar cualquier grado
Mire este video para obtener más información sobre cómo calcular la cantidad de vueltas de rueda necesarias para que el robot gire cualquier grado.
Conversión a grados
El bloque [Girar para] aceptará giros o grados como parámetros.
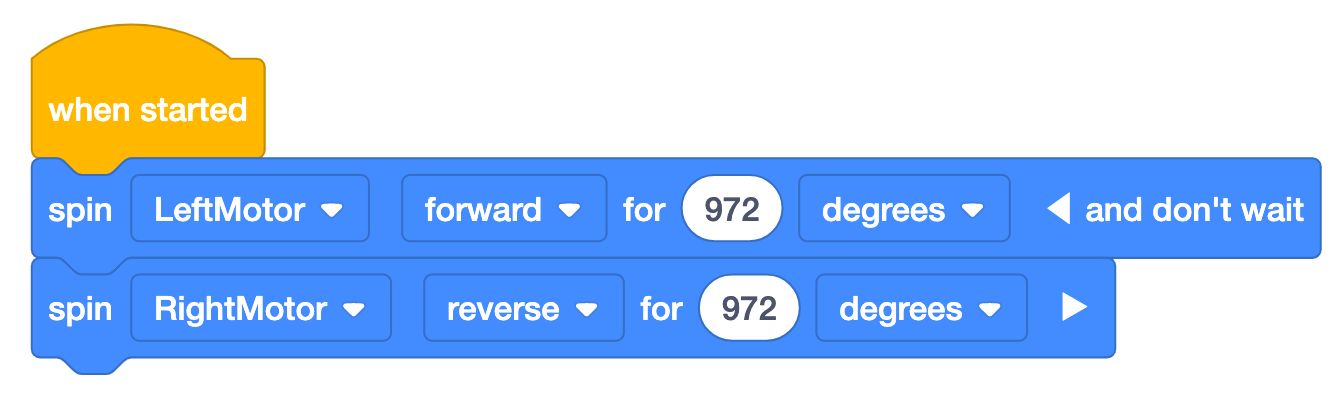
Para utilizar grados, simplemente multiplique el número de vueltas por 360. Este ejemplo muestra la cantidad
de grados que girarán los motores para rotar el robot° completos. Tenga en cuenta que en este
proyecto los motores giran en direcciones opuestas y se agrega "y no espere" al primer bloque, por lo que
los motores giran simultáneamente. Esto rotará el robot hacia la derecha hasta alcanzar los 360° deseados.
Conceptos erróneos comunes
Hay varios conceptos erróneos que los estudiantes pueden tener sobre la medición y las matemáticas de la conducción y los giros. Estas son algunas de las más comunes, con sugerencias sobre cómo abordarlas con sus estudiantes.
| Situación | Idea falsa | Corrección sugerida |
|---|---|---|
|
El profesor pregunta a la clase: ¿qué debemos ingresar en el bloque [Girar para] para que el robot gire 90°? El estudiante responde “90”. |
La distancia en grados que recorre la rueda para realizar un giro es igual al ángulo de giro. Los estudiantes no utilizan la circunferencia de giro del robot para calcular la distancia en grados que debe recorrer la rueda. |
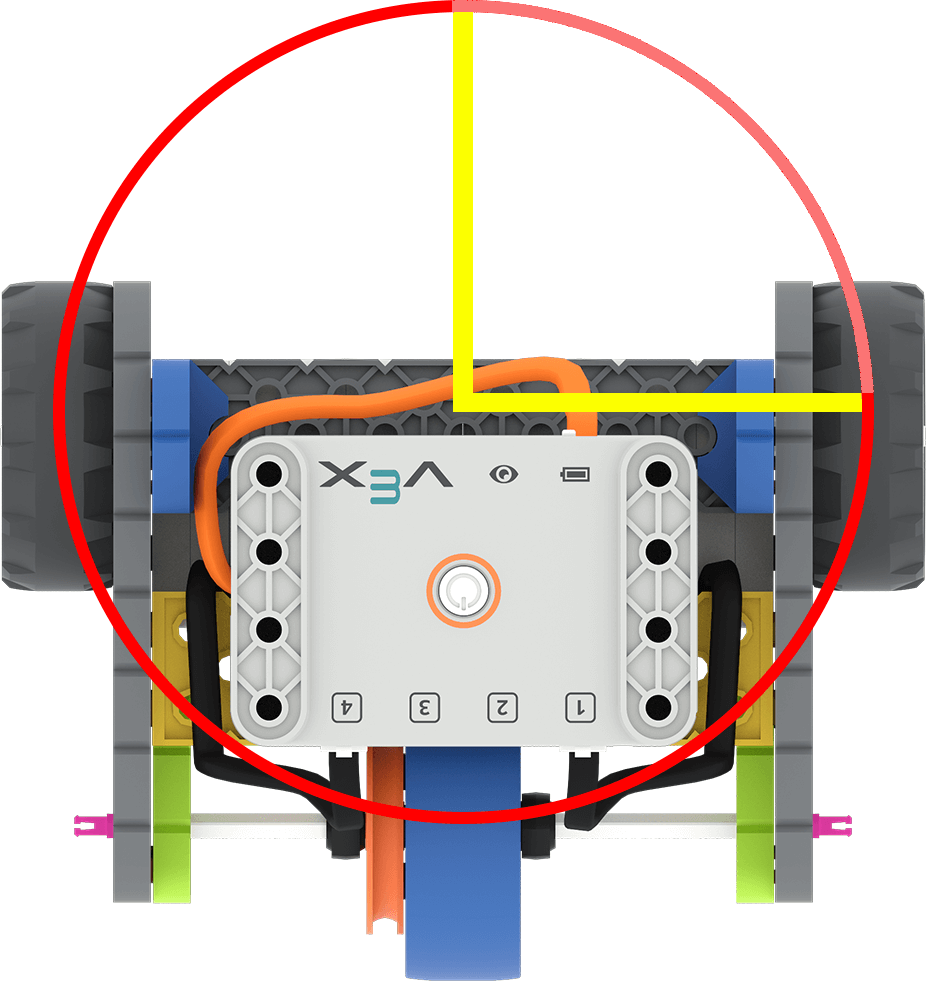
Recuerde a los estudiantes que las ruedas deben moverse a lo largo de la circunferencia de giro para que el robot gire. (En esta imagen, esto es a lo largo del círculo rojo desde una línea amarilla a la otra).
Gire la rueda solo 90° para ayudar a los estudiantes a visualizar cuánto gira la rueda para recorrer una distancia determinada. |
|
El profesor pregunta a la clase: ¿qué debemos ingresar en el bloque [Girar para] para que el robot avance 12 pulgadas? El estudiante responde “12”. |
El número de vueltas de la rueda es igual a la distancia de conducción deseada. El estudiante no está utilizando la circunferencia de la rueda para calcular el número de vueltas de la rueda para recorrer la distancia deseada. |
Recuerde a los estudiantes qué tan lejos se mueve el robot con un giro de rueda y pregúnteles si 12 parecen demasiadas o muy pocas vueltas completas para recorrer 12 pulgadas. Para ayudar a los estudiantes a visualizar esto mejor, haga rodar una rueda a lo largo de una regla durante 12 vueltas, para mostrarles qué tan grande es esa distancia.
Recuerde a los estudiantes que 1 vuelta de rueda es la circunferencia de la rueda y que 12 pulgadas deben dividirse por esa circunferencia. |
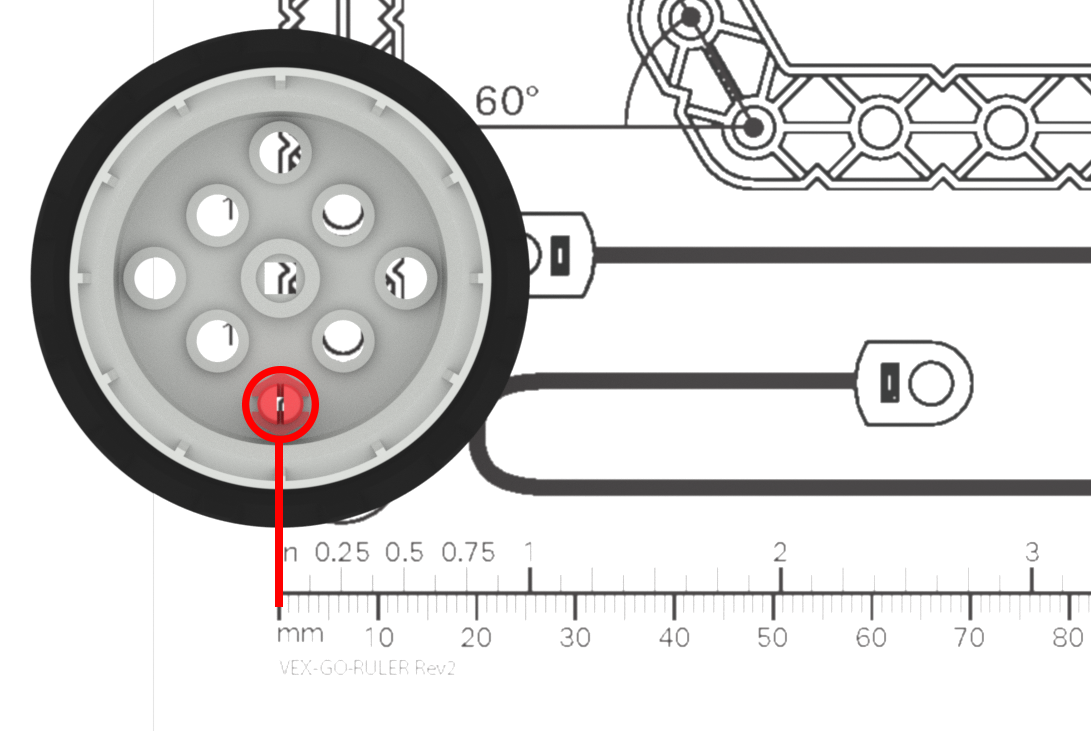
| El estudiante está midiendo la rueda, pero los bordes de la rueda está en la marca cero de la regla. |
La regla comienza en 1, no en cero. El estudiante no está utilizando la regla correctamente para obtener una medida precisa. |
Recuerde a los estudiantes que la regla comienza en la marca "0" y que si no miden desde ese punto, sus medidas serán incorrectas. Es posible que desees marcar el inicio de la regla con cinta o un marcador de color, como ayuda visual adicional para los estudiantes mientras trabajan. (For extra practice with measuring, students can complete the Practice Measuring Activity.) |
|
Un estudiante dice que su proyecto no está funcionando. El profesor observa que el número correcto de vueltas de rueda está en el bloque [Girar durante], pero el parámetro está establecido en "grados". |
Las unidades o parámetros son intercambiables. Los estudiantes no están prestando atención a los parámetros/unidades de medida en su proyecto. |
Pregunte a los estudiantes qué unidad de medida están usando y si coincide con el parámetro en el bloque.
|
| Un estudiante intenta ingresar '21/4' en el parámetro del bloque [Girar para], para ingresar “2 ¼ vueltas”. |
Las fracciones y los decimales se escriben de la misma manera. El estudiante no está convirtiendo la fracción a decimal. |
Recuerde a los estudiantes que deben convertir fracciones a decimales para que sean parámetros
reconocibles. Para hacer esto, divida el numerador por el denominador. 2 ¼=94 =2,25 Es posible que desee pedir a los estudiantes que grafican los valores fraccionarios utilizados con frecuencia y sus equivalentes decimales para crear su propio recurso. |
|
El profesor pide a los estudiantes que compartan su cálculo de la circunferencia de la rueda. Respuestas de los estudiantes |
La circunferencia se calcula utilizando el radio -πxradio. El estudiante está utilizando la medida incorrecta en el cálculo. |
Remind students that the circumference is π x
diameter; and the diameter is a straight line across the center
of the wheel (or twice the radius).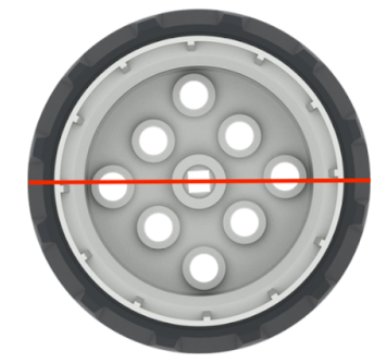 You may want to measure and calculate value as a whole class activity if many students are having difficulty with using the formulas. |
Ejemplos de soluciones
Solución de ejemplo de laboratorio 4
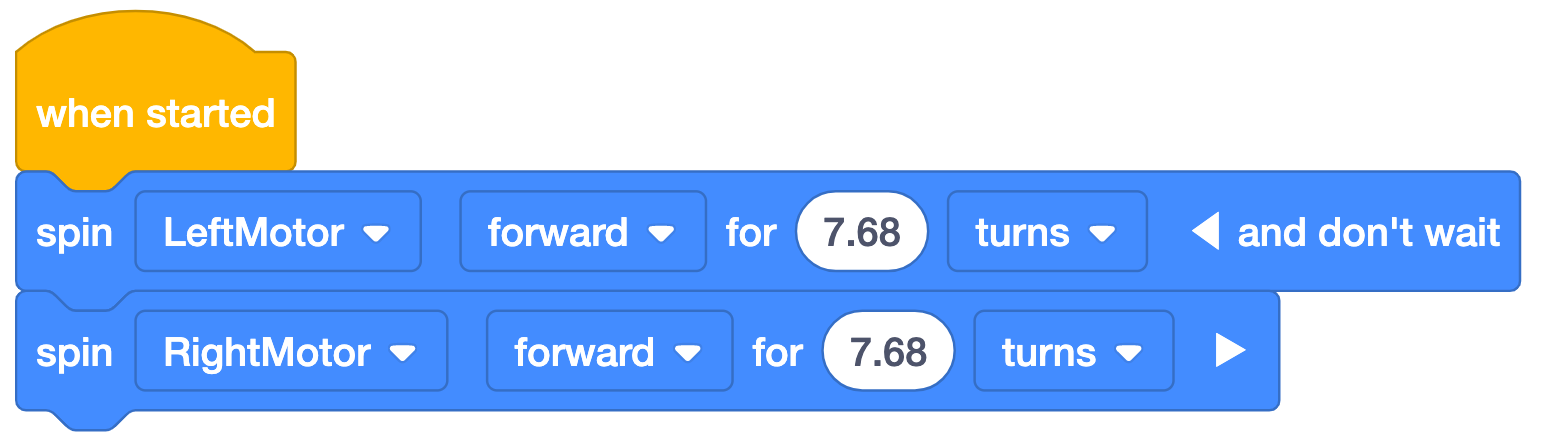
*Nota: Se utiliza 'y no esperar' con el primer bloque en el proyecto de ejemplo para que ambos bloques se ejecuten simultáneamente. Sin "y no esperes", el primer motor giraría, luego el segundo, y el Código Base no funcionaría como corresponde. Asegúrese de que los estudiantes NO colapsen el "y no esperen" o su proyecto no se ejecutará como se esperaba.

Para recorrer las 48 pulgadas (~122 cm) de longitud de la ruta del desfile, el Code Base deberá recorrer
y 7,68 vueltas. El cálculo se muestra a la izquierda y la solución de ejemplo VEXcode GO a
la derecha.
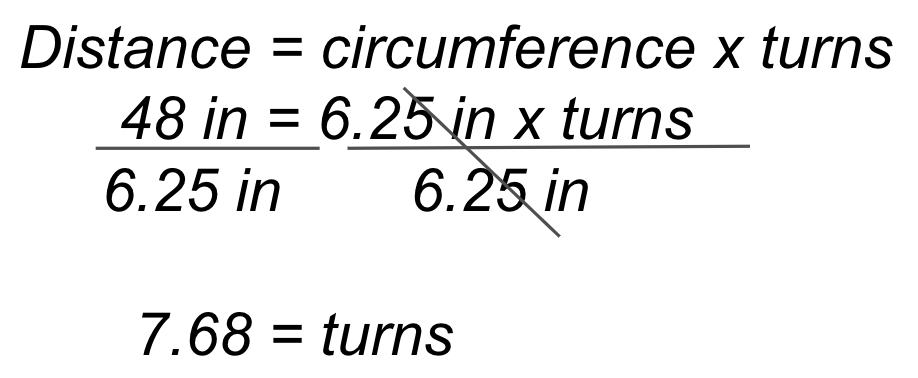
Solución de ejemplo de laboratorio 5
Para recorrer las 48 pulgadas (~122 cm) de longitud de la ruta del desfile y girar 180 grados, el Code Base deberá avanzar durante ~7,68 vueltas, luego girar un motor hacia adelante y el otro hacia atrás durante ~1,47 vueltas. El cálculo se muestra junto con el ejemplo de solución VEXcode GO a la derecha.
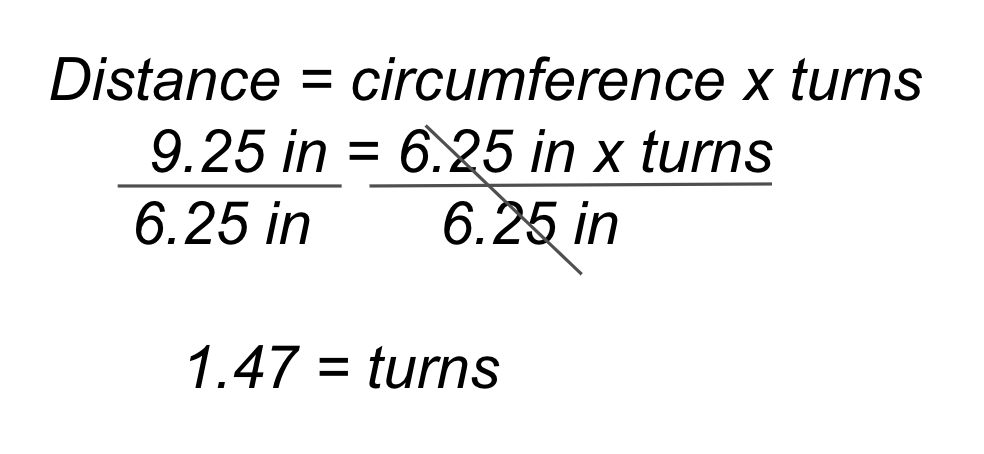

Nota: Para utilizar grados en lugar de vueltas, los cálculos de vueltas
por 360.
Ruta del desfile de extensión
Si los estudiantes necesitan un desafío adicional, puede ampliar la ruta del desfile de muchas maneras diferentes. Éste es un ejemplo, con una posible solución.
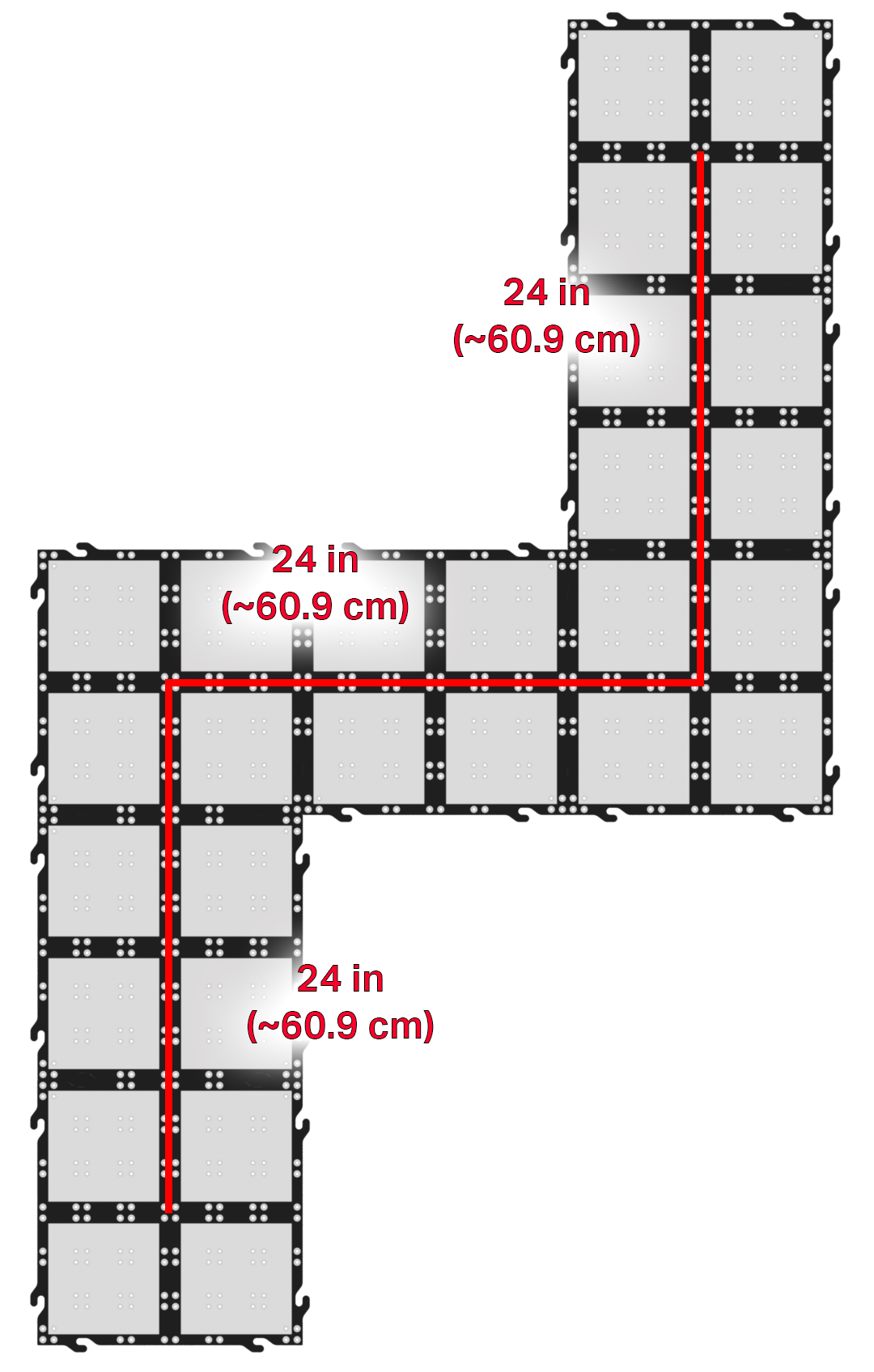
En esta ruta de ejemplo, las distancias de conducción y los giros se reducen a la mitad con respecto a los
de Labs. En esta ruta, sin embargo, la dirección de los giros importa. Además de volver a calcular, los
estudiantes tendrán que averiguar las direcciones para girar las ruedas para que giren en la dirección
deseada.
Los cálculos reducidos a la mitad de los laboratorios anteriores son los siguientes:
Distancia de conducción = ~ 3,84 vueltas
Distancia de giro = ~ 0,73
vueltas
Estos valores se utilizan en el siguiente ejemplo de solución VEXcode GO:
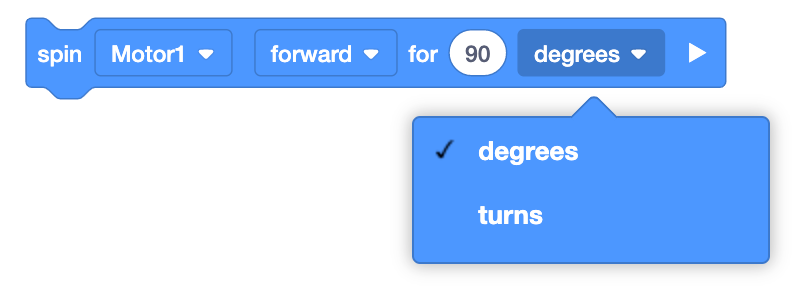 Recuerde a los estudiantes que sus cálculos solo funcionarán según lo
previsto si el parámetro está configurado en la unidad correcta. Los giros y los grados no tienen
el mismo valor.
Recuerde a los estudiantes que sus cálculos solo funcionarán según lo
previsto si el parámetro está configurado en la unidad correcta. Los giros y los grados no tienen
el mismo valor.