Soutien en mathématiques

Lors de l'enseignement des laboratoires 4 et 5, des concepts et des calculs mathématiques supplémentaires sont impliqués. Cette page offre aux enseignants des ressources de base pertinentes pour soutenir les mathématiques que les élèves explorent dans ces laboratoires.

Mathématiques de la conduite

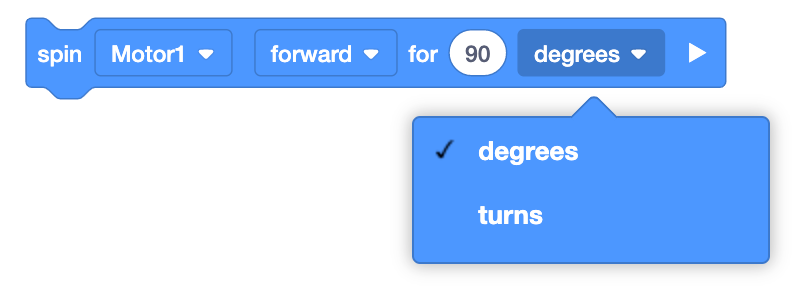
Pour terminer le défilé du laboratoire 4, les élèves conduiront leur char Code Base le long d'une distance de parcours de défilé en ligne droite. Au lieu d'utiliser des blocs de transmission qui déplacent les deux roues en même temps, les élèves utiliseront les blocs [Spin for] dans VEXcode GO, comme indiqué ici, pour faire tourner les moteurs connectés aux roues et faire avancer le robot. Les blocs [Spin for] acceptent les « tours » ou les « degrés » comme paramètres. Dans le laboratoire 4, les élèves calculeront le nombre de tours à effectuer dans ce projet pour conduire leur robot sur la distance du parcours du défilé.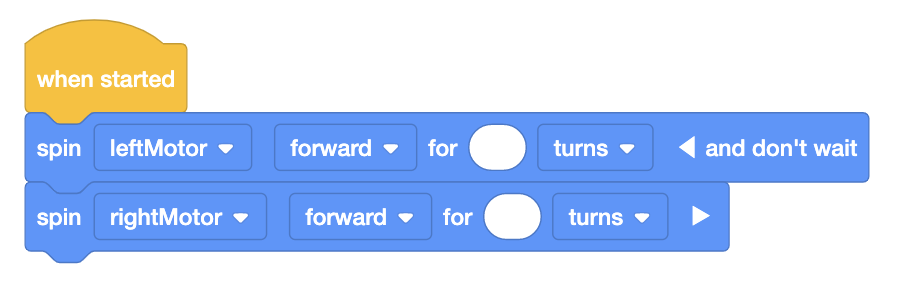 Un projet VEXcode GO commence par un bloc When started et comporte deux blocs Spin for attachés avec le paramètre de distance vide. Les blocs indiquent : Au démarrage, faites tourner le moteur gauche vers l'avant pour des virages à blanc et n'attendez pas ; puis faites tourner le moteur droit vers l'avant pour des virages à blanc.

Regardez la vidéo ci-dessous pour savoir comment calculer le nombre de tours de roue nécessaires pour conduire votre robot en ligne droite sur une distance définie.

Références utiles :

Terminologie et valeurs des roues grises :

Terme	Définition	Visuel	Formule	Valeur
Diamètre	Mesure d'une ligne droite passant par le centre d'un cercle		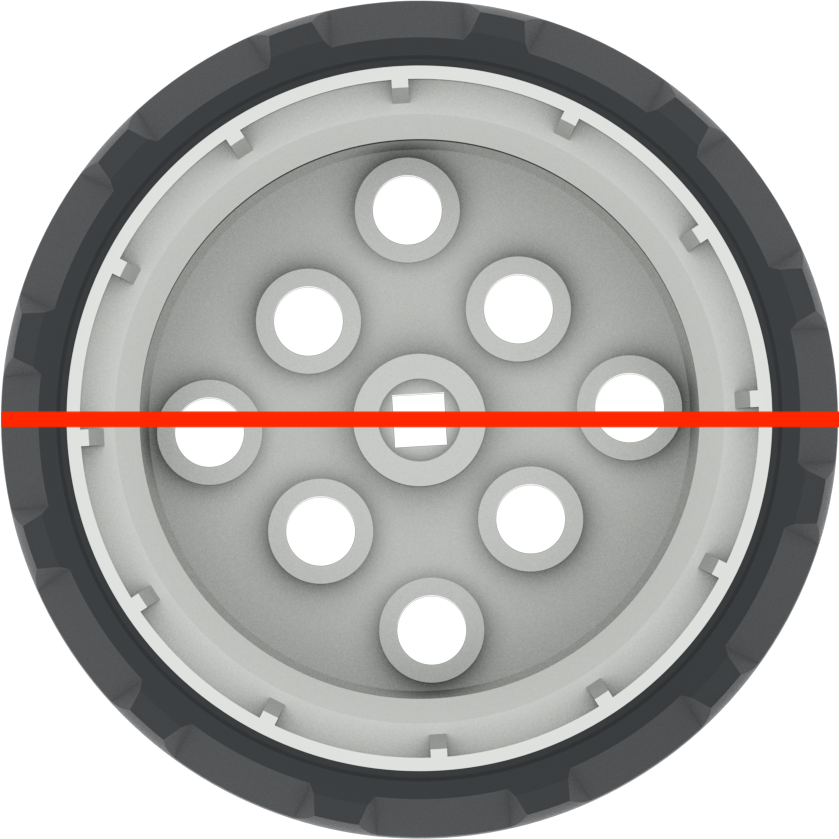d = 2 r	~ 50,93 mm ou 2 pouces
Circonférence	La distance totale autour de l'extérieur d'un cercle		C = πd	~ 160 mm ou 6,25 pouces

Mesurer avec précision

Lorsque les élèves mesurent, assurez-vous de les guider pour qu’ils mesurent avec soin et précision. Vous pouvez utiliserla règle imprimable VEX GOpour que les élèves puissent mesurer, ou des règles de classe.

Rappelez aux élèves de commencer à mesurer à partir du point zéro sur la règle, et de porter une attention particulière au point final de l’objet qu’ils mesurent. Commencer ou terminer leurs mesures de manière inexacte affectera leurs calculs et le mouvement éventuel de leur robot.

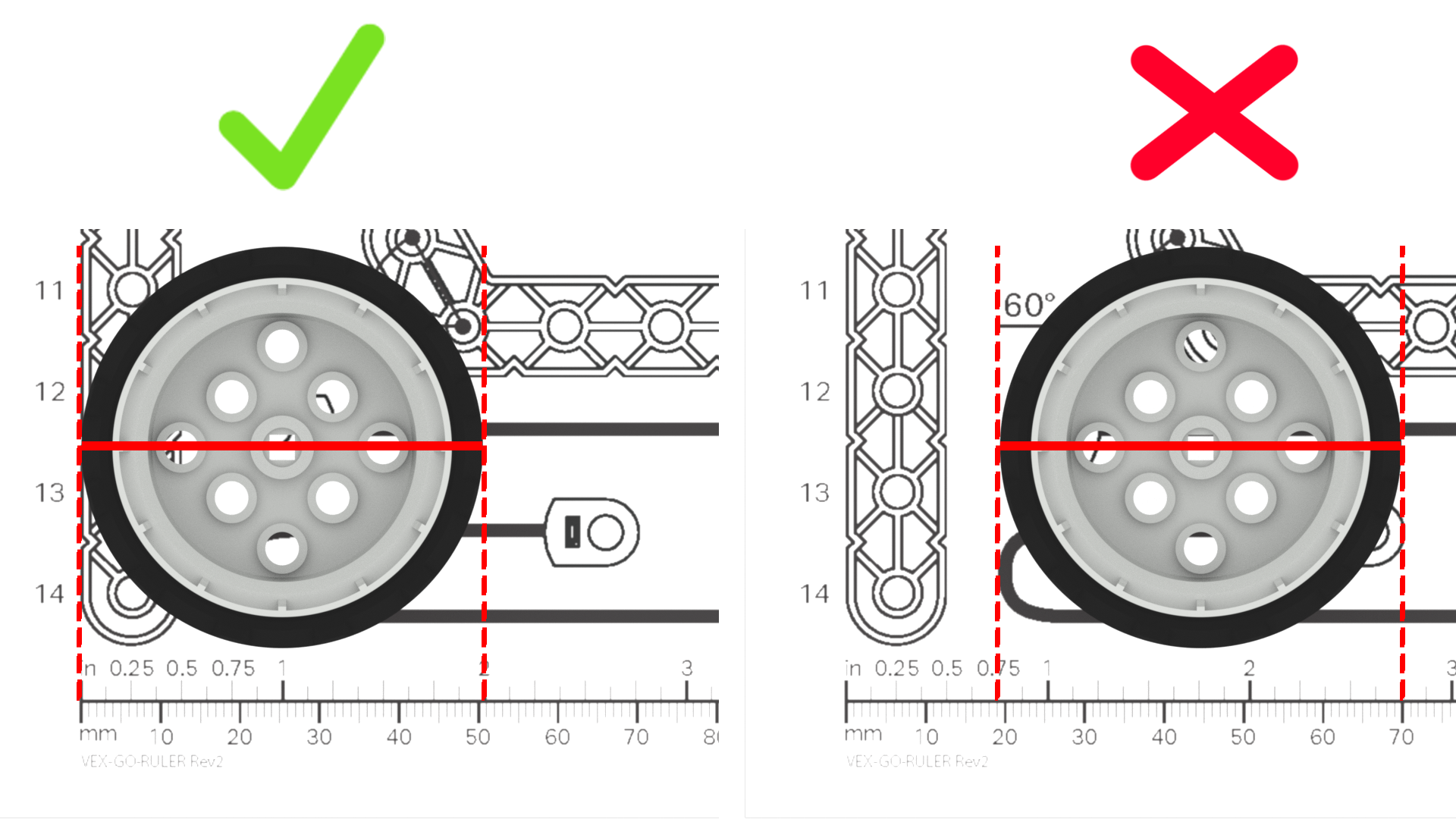
Un schéma indique comment aligner avec précision une roue VEX GO sur la règle imprimable. Sur le côté gauche, une coche verte indique le bon alignement - la roue est posée sur la règle, avec une ligne rouge indiquant le diamètre et des lignes pointillées indiquant l'alignement du bord gauche et droit de la roue avec la marque 0 de la règle et environ 50 mm. À droite, un x rouge indique un alignement incorrect, avec la même roue et les mêmes lignes affichées mais la règle est marquée à environ 19 et 70 mm. — Une roue GO affichée correctement et incorrectement alignée sur la règle VEX GO

Assurez-vous que les élèves savent lire les marques sur la règle qu’ils utilisent, afin de mesurer avec précision. Si les règles que vous utilisez ont à la fois des unités impériales et métriques (comme la règle imprimable VEX GO) être sûr que les élèves utilisent systématiquement les mêmes unités de mesure.

Règle imprimable VEX GO avec unités impériales surlignées en bleu et unités métriques surlignées en vert — Règle imprimable VEX GO avec les unités impériales surlignées en bleu et les unités métriques surlignées en vert

Les élèves peuvent arrondir leurs mesures à l’unité la plus proche, ou à une fraction d’unité. L'arrondi peut simplifier les calculs, si nécessaire, mais peut également rendre les mesures moins précises. Par exemple, vous pouvez demander aux élèves d’arrondir au demi-pouce ou au centimètre le plus proche, mais leur robot se déplace légèrement plus loin que prévu initialement. Alternativement, vous pouvez demander aux élèves de mesurer au ⅛ de pouce ou au millimètre le plus proche et de constater que leurs robots se déplacent plus près de la distance prévue.
If students need extra practice with measuring, vous pouvez utiliser le Pratique Mesure de l'activité VEX GO avec des étudiants individuels ou des groupes, ou dans le cadre d’une activité en classe entière.

Mathématiques de la rotation à 360°

Pour compléter le défilé du laboratoire 5, les élèves conduiront leur char Code Base le long d'un itinéraire de défilé avec un virage.

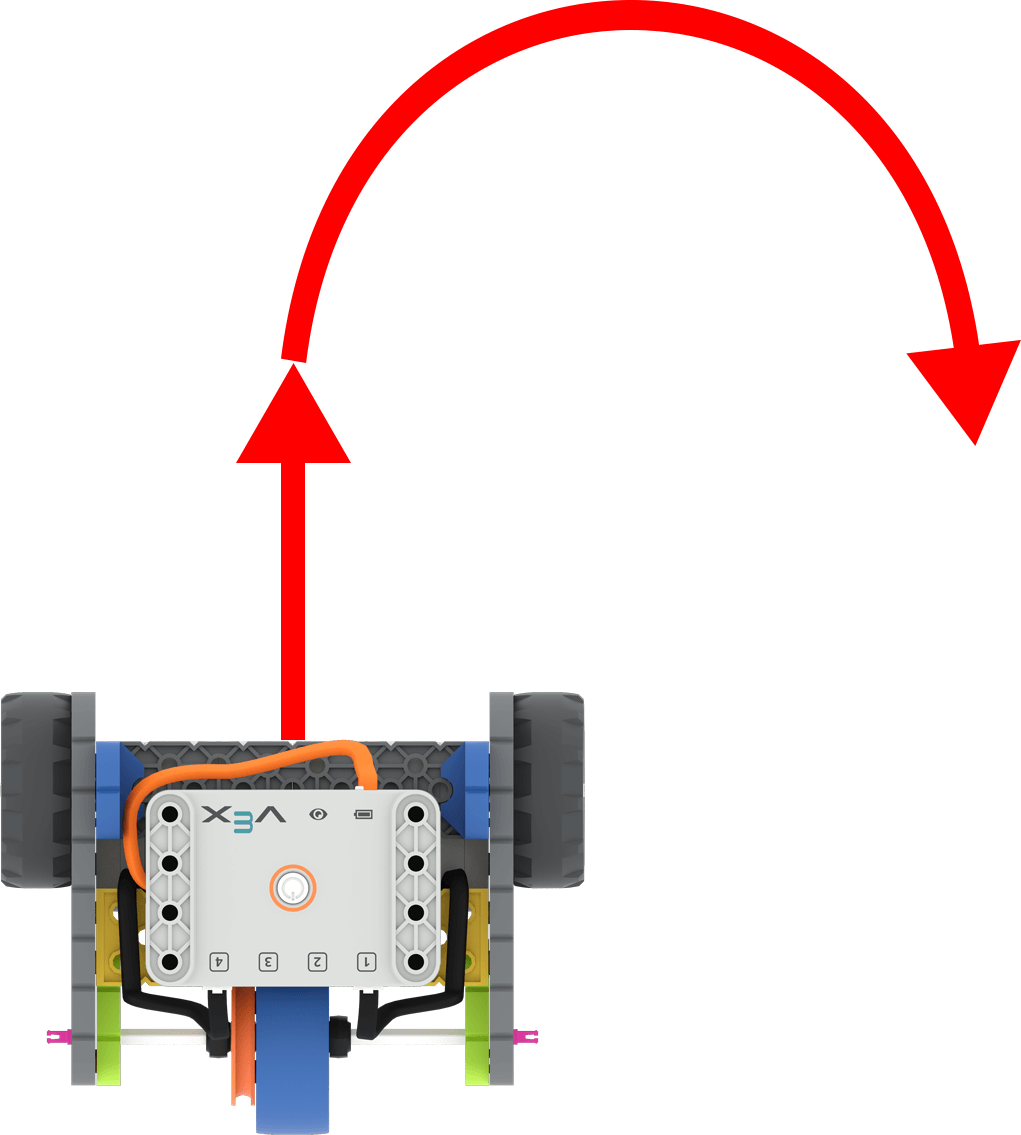
Code de base avec une flèche s'étendant de l'avant du robot, pour indiquer les mouvements de marche avant puis de virage à droite.

Code de base avec des flèches pour montrer la conduite en marche avant puis le virage à droite

Les élèves s'appuieront sur ce qu'ils ont appris sur le codage du robot pour parcourir une distance en ligne droite, pour coder le robot pour parcourir une distance non linéaire ou pour effectuer un virage. Les élèves calculent toujours le nombre de tours nécessaires pour parcourir une distance donnée, ils utiliseront donc la même formule que dans le laboratoire précédent.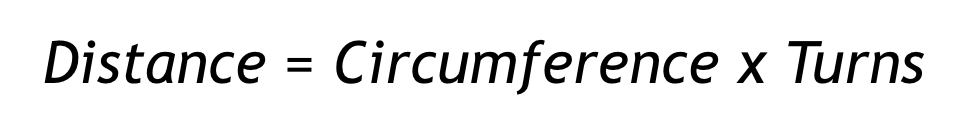 Une formule dit : « la distance est égale à la circonférence multipliée par les tours ».

Regardez la vidéo ci-dessous pour apprendre à calculer le nombre de tours de roue nécessaires pour effectuer un tour de 360° du robot avec vos élèves.

Références utiles :

Lorsque la base de code tourne, les roues motrices se déplacent dans des directions opposées pour faire tourner le robot. Par exemple, pour faire tourner le robot vers la droite, la roue gauche avancera, tandis que la roue droite avancera en marche arrière.

Terminologie et valeurs pour la base de code :

Terme	Définition	Visuel	Formule	Valeur
Diamètre	Mesure d'une ligne droite à partir du centre de chaque roue (également appelé empattement)		d = 2 r	~ 135 mm ou 5,3 pouces
Circonférence	La distance totale parcourue par les roues pour effectuer un 360°		C = πd	~ 424 mm ou 16,7 pouces

Mathématiques pour réussir n'importe quel diplôme

Regardez cette vidéo pour en savoir plus sur le calcul du nombre de tours de roue nécessaires au robot pour tourner d'un degré.

Conversion en degrés
Le bloc [Spin for] acceptera les tours ou les degrés comme paramètres. Pour utiliser les degrés, multipliez simplement le nombre de tours par 360. Cet exemple montre le nombre de degrés que les moteurs devront tourner pour faire tourner le robot à°. Notez que dans ce projet, les moteurs tournent dans des directions opposées et que le « et n'attendez pas » est ajouté au premier bloc, de sorte que les moteurs tournent simultanément. Cela fera tourner le robot vers la droite pour obtenir les 360° souhaités. 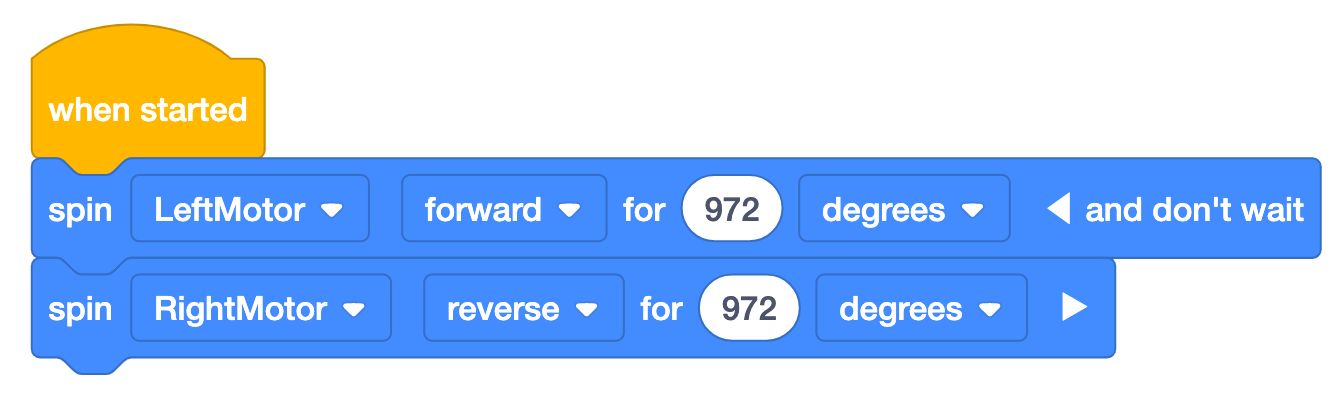Le projet VEXcode GO commence par un bloc When started avec deux blocs Spin for attachés. Les blocs indiquent : Au démarrage, faites tourner le moteur gauche vers l'avant sur 972 degrés et n'attendez pas ; puis faites tourner le moteur droit vers l'arrière sur 972 degrés.

Idées fausses courantes

Les étudiants peuvent avoir plusieurs idées fausses sur la mesure et les mathématiques de la conduite et des virages. Voici quelques-uns des problèmes les plus courants, avec des sur la manière de les aborder avec vos élèves.

Situation	Idée fausse	Correction suggérée
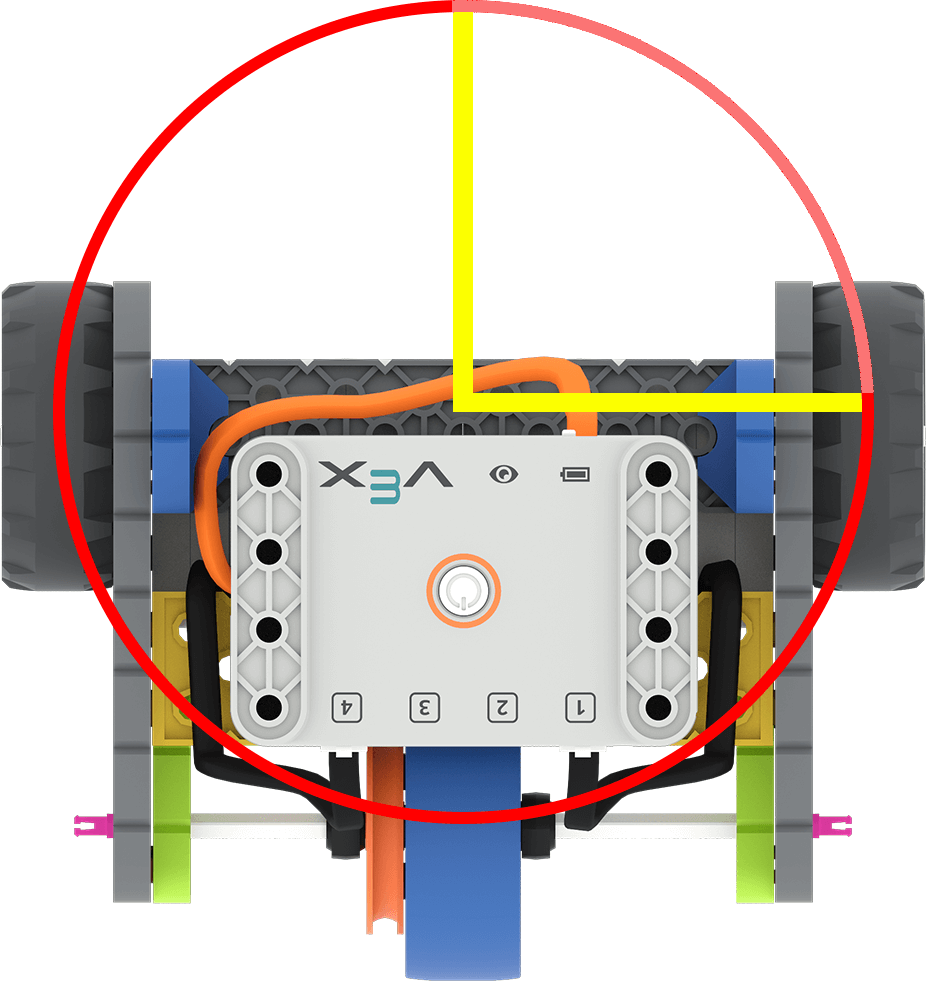
L'enseignant demande à la classe, que devons-nous saisir dans le bloc [Tourner pour] pour faire tourner le robot de 90° ? L’élève répond « 90 ».	La distance en degrés parcourue par la roue pour effectuer un virage est égale à l'angle de virage. Les élèves n’utilisent pas la circonférence de braquage du robot pour calculer la distance en degrés que la roue doit parcourir.	Rappelez aux élèves que les roues doivent tourner le long de la circonférence de braquage pour que le robot puisse tourner. (Dans cette image, c'est le long du cercle rouge d'une ligne jaune à l'autre.) Tournez la roue elle-même de 90° seulement pour aider les élèves à visualiser jusqu'où la roue tourne pour parcourir une distance donnée.
L'enseignant demande à la classe, que devons-nous saisir dans le bloc [Tourner pour] pour faire avancer le robot de 12 pouces ? L’élève répond « 12 ».	Le nombre de tours de roue est égal à la distance de conduite souhaitée. L'élève n'utilise pas la circonférence de la roue pour calculer le nombre de tours de roue nécessaires pour parcourir la distance souhaitée.	Rappelez aux élèves la distance parcourue par le robot avec un tour de roue et demandez-leur si 12 tours complets semblent trop ou trop peu pour parcourir 12 pouces. Pour aider les élèves à mieux visualiser cela, faites rouler une roue le long d’une règle pendant 12 tours de roue, pour montrer aux élèves à quelle distance se trouve cette distance. Rappelez aux élèves qu’un tour de roue correspond à la circonférence de la roue et que 12 pouces doivent être divisés par cette circonférence.
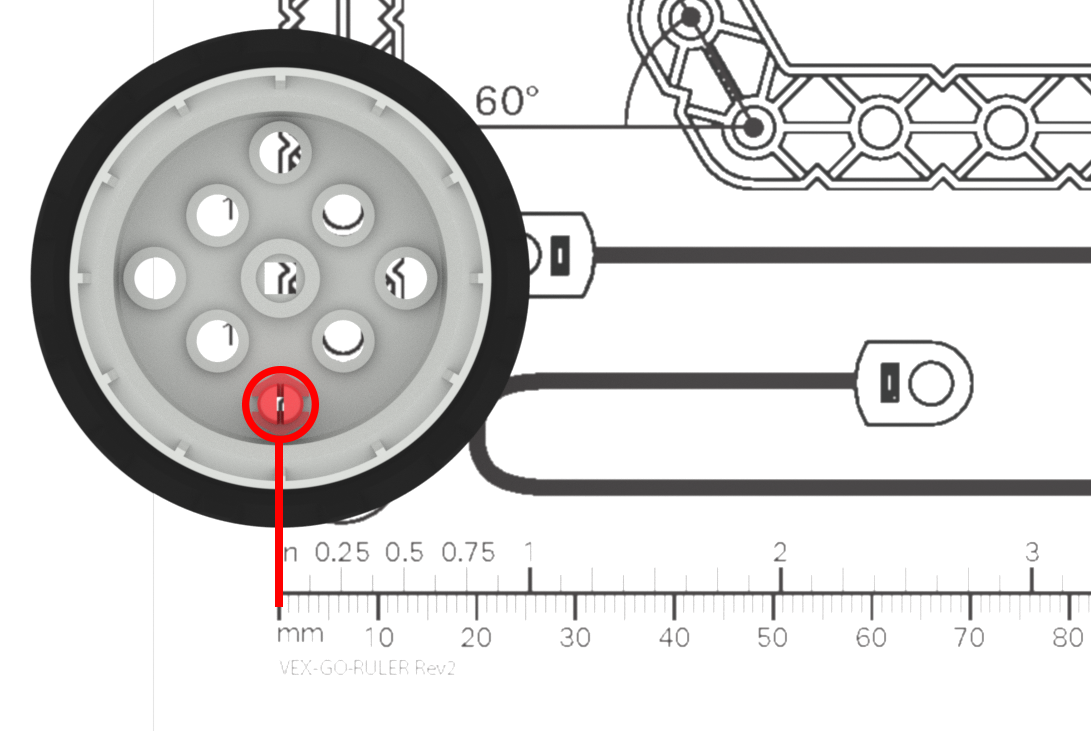
L'élève mesure la roue, mais des bords de lane se trouve sur la marque zéro de la règle.	La règle commence à 1 et non à zéro. L'élève n'utilise pas correctement la règle afin d'obtenir une mesure précise.	Rappelez aux élèves que la règle commence à la marque « 0 » et que s’ils ne mesurent pas à partir de ce point, leurs mesures seront incorrectes. Vous pouvez marquer le début de la règle avec du ruban adhésif ou un marqueur de couleur, comme aide visuelle supplémentaire pour les élèves pendant qu'ils travaillent. (Pour une pratique supplémentaire avec mesurer, les élèves peuvent compléter le Pratique Activité de mesure.)
Un étudiant dit que son projet ne fonctionne pas. L'enseignant remarque que le nombre correct de tours de roue se trouve dans le bloc [Tourner pour], mais le paramètre est défini sur « degrés ».	Les unités ou les paramètres sont interchangeables. Les étudiants ne prêtent pas attention aux paramètres/unités de mesure dans leur projet.	Demandez aux élèves quelle unité de mesure ils utilisent et si cela correspond au paramètre du bloc. Rappelez aux élèves que leurs calculs ne fonctionneront comme prévu que si le paramètre est défini sur l’unité correcte. Les tours et les degrés n'ont pas la même valeur.
Un élève essaie d'entrer « 21/4 » dans le paramètre du bloc [Spin for], pour entrer « 2 ¼ tours ».	Les fractions et les décimales s'écrivent de la même manière. L’élève ne convertit pas la fraction en décimal.	Rappelez aux élèves qu’ils doivent convertir les fractions en décimales pour qu’elles soient des paramètres reconnaissables. Pour ce faire, divisez le numérateur par le dénominateur. 2 ¼=94 =2,25 Vous pouvez demander aux élèves de dresser un tableau des valeurs fractionnaires fréquemment utilisées et de leurs équivalents décimaux pour créer leur propre ressource.
L’enseignant demande aux élèves de partager leur calcul de circonférence de roue. Réponses des étudiants ~ 83,2 mm.	La circonférence est calculée en utilisant le rayon -πxrayon. L'élève utilise la mauvaise mesure dans le calcul.	Rappelez aux élèves que la circonférence est π x diamètre; et le diamètre est une ligne droite passant par le centre de la roue (ou deux fois le rayon).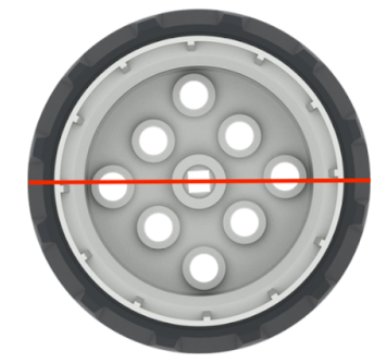 Vous souhaiterez peut-être mesurer et calculer la valeur dans le cadre d’une activité en classe entière. si de nombreux élèves ont des difficultés à utiliser les formules.

Situation

Idée fausse

Correction suggérée

L'enseignant demande à la classe, que devons-nous saisir dans le bloc [Tourner pour] pour faire tourner le robot de 90° ?

L’élève répond « 90 ».

La distance en degrés parcourue par la roue pour effectuer un virage est égale à l'angle de virage.

Les élèves n’utilisent pas la circonférence de braquage du robot pour calculer la distance en degrés que la roue doit parcourir.

Rappelez aux élèves que les roues doivent tourner le long de la circonférence de braquage pour que le robot puisse tourner. (Dans cette image, c'est le long du cercle rouge d'une ligne jaune à l'autre.)

L'image de haut en bas de la base de code avec le cercle en haut indiquant la circonférence. Les lignes jaunes à 12 heures et à 3 heures délimitent 90 degrés du cercle entier.

Tournez la roue elle-même de 90° seulement pour aider les élèves à visualiser jusqu'où la roue tourne pour parcourir une distance donnée.

L'enseignant demande à la classe, que devons-nous saisir dans le bloc [Tourner pour] pour faire avancer le robot de 12 pouces ?

L’élève répond « 12 ».

Le nombre de tours de roue est égal à la distance de conduite souhaitée.

L'élève n'utilise pas la circonférence de la roue pour calculer le nombre de tours de roue nécessaires pour parcourir la distance souhaitée.

Rappelez aux élèves la distance parcourue par le robot avec un tour de roue et demandez-leur si 12 tours complets semblent trop ou trop peu pour parcourir 12 pouces.

Pour aider les élèves à mieux visualiser cela, faites rouler une roue le long d’une règle pendant 12 tours de roue, pour montrer aux élèves à quelle distance se trouve cette distance.

Un schéma montre une roue VEX GO avec une broche rouge dans le moyeu au-dessus de la règle imprimable. La broche est alignée avec la marque 0 mm de la règle VEX GO, montrant comment marquer avec précision un tour de roue.

Rappelez aux élèves qu’un tour de roue correspond à la circonférence de la roue et que 12 pouces doivent être divisés par cette circonférence.

L'élève mesure la roue, mais des bords de lane se trouve sur la marque zéro de la règle.

La règle commence à 1 et non à zéro.

L'élève n'utilise pas correctement la règle afin d'obtenir une mesure précise.

Rappelez aux élèves que la règle commence à la marque « 0 » et que s’ils ne mesurent pas à partir de ce point, leurs mesures seront incorrectes.

Vous pouvez marquer le début de la règle avec du ruban adhésif ou un marqueur de couleur, comme aide visuelle supplémentaire pour les élèves pendant qu'ils travaillent. (Pour une pratique supplémentaire avec mesurer, les élèves peuvent compléter le Pratique Activité de mesure.)

Un étudiant dit que son projet ne fonctionne pas.

L'enseignant remarque que le nombre correct de tours de roue se trouve dans le bloc [Tourner pour], mais le paramètre est défini sur « degrés ».

Les unités ou les paramètres sont interchangeables.

Les étudiants ne prêtent pas attention aux paramètres/unités de mesure dans leur projet.

Demandez aux élèves quelle unité de mesure ils utilisent et si cela correspond au paramètre du bloc.

Un VEXcode GO Spin pour bloc avec la liste déroulante des paramètres d'unité ouverte et les degrés sélectionnés. Le bloc lit Spin Motor1 vers l'avant sur 90 degrés. Rappelez aux élèves que leurs calculs ne fonctionneront comme prévu que si le paramètre est défini sur l’unité correcte. Les tours et les degrés n'ont pas la même valeur.

Un élève essaie d'entrer « 21/4 » dans le paramètre du bloc [Spin for], pour entrer « 2 ¼ tours ».

Les fractions et les décimales s'écrivent de la même manière.

L’élève ne convertit pas la fraction en décimal.

Rappelez aux élèves qu’ils doivent convertir les fractions en décimales pour qu’elles soient des paramètres reconnaissables. Pour ce faire, divisez le numérateur par le dénominateur.
2 ¼=94 =2,25
Vous pouvez demander aux élèves de dresser un tableau des valeurs fractionnaires fréquemment utilisées et de leurs équivalents décimaux pour créer leur propre ressource.

L’enseignant demande aux élèves de partager leur calcul de circonférence de roue.

Réponses des étudiants
~ 83,2 mm.

La circonférence est calculée en utilisant le rayon -πxrayon.

L'élève utilise la mauvaise mesure dans le calcul.

Rappelez aux élèves que la circonférence est π x diamètre; et le diamètre est une ligne droite passant par le centre de la roue (ou deux fois le rayon).
A top down diagram of the VEX GO Wheel with a red line across the center indicating the diameter of the wheel.

A top down diagram of the VEX GO Wheel with a red line across the center indicating the diameter of the wheel.

Vous souhaiterez peut-être mesurer et calculer la valeur dans le cadre d’une activité en classe entière. si de nombreux élèves ont des difficultés à utiliser les formules.

Exemples de solutions

Exemple de solution du laboratoire 4

*Remarque : L'expression « et n'attendez pas » est utilisée avec le premier bloc de l'exemple de projet afin que les deux blocs s'exécutent simultanément. Sans « et n'attendez pas », le premier moteur tournerait, puis le deuxième, et la base de code ne fonctionnerait pas comme prévu. Assurez-vous que les étudiants ne réduisent PAS le « et n'attendez pas » sinon leur projet ne se déroulera pas comme prévu.

Parcours du défilé constitué de 5 tuiles VEX GO connectées sur une ligne horizontale. Il y a des lignes rouges sur les première et dernière lignes noires verticales sur les tuiles, indiquant le début et la fin à 48 pouces d'intervalle. La base de code est affichée dans la position de départ avec les roues alignées sur la ligne rouge à l'extrême droite.

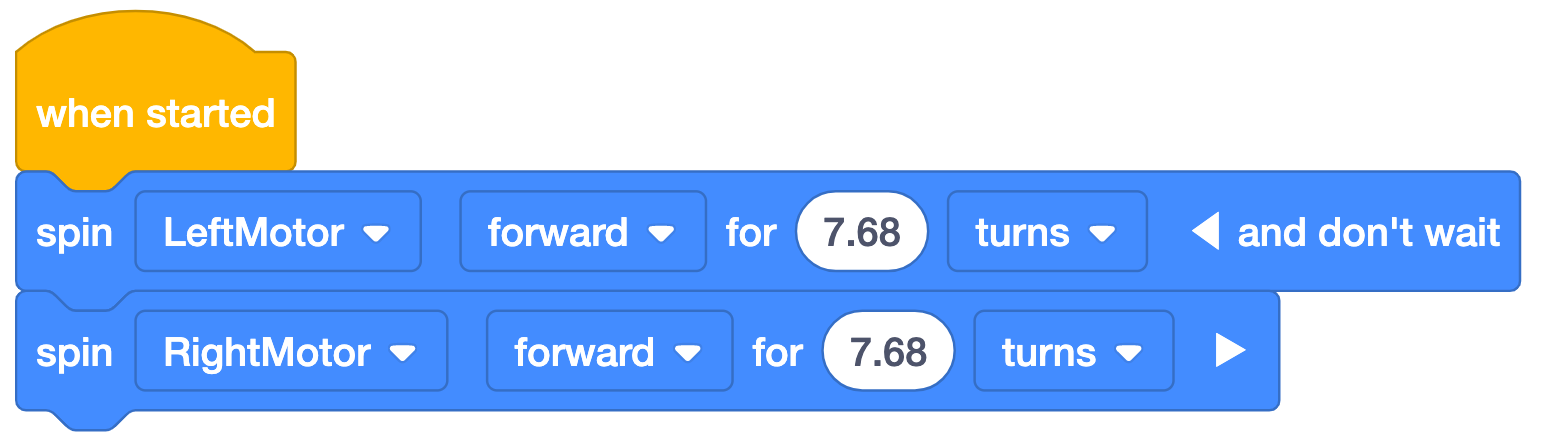
Pour parcourir la longueur de 48 pouces (~122 cm) du parcours du défilé, la Code Base devra parcourir ~7,68 tours. Le calcul est affiché à gauche et l'exemple de solution VEXcode GO à droite.
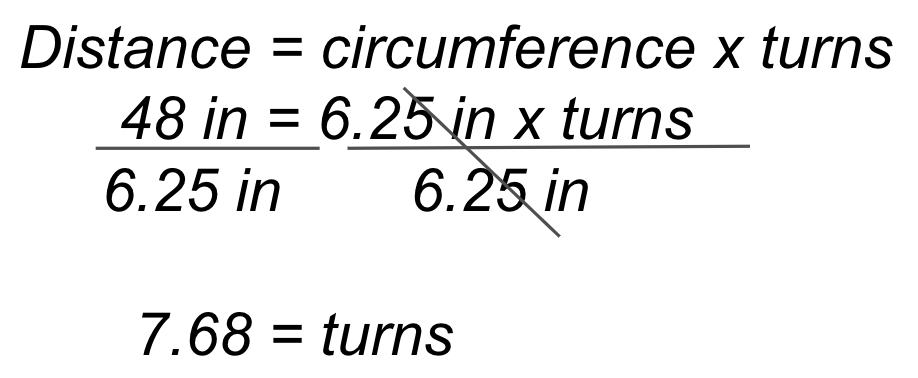
Un exemple de solution indique que la distance est égale à la circonférence multipliée par les tours de roue, avec les valeurs ci-dessous indiquant 48 pouces = 6,25 pouces multiplié par les tours. Les deux côtés de l'équation sont divisés par 6,25 pouces, ce qui donne 7,68 tours égaux. Un projet VEXcode GO commence par un bloc When started et possède deux blocs Spin for attachés. Les blocs indiquent : Au démarrage, faites tourner le moteur gauche vers l'avant pendant 7,68 tours et n'attendez pas ; puis faites tourner le moteur droit vers l'avant pendant 7,68 tours.

Exemple de solution du laboratoire 5

Pour parcourir la longueur de 48 pouces (~ 122 cm) du parcours du défilé et tourner à 180 degrés, la base de code devra avancer pendant ~ 7,68 tours, puis tourner un moteur vers l'avant et l'autre vers l'arrière pendant ~ 1,47 tours. Le calcul est présenté à côté de l'exemple de solution VEXcode GO sur la droite.

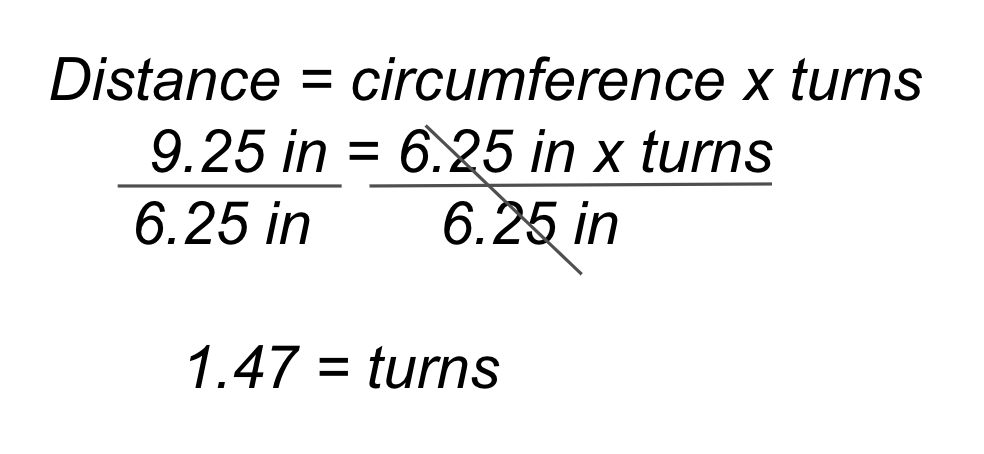
Un exemple de solution indique que la distance est égale à la circonférence multipliée par les tours de roue, avec les valeurs ci-dessous indiquant 9,25 pouces = 6,25 pouces multiplié par les tours. Les deux côtés de l'équation sont divisés par 6,25 pouces, ce qui donne 1,47 tours.

Remarque : pour utiliser des degrés au lieu de tours, les calculs de tours par 360.

Prolongation du parcours du défilé

Si les élèves ont besoin d’un défi supplémentaire, vous pouvez prolonger le parcours du défilé de différentes manières. Voici un exemple, avec une solution possible.

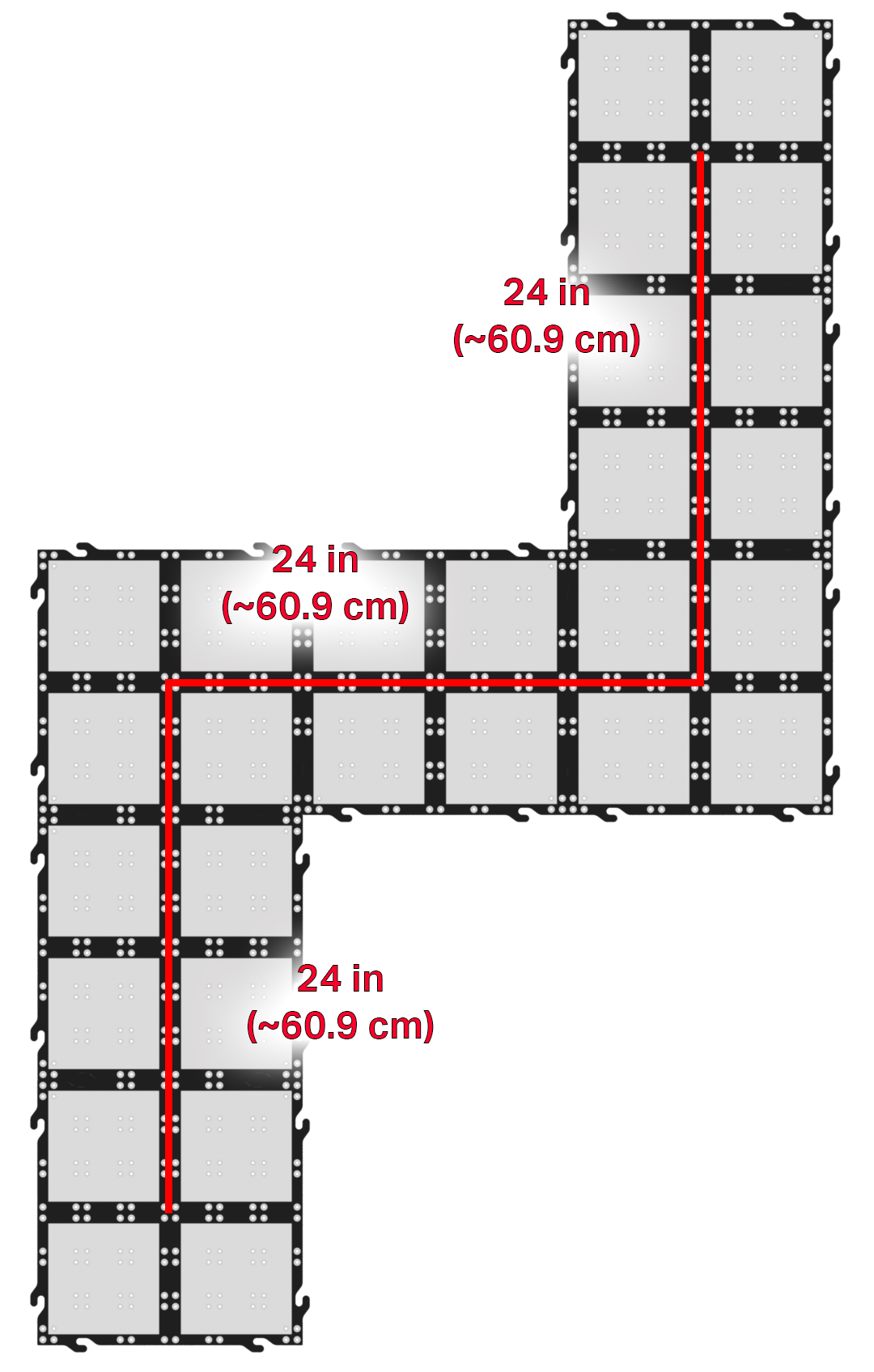
Un schéma de l'extension du parcours du défilé montrant les 7 tuiles VEX GO connectées pour former un itinéraire qui s'étend verticalement sur 24 pouces, tourne vers la droite et s'étend horizontalement sur 24 pouces, puis tourne vers la gauche et s'étend verticalement sur 24 pouces. — Exemple d'une extension possible du parcours du défilé

Dans cet exemple d'itinéraire, les distances de conduite et les virages sont réduits de moitié par rapport aux laboratoires. Sur cet itinéraire, cependant, le sens des virages est important. En plus de recalculer, les élèves devront déterminer les directions pour faire tourner les roues dans la direction souhaitée.
Les calculs divisés par deux des laboratoires précédents sont les suivants :

Distance de conduite = ~ 3,84 tours
Distance de virage = ~ 0,73 tours

Ces valeurs sont utilisées dans l'exemple de solution VEXcode GO suivant :

< Arrière Retour aux laboratoires Suivant >