M.A.D. เฟืองของกล่อง
ขั้นตอนที่ 1: M.A.D. ขั้นตอนที่ 2 ของกล่อง: เฟืองฟันน้ำนม 12 และ 36
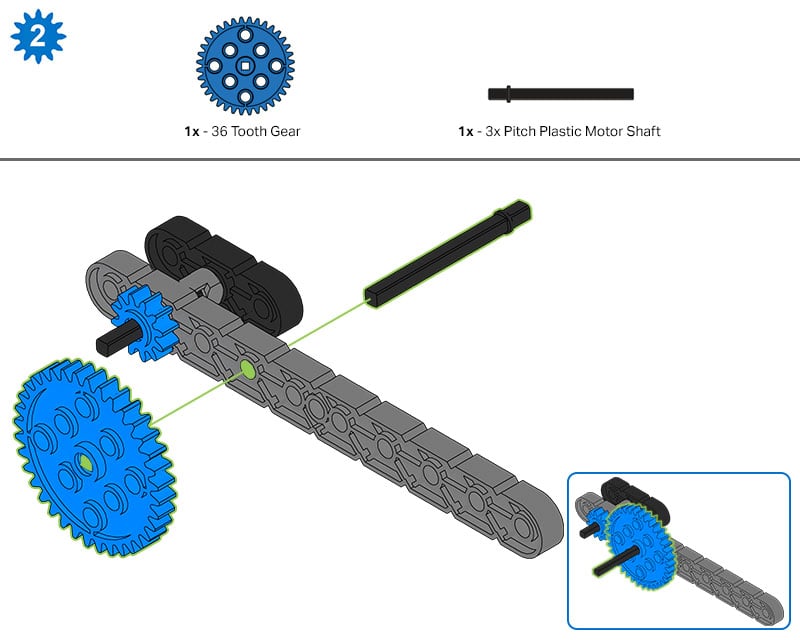
ในขั้นตอนที่ 2 ของคำแนะนำในการสร้างฟันเฟือง 12 ซี่อยู่บนเพลาที่เชื่อมต่อ M.A.D. แล้ว ที่จับของบ็อกซ์ที่ด้านนั้นของบิลด์
- สร้าง Expert หาด้านนั้นของ M.A.D. กล่องและแสดงให้เพื่อนร่วมทีมของคุณเห็น จากนั้นแสดงให้เห็นว่าเมื่อหมุนด้ามจับนั้นเพลาจะหมุนเฟือง 12 ซี่ (เฟืองขับ - อินพุต) ซึ่งจะหมุนเฟือง 36 ซี่ (เฟืองขับ - เอาต์พุต) ที่กำลังถูกเพิ่มในขั้นตอนนี้ของการสร้าง
- อัตราทดเกียร์ของเกียร์สองตัวนี้เป็นเท่าไหร่?
- เครื่องคิดเลขหาสมการด้านล่างและให้ผู้บันทึกตรวจสอบ
![]() กล่องเครื่องมือครู
- การ
แก้ปัญหา
กล่องเครื่องมือครู
- การ
แก้ปัญหา
เครื่องคิดเลขและเครื่องบันทึกในกลุ่มควรตระหนักว่าการคำนวณควรเสร็จสมบูรณ์ดังนี้:
-
เศษส่วนแรกควรเป็น 36/12
-
เศษส่วนที่สองควรเป็น 3/1
อีกครั้งตรวจสอบให้แน่ใจว่านักเรียนเข้าใจวิธีการลดเศษส่วนโดยการดำน้ำทั้งตัวเศษและตัวส่วนด้วยจำนวนเดียวกัน
อัตราส่วน 3: 1 บอกเราว่าเฟืองฟันน้ำนม 12 ตัวต้องหมุนสามครั้งเพื่อหมุนเฟืองฟันน้ำนม 36 ตัวหนึ่งครั้ง
ซึ่งนำไปสู่ข้อได้เปรียบเชิงกลของ แรงบิด แรงบิดคืออะไร?
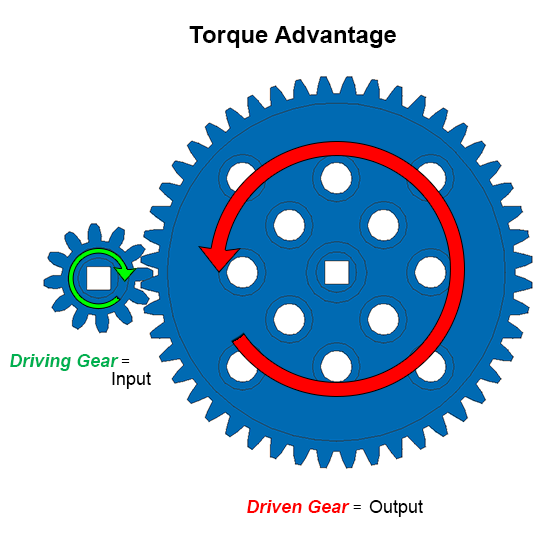
แรงบิดเป็นข้อได้เปรียบทางกลที่ทำให้เอาต์พุตของเกียร์หรือเครื่องจักรที่ขับเคลื่อนมีประสิทธิภาพมากขึ้น ในกรณีนี้พม. Box มีอินพุตมากกว่าเอาต์พุตถึงสามเท่าซึ่งทำให้มีประสิทธิภาพมากขึ้น
- ผู้บันทึกอย่าลืมเพิ่มบันทึกลงในสมุดบันทึกวิศวกรรมเกี่ยวกับข้อได้เปรียบทางกลของแรงบิดภายใน M.A.D. กล่อง
ขั้นตอนที่ 2: M.A.D. ขั้นตอนของกล่อง 10: เฟืองฟันน้ำนม 36 และ 12
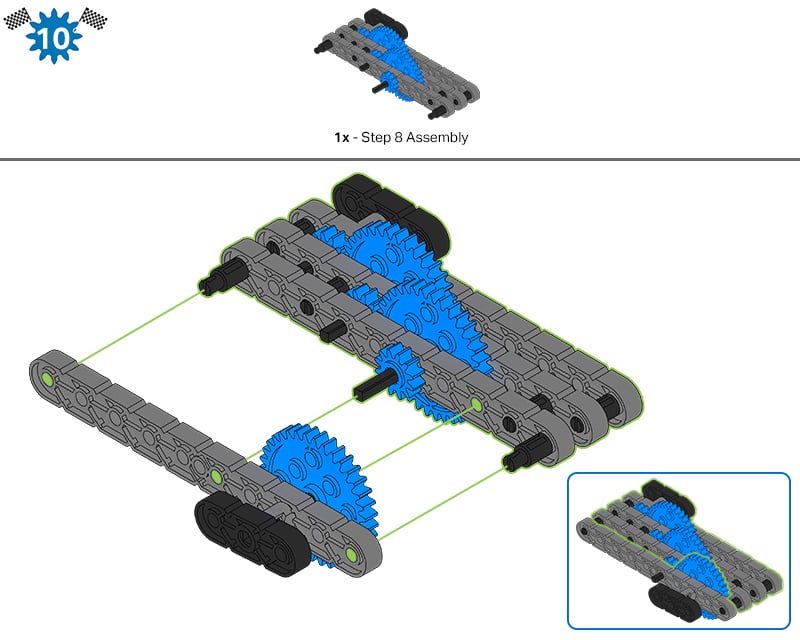
ในขั้นตอนที่ 10 ของคำแนะนำในการสร้างอีกด้านหนึ่งของ M.A.D. เชื่อมต่อกล่องแล้ว มันมีเฟือง 36 ฟันบนเพลาพร้อมด้ามจับ
- สร้าง Expert หาด้านนั้นของ M.A.D. กล่องและแสดงให้กลุ่มดู จากนั้นแสดงให้เห็นว่าเมื่อหมุนด้ามจับนั้นเพลาจะหมุนเฟือง 36 ซี่ (เฟืองขับ - อินพุต) ซึ่งจะหมุนเฟือง 12 ซี่ (เฟืองขับ - เอาต์พุต)
- อัตราทดเกียร์ของเกียร์สองตัวนี้เป็นเท่าไหร่?
- เครื่องคิดเลขหาสมการด้านล่างแล้วให้ผู้บันทึกตรวจสอบ
![]() กล่องเครื่องมือครู
- การ
แก้ปัญหา
กล่องเครื่องมือครู
- การ
แก้ปัญหา
เครื่องคิดเลขและเครื่องบันทึกในกลุ่มควรตระหนักว่าการคำนวณควรเสร็จสมบูรณ์ดังนี้:
-
เศษส่วนแรกควรเป็น 12/36
-
เศษส่วนที่สองควรเป็น 1/3
อีกครั้งตรวจสอบให้แน่ใจว่านักเรียนเข้าใจวิธีลดเศษส่วนโดยการดำน้ำทั้งตัวเศษและตัวส่วนด้วยจำนวนเดียวกัน
อัตราส่วน 1: 3 บอกเราว่าการขับ 36 ฟันเฟืองต้องหมุนเพียงครั้งเดียวเพื่อหมุน 12 ฟันเฟืองสามครั้ง
ซึ่งนำไปสู่ข้อได้เปรียบทางกลของ ความเร็ว
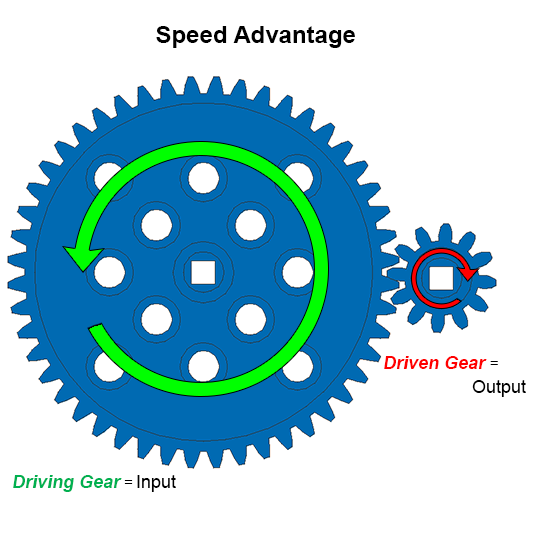
ความเร็วเป็นข้อได้เปรียบทางกลที่ทำให้เอาต์พุตของเกียร์หรือเครื่องจักรที่ขับเคลื่อนเร็วขึ้น ในกรณีนี้พม. Box มีเอาต์พุตมากกว่าการหมุนอินพุตถึงสามเท่าซึ่งทำให้ทำงานได้เร็วขึ้น
- ผู้บันทึกให้แน่ใจว่าได้เพิ่มบันทึกลงในสมุดบันทึกวิศวกรรมเกี่ยวกับข้อได้เปรียบทางกลของความเร็วภายใน M.A.D. กล่อง
ขั้นตอนที่ 3: M.A.D. อัตราส่วนเกียร์แบบผสมของกล่อง
- สร้างผู้เชี่ยวชาญหมุนด้ามจับที่เชื่อมต่อกับเฟือง 36 ซี่อย่างช้าๆและให้กลุ่มดูว่าด้ามจับอื่นหมุนเร็วแค่ไหน
- เครื่องบันทึก, หลังจากอ่านคำอธิบายด้านล่าง, อธิบายว่าอัตราส่วนเฟืองของสารประกอบคืออะไรในสมุดบันทึกทางวิศวกรรม
อัตราทดเกียร์สำหรับเฟือง 36 ซี่ที่หมุนเฟือง 12 ซี่คือ 1: 3 ด้วยข้อได้เปรียบทางกลของความเร็ว แต่เมื่อคุณหมุนด้ามจับที่เชื่อมต่อกับเฟือง 36 ซี่หนึ่งครั้งด้ามจับอีกอันจะหมุนมากกว่าสามครั้ง
นั่นเป็นเพราะพม. กล่องใช้อัตราส่วนเกียร์ของ สารประกอบ M.A.D. อัตราส่วนเฟืองผสมของกล่องถูกสร้างขึ้นโดยมี 36 ฟันเฟืองและ 12 ฟันเฟืองใช้เพลาเดียวกันอัตราส่วน
เกียร์ของสารประกอบคูณความได้เปรียบเชิงกลของความเร็วหรือแรงบิดภายในกลไก
![]() เคล็ดลับสำหรับครู
เคล็ดลับสำหรับครู
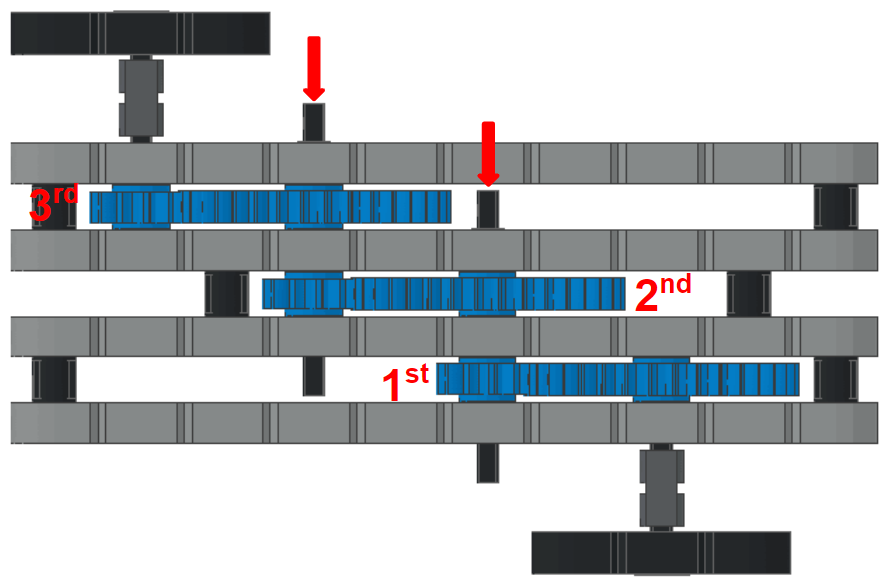
ฉลากลำดับที่ 1, 2 และ 3 สำหรับอัตราทดเกียร์ในภาพ M.A.D. กล่องด้านบนขึ้นอยู่กับการหมุนด้ามจับที่เชื่อมต่อกับเฟืองฟัน 36 ซี่ นั่นคือด้ามจับที่ด้านล่างของภาพนะคะ
ลูกศรสีแดงในภาพด้านบนแสดงเพลาที่มีทั้ง 36 ฟันและ 12 ฟันเฟือง เพลาเหล่านั้นเชื่อมต่ออัตราส่วนเกียร์หนึ่ง, สองและสามเข้าด้วยกัน เมื่อเพลาหมุนทั้งเฟือง 12 ฟันและ 36 ฟันบนเพลาหมุน
สิ่งนี้จะทวีคูณความได้เปรียบทางกลที่สร้างขึ้นโดยอัตราทดเกียร์แต่ละตัวเนื่องจากเชื่อมต่อเข้ากับอัตราทดเกียร์
แบบผสม M.A.D. BOX มีอัตราส่วนเกียร์ของสารประกอบสองตัวเนื่องจากคุณสามารถให้อินพุตบนด้านใดด้านหนึ่ง - ด้านหนึ่งนำไปสู่ข้อได้เปรียบด้านแรงบิดและอีกด้านหนึ่งนำไปสู่ข้อได้เปรียบด้านความเร็ว
เพื่อคำนวณอัตราส่วนเกียร์ของสารประกอบบนด้านหนึ่งของ M.A.D. กล่องเราต้องหาอัตราส่วนเกียร์สามตัวในบิลด์จากอินพุตนั้นไปยังเอาต์พุตแล้วคูณเข้าด้วยกัน
- สร้างผู้เชี่ยวชาญค้นหาด้านข้างของ M.A.D. กล่องที่ด้ามจับอินพุตหมุนเฟือง 36 ฟันและแสดงให้กลุ่มดู คำแนะนำ: เป็นที่จับที่ด้านล่างของภาพด้านบน ชี้ให้เห็นในบิลด์เพื่อตรวจสอบว่าอัตราส่วนเกียร์ทั้งสามถูกพบที่ไหน
- จำไว้ว่าเฟืองขับทั้งหมดเป็น 36 ฟันเฟืองและเฟืองขับทั้งหมดเป็น 12 ฟันเฟือง
- เครื่องคิดเลขและเครื่องบันทึกให้กรอกและตรวจสอบสมการด้านล่าง:
- ทีมงานทั้งหมดควรพยายามตอบคำถามต่อไปนี้: อัตราส่วนเกียร์ของสารประกอบ 1:27 หมายความว่าอย่างไร? เมื่อด้ามจับที่มีเฟือง 36 ซี่หมุนหนึ่งครั้งควรมีด้ามจับอีกกี่อัน?
- ผู้บันทึกควรจัดระเบียบคำตอบที่ดีที่สุดของทีมและเขียนลงในสมุดบันทึกวิศวกรรม
![]() กล่องเครื่องมือครู
- การ
แก้ปัญหา
กล่องเครื่องมือครู
- การ
แก้ปัญหา
เครื่องคิดเลขและเครื่องบันทึกในกลุ่มควรตระหนักว่าการคำนวณควรเสร็จสมบูรณ์ดังนี้:
-
เศษส่วนที่ขาดหายไปในอัตราส่วนเกียร์หนึ่งคือ 1/3
-
เศษส่วนที่ขาดหายไปในอัตราส่วนเกียร์สองคือ 12/36 และ 1/3
-
เศษส่วนที่ขาดหายไปในอัตราส่วนเกียร์สามคือ 12/36
สมการสำหรับการคำนวณอัตราส่วนเฟืองผสมถูกจัดให้มีไว้เนื่องจากมันเป็นครั้งแรกของนักเรียนที่เห็นว่ามันเสร็จสมบูรณ์
อัตราส่วน 1:27 หมายความว่าในแต่ละครั้งที่เฟืองฟันน้ำนม 36 อันแรกหมุนเต็มหนึ่งรอบเฟืองฟันน้ำนม 12 อันสุดท้าย (อันที่ใกล้กับด้ามจับเอาต์พุตที่สุด) จะหมุน 27 ครั้ง นั่นแสดงให้เห็นว่ามีความได้เปรียบทางกลของความเร็ว
เน้นความได้เปรียบทางกลของความเร็วสำหรับนักเรียนโดยขอให้พวกเขาหมุนด้ามจับด้วย 36 ฟันเฟืองในจังหวะที่เหมาะสมและสังเกตว่าด้ามจับเอาต์พุตหมุนเร็วเพียงใด ตามหลักคณิตศาสตร์ด้ามจับเอาต์พุตจะหมุนเร็วกว่าด้ามจับอินพุต 27 เท่า!
ขั้นตอนที่ 4: การชันสูตรพลิกศพ อัตราส่วนเฟืองผสมของกล่องสำหรับแรงบิด

- สร้างผู้เชี่ยวชาญค้นหาด้านข้างของ M.A.D. กล่องที่ด้ามจับอินพุตหมุนเฟือง 12 ซี่และแสดงให้กลุ่มดู คำแนะนำ: มันเป็นด้านตรงข้ามของ M.A.D. กล่องตามที่คุณใช้ด้านบน ชี้ให้เห็นว่าเมื่อใช้ด้ามจับอินพุตนี้เฟืองขับทั้งหมดเป็นเฟืองฟันน้ำนม 12 เฟืองและเฟืองขับทั้งหมดเป็นเฟืองฟันน้ำนม 36 เฟือง
- เครื่องคิดเลขและเครื่องบันทึกให้กรอกและตรวจสอบสมการด้านล่าง:
- ทีมงานทั้งหมดควรพยายามตอบคำถามต่อไปนี้: อัตราส่วนเกียร์แบบผสมคืออะไรและหมายความว่าอย่างไร ? คุณหมุนด้ามจับด้วยเฟือง 12 ซี่กี่ครั้งเพื่อหมุนด้ามจับอีกอันหนึ่งหนึ่งหนึ่งครั้ง?
- ผู้บันทึกควรจัดระเบียบคำตอบที่ดีที่สุดของทีมและเขียนลงในสมุดบันทึกวิศวกรรม
![]() กล่องเครื่องมือครู
- การ
แก้ปัญหา
กล่องเครื่องมือครู
- การ
แก้ปัญหา
เครื่องคิดเลขและเครื่องบันทึกในกลุ่มควรตระหนักว่าการคำนวณควรเสร็จสมบูรณ์ดังนี้:
-
เศษส่วนที่ขาดหายไปในอัตราส่วนเกียร์หนึ่งคือ 3/1
-
เศษส่วนที่ขาดหายไปในอัตราส่วนเกียร์สองคือ 36/12 และ 3/1
-
เศษส่วนที่ขาดหายไปในอัตราส่วนเกียร์สามคือ 36/12
สมการสำหรับการคำนวณอัตราส่วนเกียร์ของสารประกอบขาดหายไป 3/1 และ 3/1 ซึ่งให้ผลผลิต 27/1 และอัตราส่วนเกียร์ของสารประกอบคือ 27: 1
อัตราส่วน 27: 1 หมายความว่าเฟืองฟันน้ำนม 12 ตัวแรกต้องหมุนครบ 27 รอบเพื่อให้เฟืองฟันน้ำนม 36 ตัวสุดท้าย (ตัวที่อยู่ใกล้กับด้ามจับเอาต์พุตมากที่สุด) หมุนครบหนึ่งรอบ นั่นแสดงให้เห็นว่ามีข้อได้เปรียบทางกลของแรงบิด
เน้นความได้เปรียบทางกลของแรงบิดสำหรับนักเรียนโดยขอให้พวกเขาหมุนด้ามจับด้วยเฟือง 12 ซี่ด้วยความเร็วที่เหมาะสมและรู้สึกถึงแรงของด้ามจับเอาต์พุตขณะหมุน ตามหลักคณิตศาสตร์ด้ามจับเอาต์พุตจะหมุนด้วยแรง 27 รอบของด้ามจับอินพุต!
ขั้นตอนที่ 5: คิดถึงการชันสูตรพลิกศพ การออกแบบกล่อง
ทำไมเอ็ม .เอ .ดี. จึงไม่เป็นเช่นนั้น หกเกียร์ของกล่องทั้งหมดในแถวเดียว?

การออกแบบที่เฟืองทั้งหมดถูกมัดเป็นแนวเรียกว่ารถไฟ เกียร์ ภาพด้านบนแสดงการชันสูตรพลิกศพ เกียร์ของกล่องเป็นขบวนเกียร์
ชุดเกียร์แบบนี้มีอัตราส่วนเกียร์เพียงหนึ่งเดียวและ ไม่ ใช่อัตราส่วนเกียร์แบบผสม อัตราส่วนคือ 1: 3 หรือ 3: 1 ขึ้นอยู่กับว่าเกียร์แรกหรือเกียร์สุดท้ายเป็นเกียร์ขับขี่ เฉพาะขนาดของเฟืองตัวแรกและตัวสุดท้ายในชุดเฟืองนี้มีความสำคัญต่ออัตราส่วนเฟือง
เฟืองระหว่างเฟืองตัวแรกและเฟืองตัวสุดท้ายเรียกว่า เฟืองว่าง พวกเขาไม่ได้เพิ่มพลังหรือความเร็ว เกียร์ว่างจะเปลี่ยนทิศทางของการหมุนเท่านั้น
ทำไมการชันสูตรพลิกศพถึงไม่เป็นเช่นนั้น กล่องที่ออกแบบมาเพียงสองเกียร์: เกียร์ขนาดเล็กและเกียร์ที่มีฟันมากกว่า 27 เท่า?
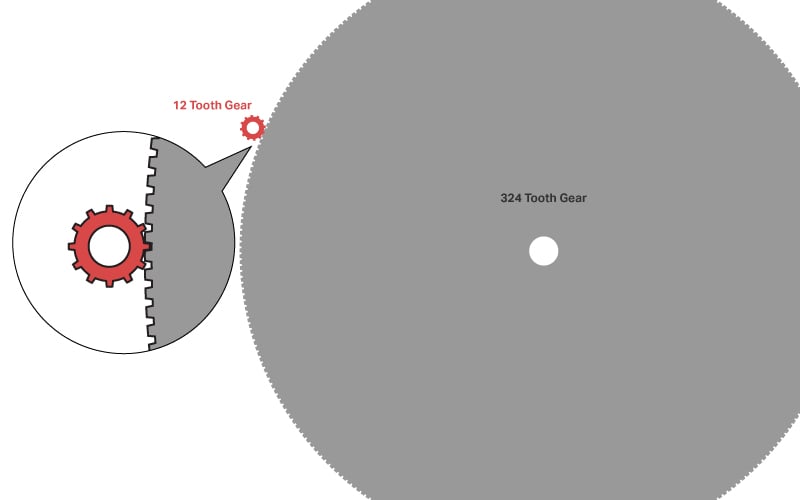
อัตราส่วนเกียร์ของสารประกอบของ M.A.D. Box คือ 1:27 หรือ 27: 1 คุณอาจสงสัยว่าทำไมมันไม่ได้รับการออกแบบด้วยเฟืองเพียงสองตัว: เฟืองฟันน้ำนม 12 ตัวและเฟืองฟันน้ำนม 324 ตัว นั่นจะนำไปสู่อัตราทดเกียร์ 1:27 หรือ 27: 1
มีเหตุผลสองประการที่ M.A.D. กล่องไม่ได้ออกแบบด้วยเฟืองฟัน 324
เหตุผลแรกคือไม่มีฟันเฟืองพลาสติก 324 ของ vex เกียร์ที่ใหญ่ที่สุดในชุดคือ 60 ฟันเฟือง เมื่อวิศวกรออกแบบสร้างพวกเขาต้องคำนึงถึงวัสดุที่มีอยู่และไม่มีอุปกรณ์ฟัน 324
เหตุผลที่สองคือเฟืองฟัน 324 ถ้ามีจะมีขนาดใหญ่มาก เกียร์ที่มีขนาดใหญ่จะทำให้การสร้างยากต่อการจัดการ อัตราส่วนเกียร์ของสารประกอบเหมาะสมกว่าสำหรับการออกแบบอุปกรณ์มือถือ เมื่อวิศวกรออกแบบสร้างพวกเขาต้องคำนึงถึงวิธีที่ผู้บริโภคจะใช้อุปกรณ์
![]() สร้างแรงจูงใจในการอภิปราย
-
สรุป
สร้างแรงจูงใจในการอภิปราย
-
สรุป
นักเรียนควรจบห้องปฏิบัติการ STEM นี้ด้วยความเข้าใจว่าอัตราส่วนเกียร์มีความสำคัญต่อการออกแบบหุ่นยนต์อย่างไร โดยสรุปอัตราส่วนเกียร์ที่กำหนดถูกใช้เพื่อถ่ายโอนกำลังหรือเพื่อสร้างแรงบิดหรือความเร็วข้อได้เปรียบเชิงกลสำหรับชิ้นส่วนของหุ่นยนต์ เริ่มต้นด้วยการสนทนานี้:
ถาม: เพื่อให้ได้ความได้เปรียบทางกลของความเร็วซึ่งมีขนาดใหญ่กว่า: เกียร์ขับขี่หรือเกียร์ขับเคลื่อน
ตอบ : เกียร์ขับขี่มีขนาดใหญ่กว่าเกียร์ขับเคลื่อนเมื่อสร้างความเร็ว
ถาม: เหตุใดคุณจึงต้องการเพิ่มความเร็วของหุ่นยนต์
ตอบ: หุ่นยนต์สามารถเคลื่อนที่และทำงานได้เร็วที่สุดเท่าที่จะเป็นไปได้
ถาม: เหตุใดคุณจึงต้องการเพิ่มแรงบิดให้กับหุ่นยนต์ คำแนะนำ: พิจารณาชิ้นส่วนที่เคลื่อนไหว
ตอบ: หุ่นยนต์อาจมีน้ำหนักมากหรือต้องเคลื่อนย้ายวัตถุที่มีน้ำหนักมาก การเพิ่มขึ้นของแรงบิดบนระบบขับเคลื่อน (ฐานล้อ) จะช่วยให้มันเคลื่อนที่ได้ การเพิ่มขึ้นของแรงบิดของกรงเล็บหรือแขนของมันสามารถช่วยในการยกของหนักได้
ถาม: เหตุใดคุณจึงอาจใช้อัตราส่วนเกียร์ผสมแทนที่จะใช้เกียร์สองที่มีความแตกต่างกันมากขึ้นในจำนวนฟัน
ตอบ: อัตราทดเกียร์ บางรุ่นมีขนาดใหญ่มากจนโครงสร้างไม่สามารถมีเกียร์ขนาดดังกล่าวได้ อาจไม่มีเกียร์ที่มีขนาดเท่าที่จำเป็นในการสร้างอัตราทดเกียร์นั้น ดังนั้นอัตราส่วนเกียร์ผสมจึงช่วยให้วิศวกรสร้างข้อได้เปรียบทางกลมากขึ้นในขณะที่ลดพื้นที่ที่ต้องการ
ถาม: เหตุใดคุณจึงอาจรวมรถไฟเกียร์ไว้ในบิลด์ด้วย? มันเพิ่มแรงบิดหรือความเร็วหรือไม่?
ตอบ: รถไฟเกียร์ช่วยในการถ่ายโอนกำลังแต่ไม่เพิ่มแรงบิดหรือความเร็วมากกว่าอัตราส่วนระหว่างเฟืองท้ายและเฟืองท้ายบนรถไฟ
นักเรียนจะกลับไปคิดเกี่ยวกับเรื่องนี้ในหน้าใช้งานเกี่ยวกับการออกแบบหุ่นยนต์การแข่งขันสำหรับแรงบิดหรือความเร็ว สำหรับการอ่านเพิ่มเติมมีบทความในไลบรารี vex เกี่ยวกับ วิธีการใช้อัตราส่วนเกียร์อย่างง่าย บทความนี้เขียนขึ้นภายใต้บริบทของหุ่นยนต์ vex V5 แต่แนวคิดนี้นำไปใช้กับการออกแบบหุ่นยนต์ vex IQ เช่นกัน