In den vorherigen Lektionen haben Sie gelernt, wie man ein Dreieck zeichnet, indem man fehlende Koordinaten findet. In dieser Lektion erfahren Sie, was zu tun ist, wenn sich der 6-Achsen-Arm entlang der x- oder y-Achse in die negative Richtung bewegt, und wie Sie fehlende Koordinaten berechnen.
Am Ende dieser Lektion zeichnen Sie einen Diamanten, indem Sie die von Ihnen bestimmten Koordinaten miteinander verbinden.
Fehlende Koordinaten finden
In Lektion 3 haben Sie die fehlenden Koordinaten eines Dreiecks bestimmt, indem Sie einen Punkt des Dreiecks und zwei Seitenlängen kennen. Sie werden nun auf diesem Projekt aufbauen, um ein zweites Dreieck zu zeichnen.
Finding Point D
Zeichnen Sie die bekannten Informationen in Ihrem technischen Notizbuch.
Das Dreieck ABC befindet sich an folgenden Punkten:
- A (125, 125, 0)
- B (175, 125, 0)
- C (125, 175, 0)
Das war das Dreieck, das du in Lektion 3 gezeichnet hast.
Das zweite Dreieck, ADE, hat Seitenlängen von 50 mm, für die Seiten AD und AE. Die Seiten des Dreiecks ADE sind in diesem Bild mit blauen Linien und Text dargestellt.
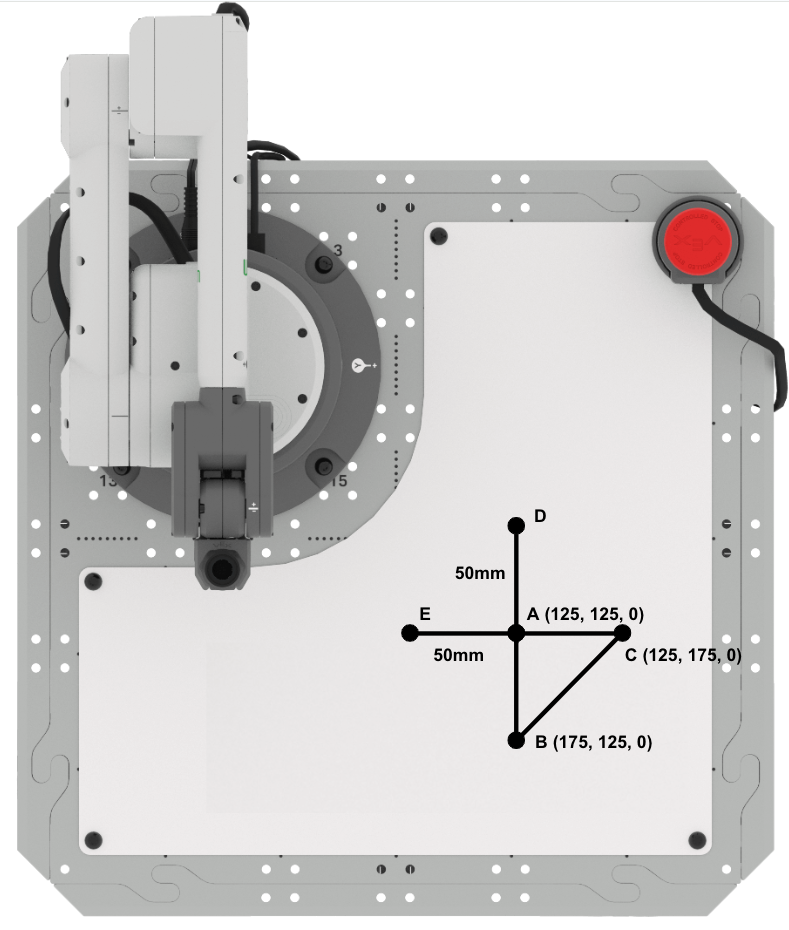
Seite AD des rechtwinkligen Dreiecks ADE, ist parallel zur x-Achse.
Beachten Sie, dass die x-Koordinaten bei der Bewegung von Punkt A zu Punkt D entlang der x-Achse niedriger werden. Dies wird sich in der Gleichung widerspiegeln, die zur Berechnung der x-Koordinate des Punktes D verwendet wird.
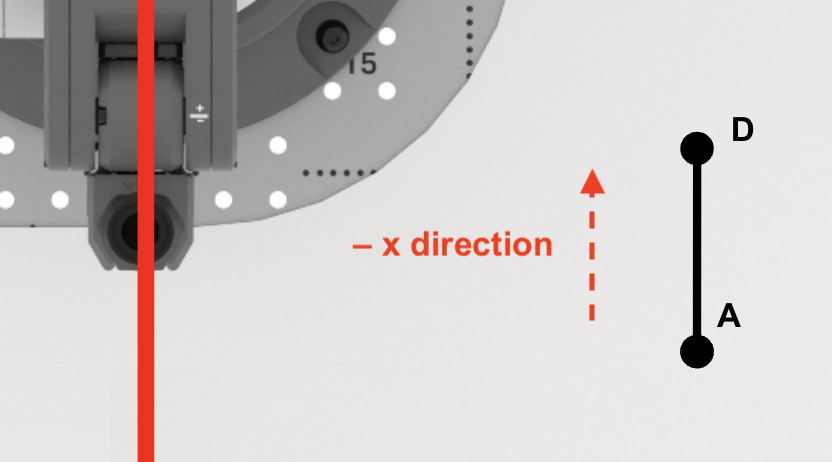
Finde die x-Koordinate von Punkt D.
Da sich der 6-Achsen-Arm entlang der x-Achse in die negative Richtung bewegt, müssen Sie die Subtraktion verwenden. Subtrahieren Sie die Länge von AD von der x-Koordinate von Punkt A, um die x-Koordinate von Punkt D zu finden.
Die x-Koordinate von Punkt D beträgt 75 mm. Notieren Sie dies in Ihrem technischen Notizbuch.

Als nächstes finden wir die y-Koordinate von Punkt D.
Da die Punkte A, B und D entlang der Linie y=125 mm liegen, ist die y-Koordinate des Punktes D die gleiche wie die Punkte A und B (125 mm). Notieren Sie dies in Ihrem technischen Notizbuch.
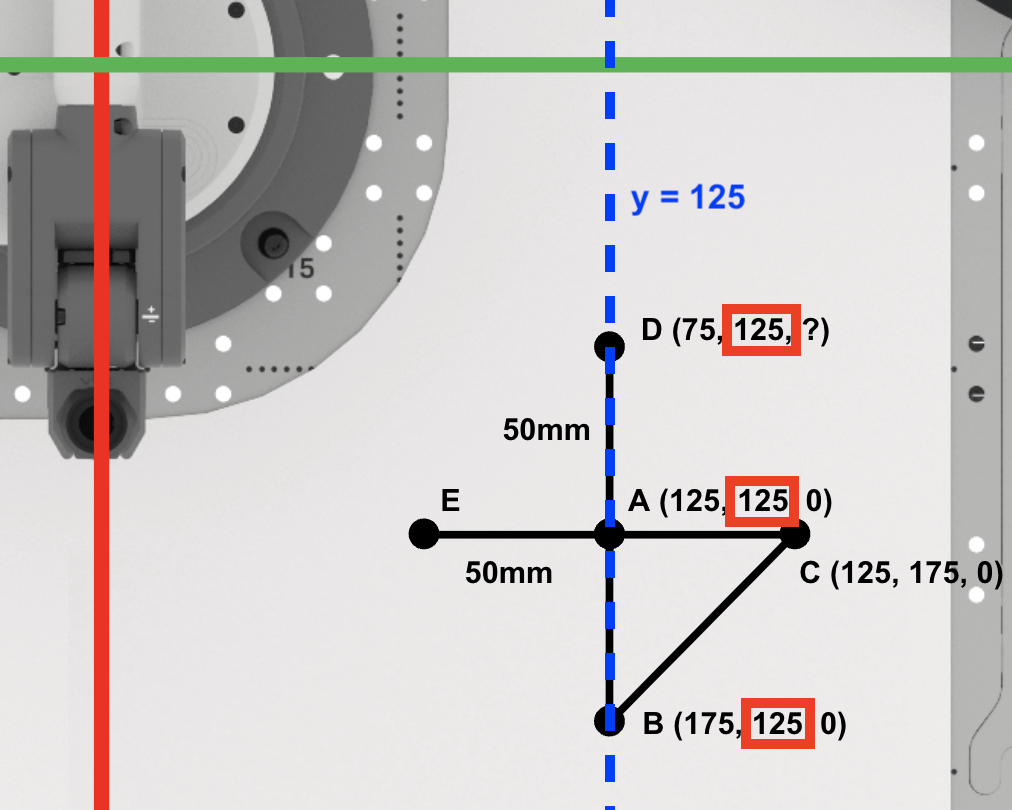
Da sich der Stift nicht zwischen den Punkten A und D hebt, bleibt die z-Koordinate von Punkt D Null.
Punkt D ist (75, 125, 0). Notieren Sie dies in Ihrem technischen Notizbuch.
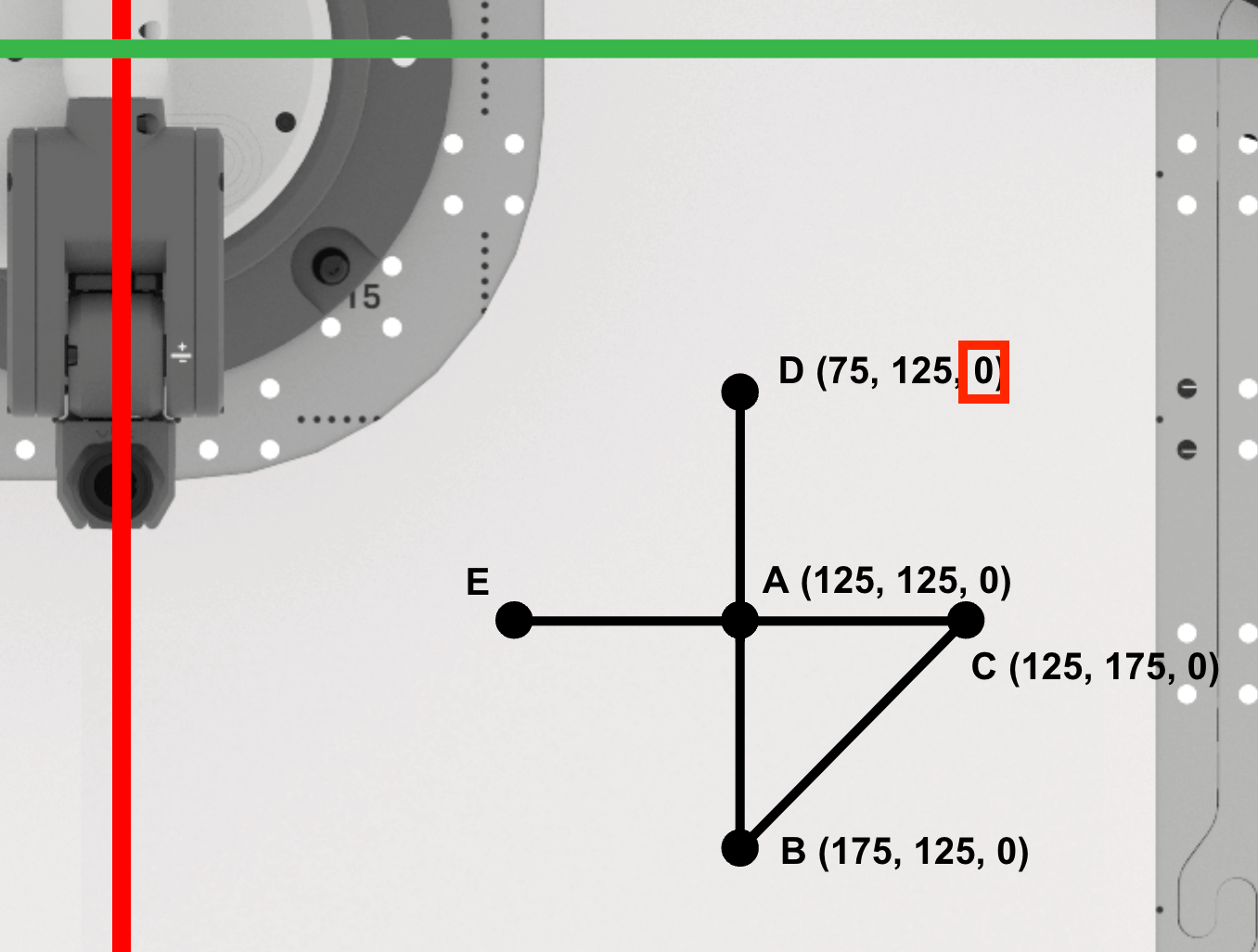
Befundpunkt E
Finde die x-Koordinate von Punkt E.
Da die Punkte A, C und E entlang der Linie x=125 mm liegen, ist der x-Wert des Punktes E der gleiche wie die Punkte A und C (125 mm).
Notieren Sie dies in Ihrem technischen Notizbuch.
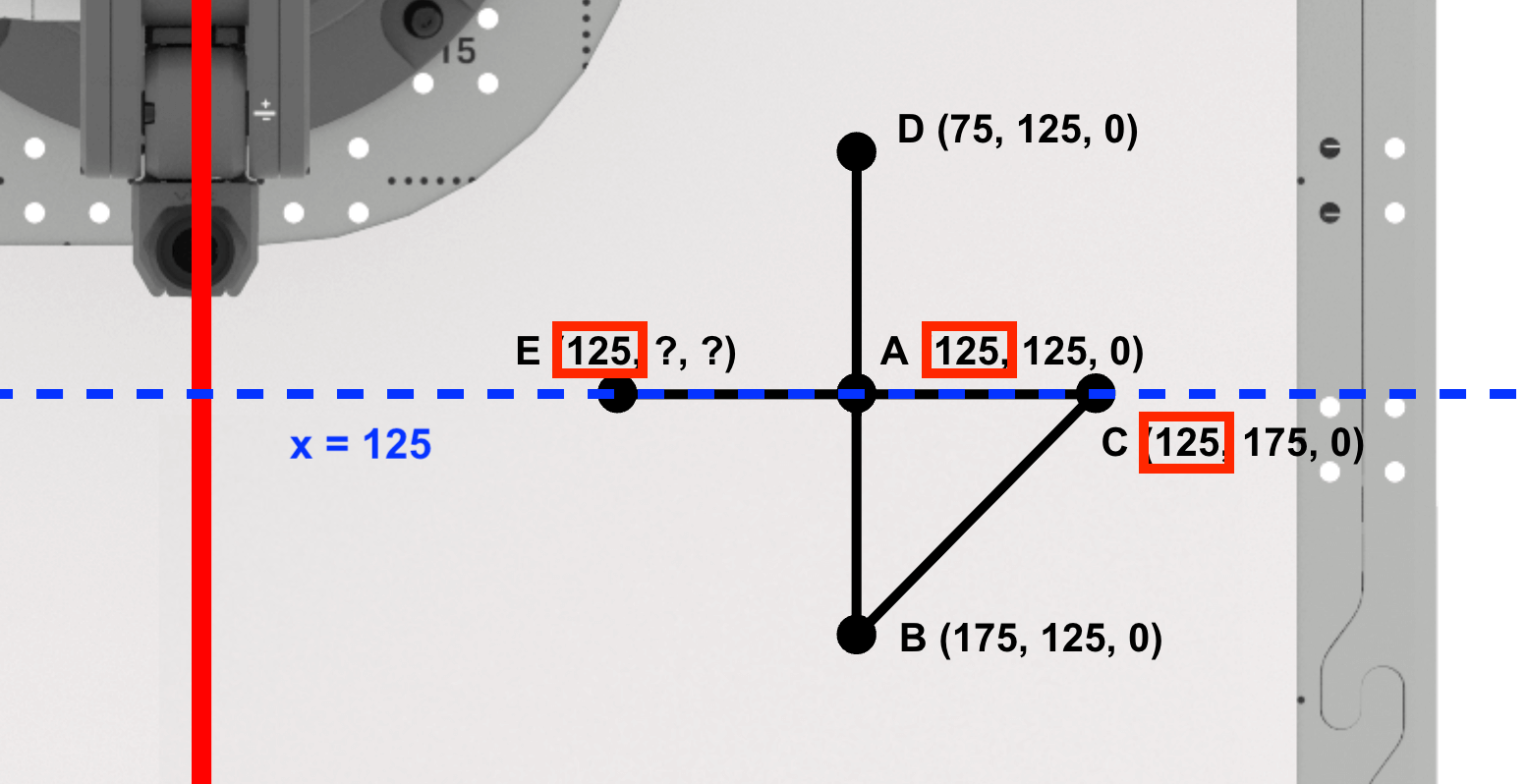
Die Seite AE des rechten Dreiecks ADE ist parallel zur y-Achse.
Beachten Sie, dass die y-Koordinaten niedriger werden, wenn Sie sich entlang der y-Achse von Punkt A zu Punkt E bewegen. Dies wird sich in der Gleichung widerspiegeln, die zur Berechnung der y-Koordinate des Punktes E verwendet wird.

Suchen Sie als Nächstes die y-Koordinate von Punkt E.
Da sich der 6-Achsen-Arm entlang der y-Achse in die negative Richtung bewegt, müssen Sie die Subtraktion verwenden. Subtrahiere die Länge von AE von der y-Koordinate von Punkt A, um die y-Koordinate von Punkt E zu finden.
Die y-Koordinate des Punktes E beträgt 75 mm. Notieren Sie dies in Ihrem technischen Notizbuch.
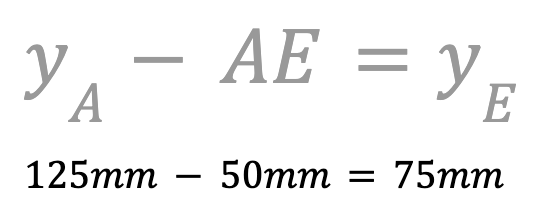
Da sich der Stift nicht zwischen den Punkten D und E hebt, bleibt die z-Koordinate des Punktes E Null.
Punkt E ist (125, 75, 0). Notieren Sie dies in Ihrem technischen Notizbuch.
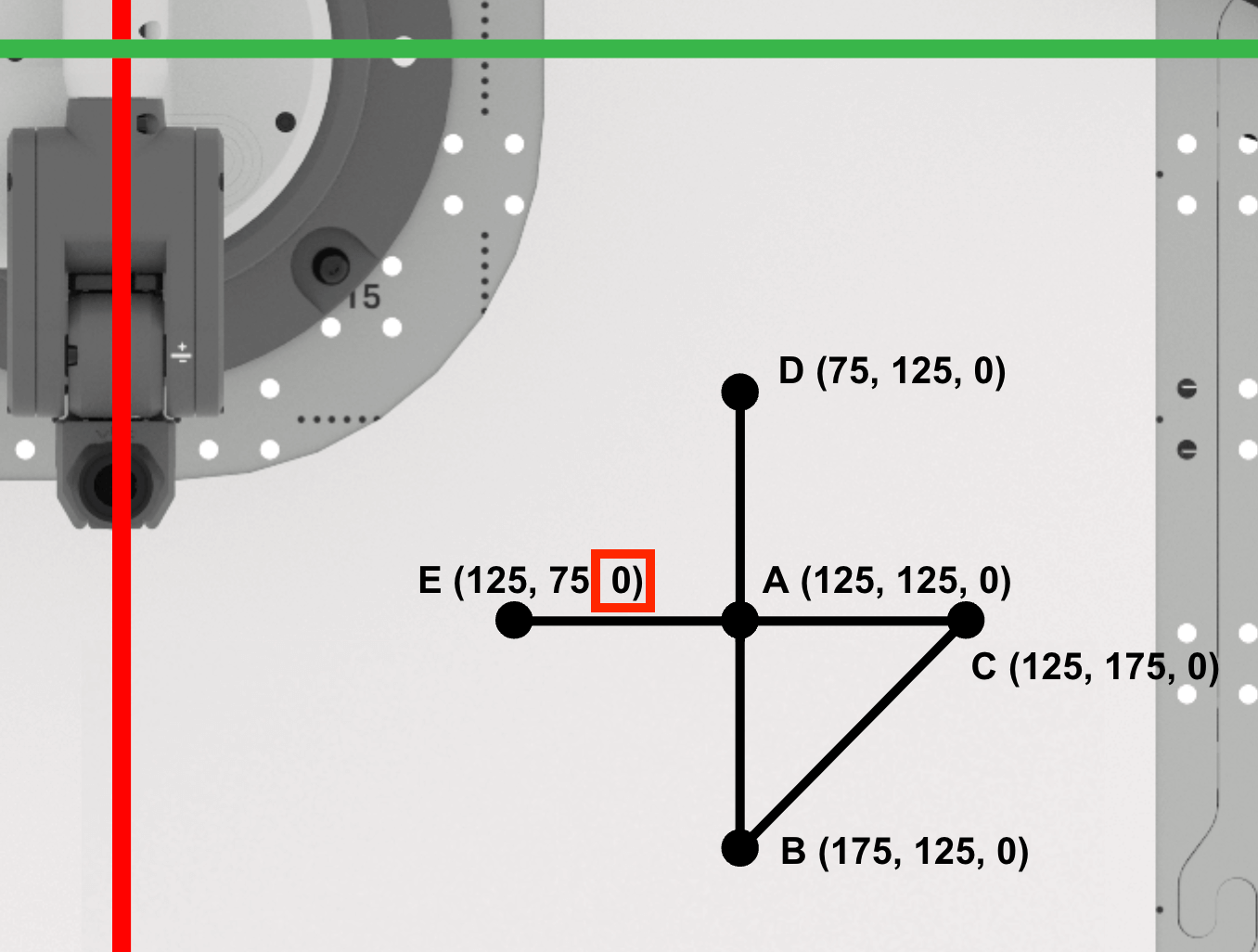
Codierung des 6-Achsen-Arms zum Zeichnen des Dreiecks ADE
Nachdem Sie nun die Koordinaten für die Punkte D und E bestimmt haben, ist es an der Zeit, ein VEXcode EXP-PROJEKT für den 6-Achsen-Arm zu erstellen, um die Punkte A, D und E zu verbinden, um ein weiteres Dreieck zu zeichnen.
Öffnen Sie das Projekt Einheit 5 Lektion 3, um das Dreieck ABC auf dem Whiteboard zu zeichnen, oder erstellen Sie das Projekt wie hier gezeigt neu.

Ändern Sie den hier angezeigten Kommentarblock in "Gehen Sie zu Punkt A, um das erste Dreieck zu starten."
Da Sie zwei Dreiecke zeichnen, kann der Kommentar geändert werden, um Kontext darüber bereitzustellen, welche Blöcke im Projekt verwendet werden, um das erste Dreieck im Vergleich zum zweiten Dreieck zu zeichnen.
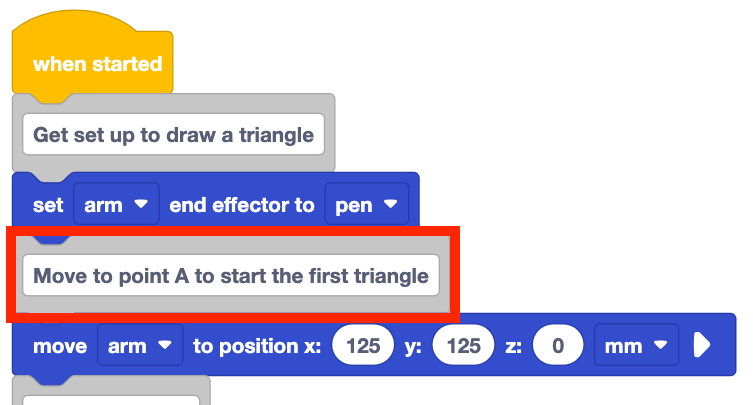
Fügen Sie einen Kommentarblock am unteren Rand des Stapels hinzu und geben Sie "Zu Punkt D bewegen, um das zweite Dreieck zu starten" ein.
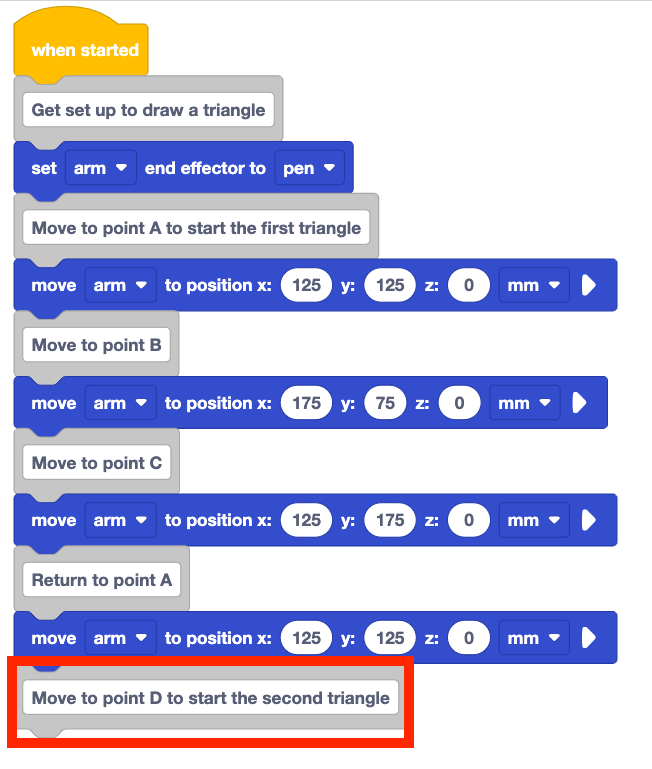
Fügen Sie dem Stapel unter dem Kommentarblock einen Verschieben-zu-Position-Block hinzu.
Legen Sie die Parameter des Bewegungsblocks auf die Koordinaten von Punkt D fest, die in Ihrem technischen Notizbuch dokumentiert sind.

Fügen Sie Kommentarblöcke hinzu und verschieben Sie die Blöcke für Punkt E und die Rückkehr zu Punkt A, um das zweite Dreieck zu vervollständigen.
Legen Sie die Parameter der Blöcke zum Positionieren bewegen auf die Koordinaten der Punkte E und A fest, die in Ihrem technischen Notizbuch aufgezeichnet wurden.
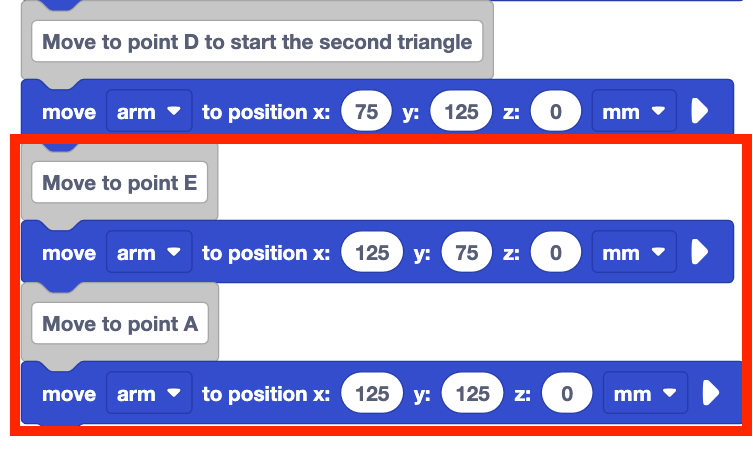
Achten Sie darauf, Ihr Projekt umzubenennen und auf Ihrem Gerät zu speichern.

Ihr gesamtes Projekt sollte nach Abschluss so aussehen.
Wenn Sie mit dem Erstellen Ihres Projekts fertig sind, stellen Sie sicher, dass der 6-Achsen-Arm mit VEXcode EXP verbunden ist, und führen Sie das Projekt aus.

Beenden Sie das Projekt, wenn der 6-Achsen-Arm mit dem Zeichnen der beiden Dreiecke fertig ist.
Der 6-Achsen-Arm zeichnet das Dreieck ABC wie in Lektion 3. Dann bewegt es sich zu Punkt D, um die erste Seite des Dreiecks ADE zu zeichnen. Dann bewegt sich der 6-Achsen-Arm von Punkt D zu Punkt E, um die zweite Seite des Dreiecks ADE zu vervollständigen, und beendet das Dreieck, indem er die Packung zu Punkt A bewegt.
Hinweis: Dieses Bild zeigt, dass der 6-Achsen-Arm manuell bewegt wurde, nachdem das Projekt gestoppt wurde, so dass beide Dreiecke deutlich zu sehen sind.

Aktivität
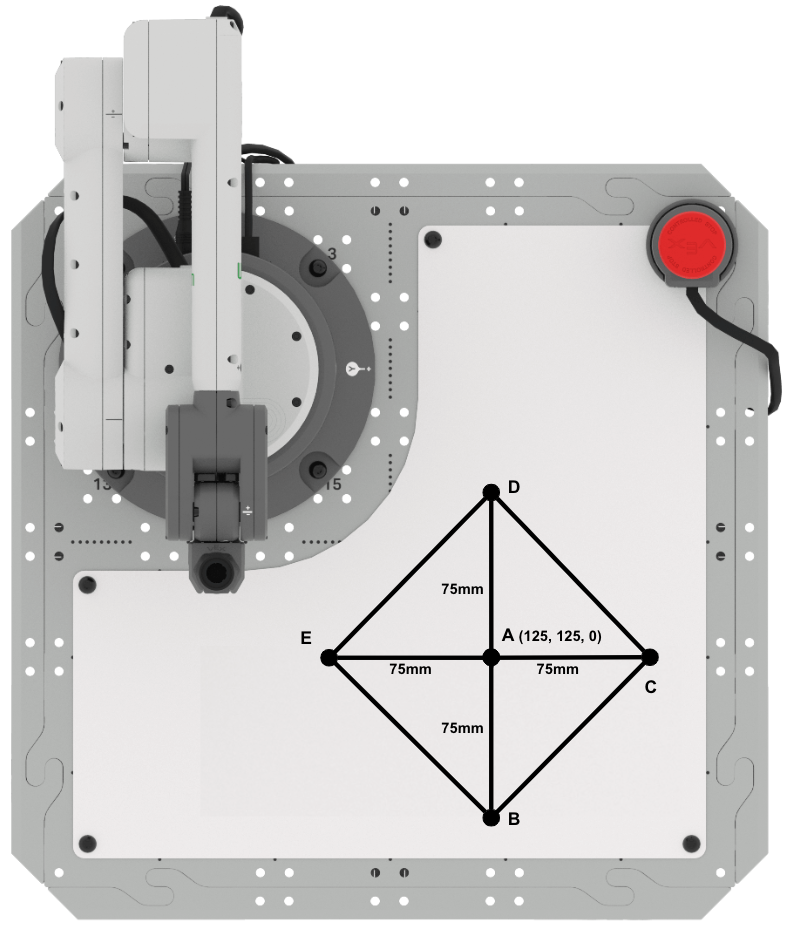
In dieser Lektion haben Sie gelernt, Dreiecke mit Seiten zu zeichnen, die eine Bewegung in die negative Richtung entlang der Achsen erfordern. Jetzt werden Sie Ihr Lernen anwenden, um einen Diamanten zu zeichnen, der aus vier Dreiecken besteht.

- Setup: Zeichnen Sie die Punkte A, B, C, D und E in Ihrem
technischen Notizbuch wie oben gezeigt.
- Punkt A befindet sich bei (125, 125, 0)
- Die Seitenlängen AB, AC, AD und AE betragen 75 mm
- Aktivität:
- Verwenden Sie die Formeln aus Lektionen 3 und 4, um die Koordinaten der obigen Punkte B, C, D und E zu bestimmen. Notieren Sie die Koordinaten in Ihrem technischen Notizbuch.
- Erstellen Sie ein VEXcode EXP-PROJEKT, um die Punkte zu verbinden und die
oben
gezeigte Form zu zeichnen.
- Sie können auf dem Lektion 4-Projekt aufbauen oder das Signal Tower-Vorlagenprojekt herunterladen.
- Stellen Sie sicher, dass Sie den Endeffektorblock auf Stift setzen , um loszulegen.
- Verwenden Sie Kommentare, um das Verhalten des 6-Achsen-Arms in Ihrem Projekt zu kommunizieren.
- Wenn Sie mit dem Erstellen Ihres Projekts fertig sind, führen Sie das Projekt aus, um es zu testen.
- Hat Ihr Projekt den oben gezeigten Diamanten gezeichnet? Wenn nicht, ändern Sie Ihr Projekt weiter und testen Sie es, bis Sie erfolgreich sind.
- Nachdem Sie das Projekt abgeschlossen haben, benennen Sie es um und speichern Sie es auf Ihrem Gerät.
Überprüfe dein Verständnis
Bevor Sie mit der nächsten Lektion fortfahren, stellen Sie sicher, dass Sie die Konzepte in dieser Lektion verstehen, indem Sie die Fragen im folgenden Dokument in Ihrem technischen Notizbuch beantworten.
Fragen zum Verständnis prüfen > (Google Doc / .docx / .pdf)
Wählen Sie Weiter > , um die Putting It All Together -Aktivität abzuschließen.