VEX CTE - Unit 5 - Coding Shapes - Lesson 3: Finding Missing Coordinates

In the previous Lessons, you learned how to draw a triangle on the Whiteboard with the Pen Holder Tool where all the points of the triangle were given. However, if some points of the triangle are not given, they will need to be determined mathematically in order for the 6-Axis Arm to move in multiple axes.

In this Lesson, you will find two missing coordinates of a triangle in order to draw the triangle. At the end of this Lesson, you will apply what you have learned to build onto the triangle to draw a square.

A top down view of the 6-Axis Robotic Arm over a whiteboard with the Pen Holder tool. 4 coordinates labeled A through D form a square shape on the whiteboard.

Finding Missing Coordinates

The 6-Axis Arm is going to draw a triangle. Here is the information we know about this triangle:

Point A is (125, 125, 0).
Each side length is 50mm.
Triangle ABC is a right triangle (a triangle with one 90 º angle).
- The side opposite this angle is the longest side, known as the hypotenuse. The other two sides are called the legs.

Using this information, we can find the two endpoints (points B and C) to draw the triangle.

Follow along with the steps below to find points B and C and draw the triangle.

Finding Point B

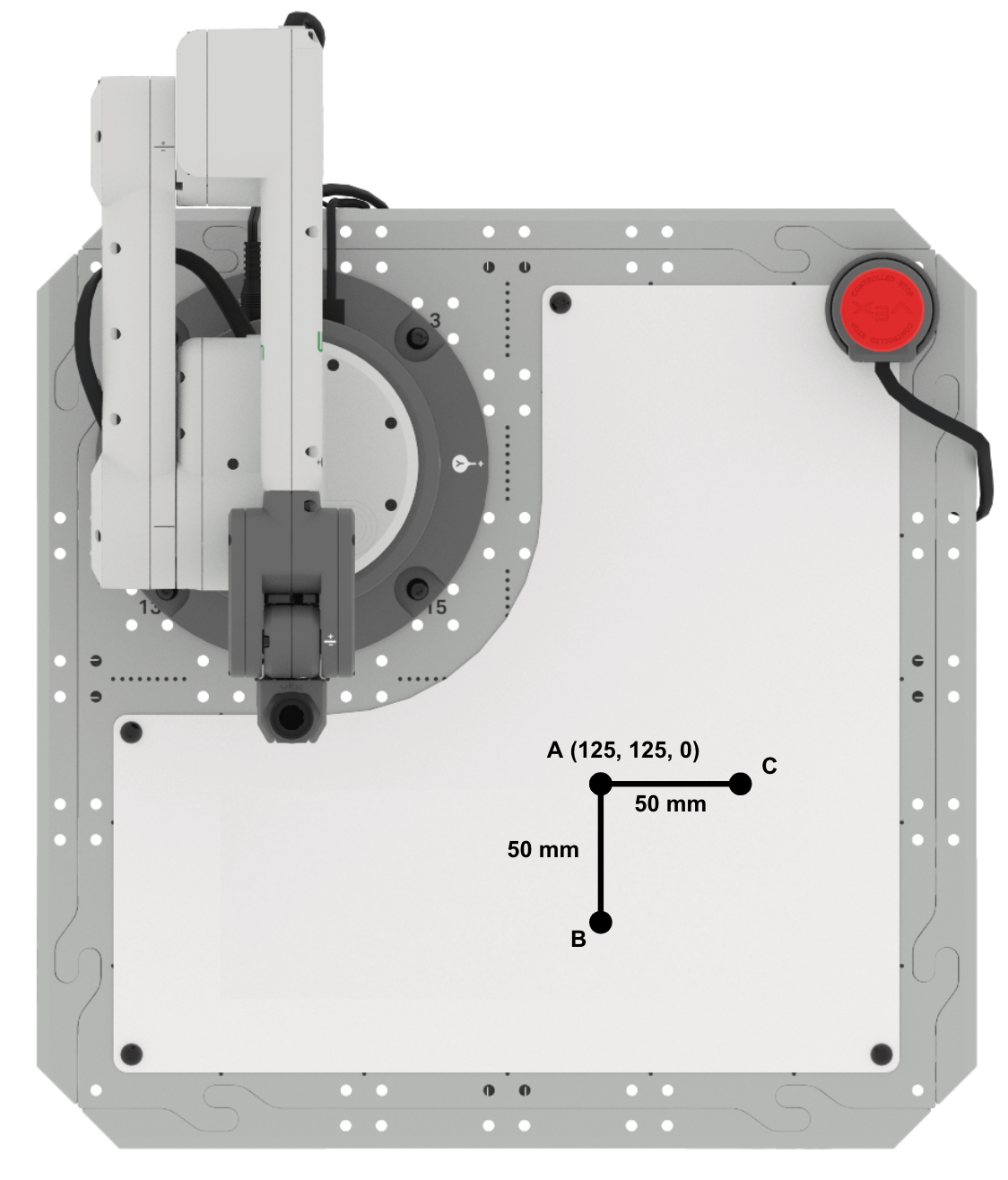
Sketch the known information about the triangle in your engineering notebook.

Point A is located at approximately (125, 125, 0).

The distance from point A to point B is approximately 50mm. The distance from point A to point C is approximately 50mm. Each of these distances corresponds to the side lengths of the triangle.

A top down view of the 6-Axis Robotic Arm over a whiteboard with the Pen Holder tool. 3 coordinates are labeled A through C. Coordinate A is labeled (125, 125, 0) with 50 mm labeling the distances between coordinates A and C and A and B.

Determine the x-coordinate of point B. This can be done by adding the length of AB to the x-coordinate of point A to find the x-coordinate of point B.

The x-value of point B is 175mm. Record this in your engineering notebook.

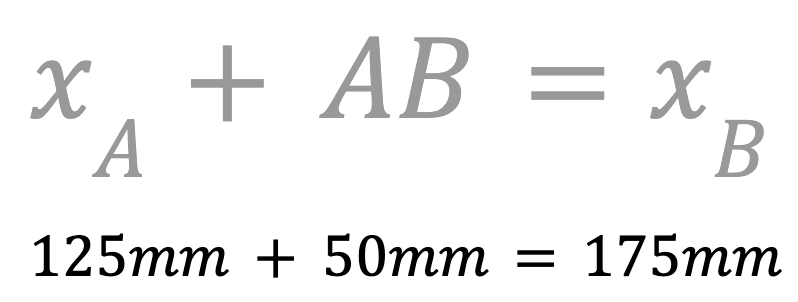
The formula for finding the x coordinate of B reads X of A + AB = x of B. Beneath the formula reads 125mm + 50mm = 175mm.

Next, we will find the y-coordinate of point B.

Since points A and B are along the line y=125mm, the y-coordinate of point B is the same as point A (125mm). Record this in your engineering notebook.

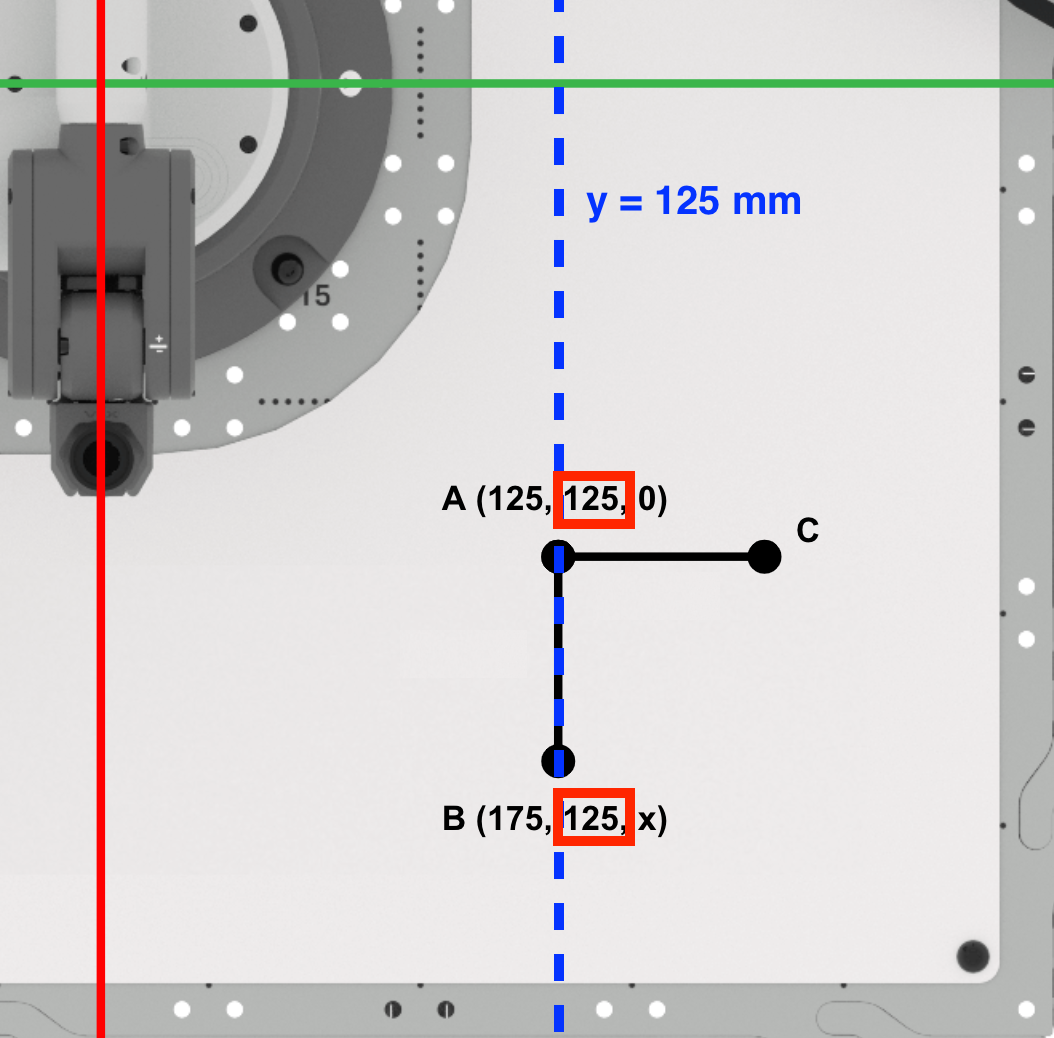
A top down view of the 6-Axis Robotic Arm and tile, showing a grid with the X and Y axes labeled. The A coordinate from before is labeled (125, 125, 0) with the B coordinate below it labeled (175, 125, x). A blue line from the Y's grid line goes through both coordinates and is labeled y = 125 mm. Both y coordinates of A and B are highlighted with a red box.

Since the Pen is not raising between points A and B, the z-coordinate of point B will remain zero.

Point B is (175, 125, 0). Record this in your engineering notebook.

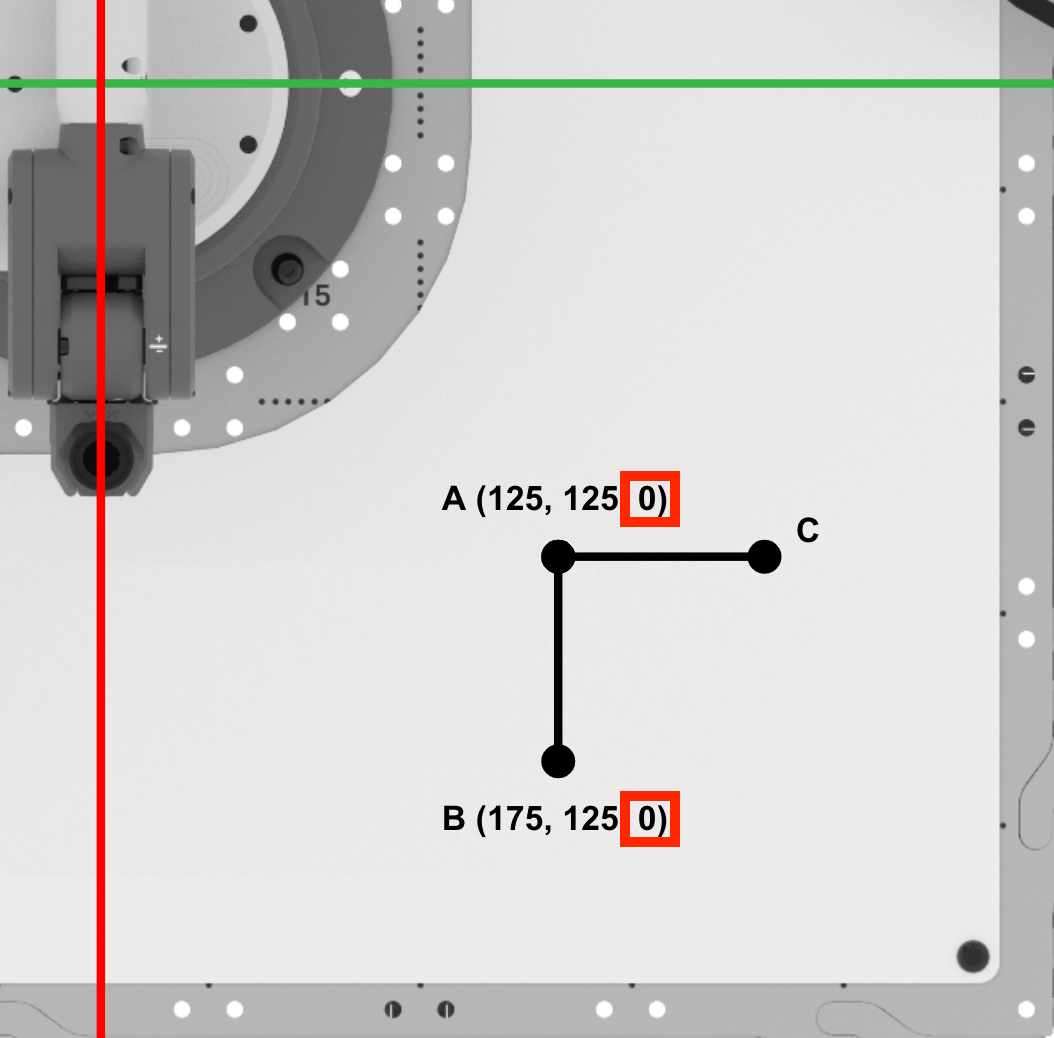
Finding Point C

Find the x-coordinate of point C.

Since points A and C are along the line x=125mm, the x-value of point C is the same as point A (125mm).

Record this in your engineering notebook.

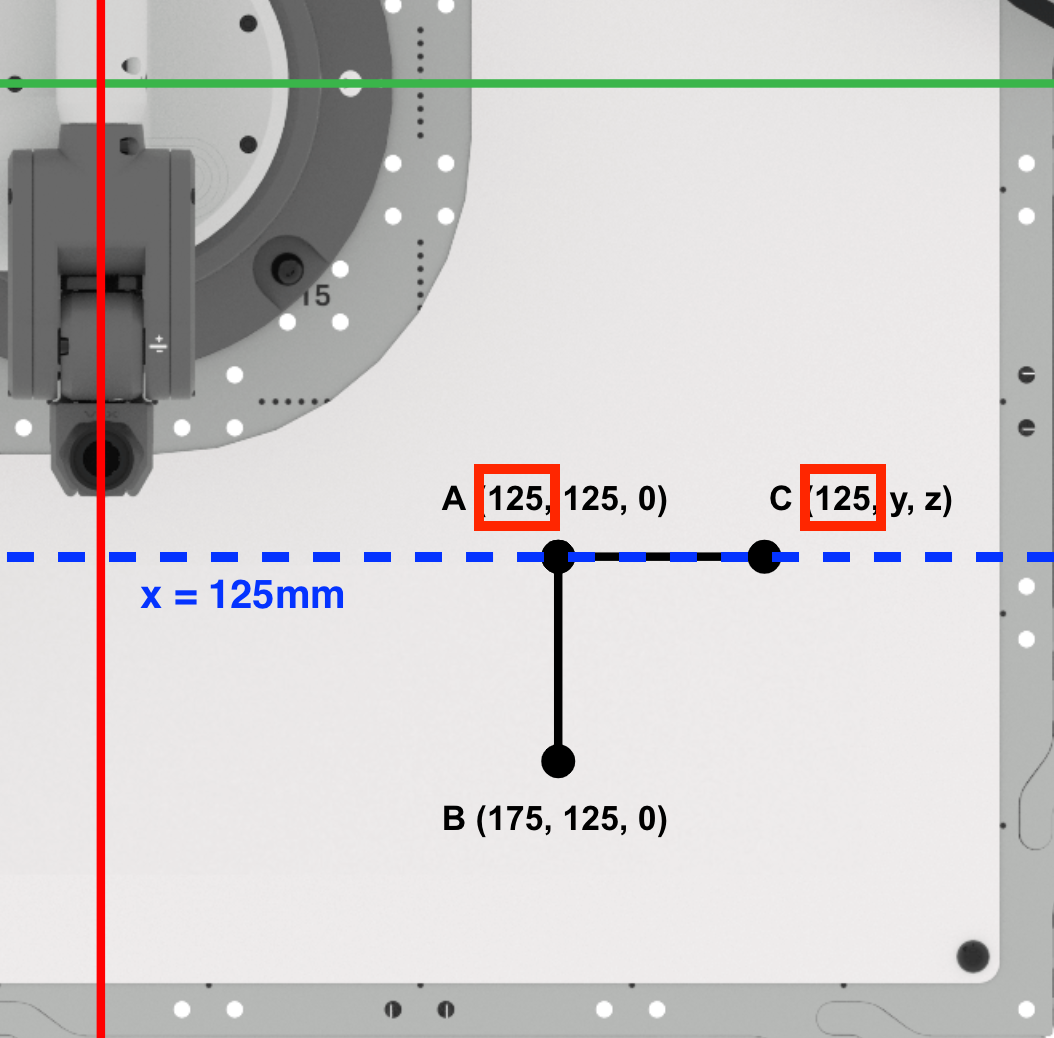
Next, find the y-coordinate of point C.

Since we are drawing a right triangle, we know that side AC will be parallel to the y-axis. Add the length of AC to the y-coordinate of point A to find the y-coordinate of point C.

The y-coordinate of point C is 175mm. Record this in your engineering notebook.

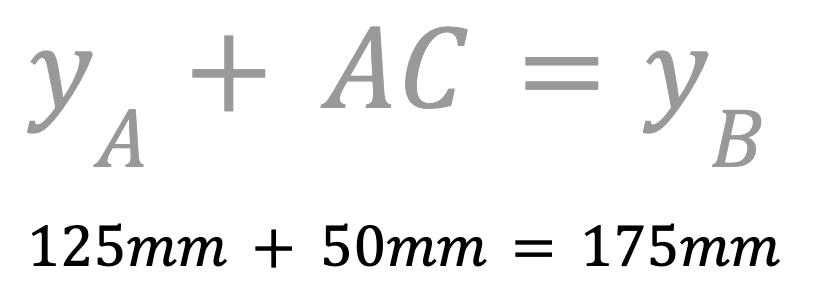
A formula to calculate the y-value of point C reading y underscript A + AC = y underscript B. Below that reads 125 mm + 50 mm = 175 mm.

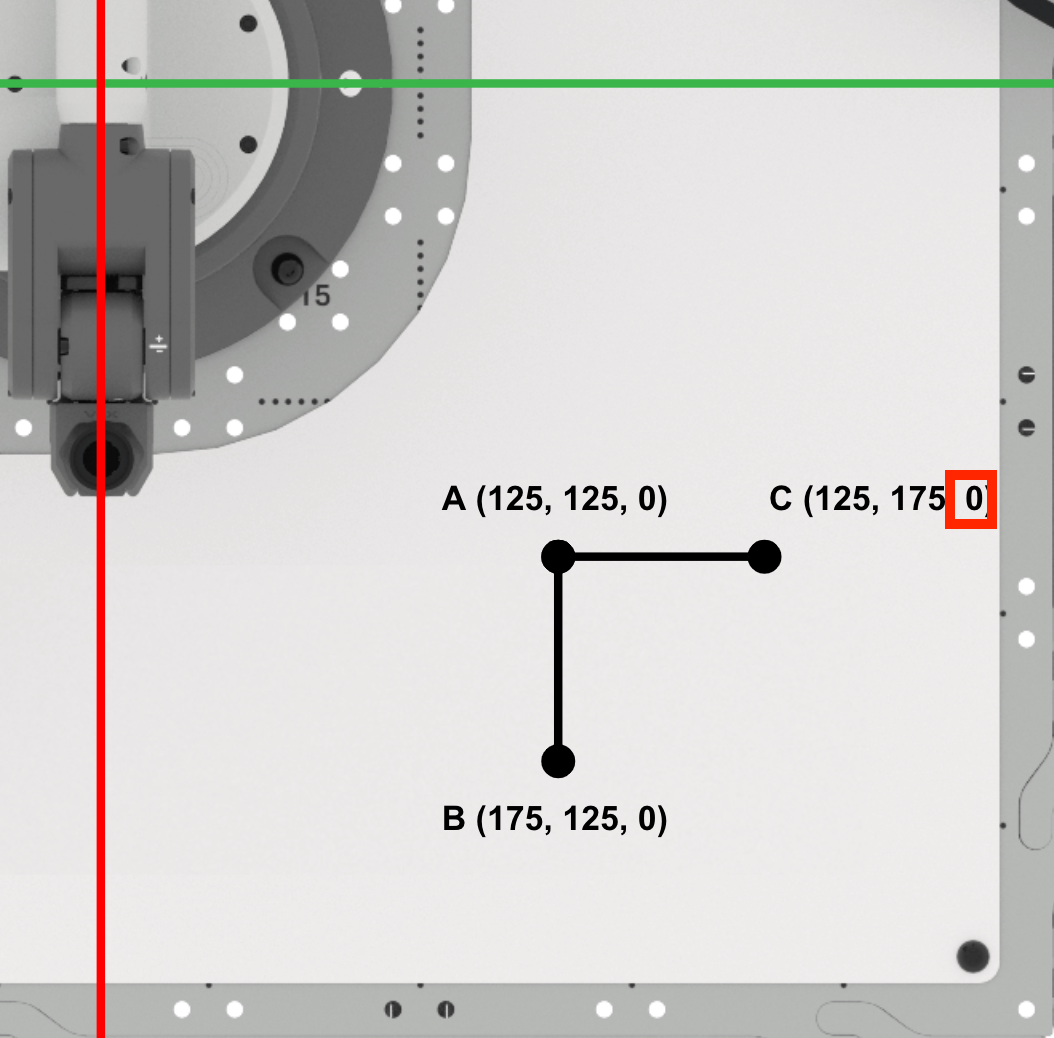
Since the Pen is not raising between points A and C, the z-coordinate of point C will remain zero.

Point C is (125, 175, 0). Record this in your engineering notebook.

Coding the 6-Axis Arm to Connect Points A, B and C

Now that you have determined the coordinates for points B and C, it is time to create a VEXcode EXP project for the 6-Axis Arm to connect points A, B and C in order to draw a triangle.

Open a New Blocks Project by following the steps in this video. In the video clip, File is selected in the Toolbar, and then New Block Project is selected. A dialog box pops up with two options, EXP Brain on the left, and Arm on the right. The Arm option is selected, and a new project opens in the Workspace.

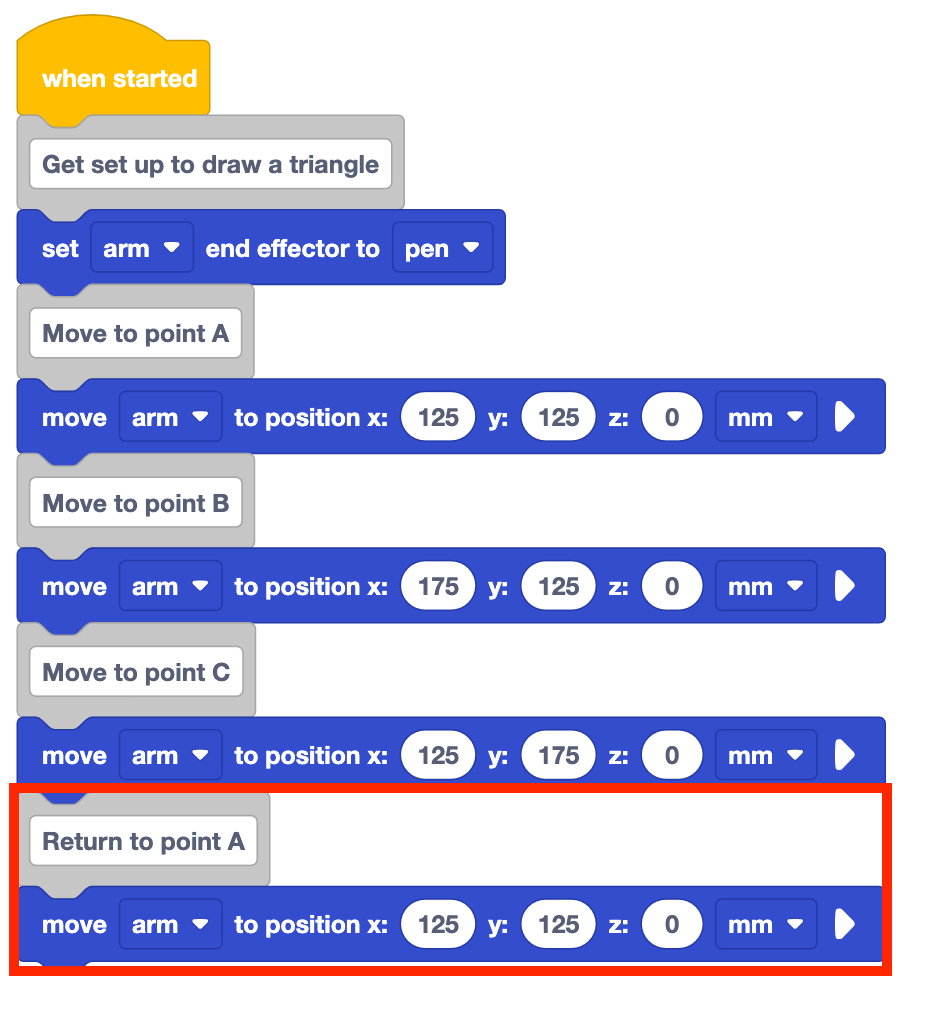
Add a Comment block to the stack and type in 'Get set up to draw a triangle.'

A stack of blocks that starts with a when started block. A comment block is the next block that reads Get set up to draw a triangle and is highlighted with a red box.

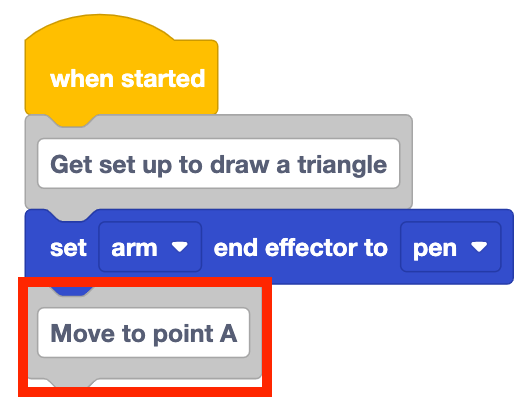
Add a Set end effector block to the stack and set it to 'pen.'

The stack of blocks from before with a set arm end effector to pen block added to the bottom. The second parameter of the block is expanded, showing magnet and pen, with pen selected. This bottom block is highlighted with a red box.

Add a Comment block to the stack and type in 'Move to point A.'

The stack of blocks from before with a comment block reading Move to point A that is highlighted with a red box.

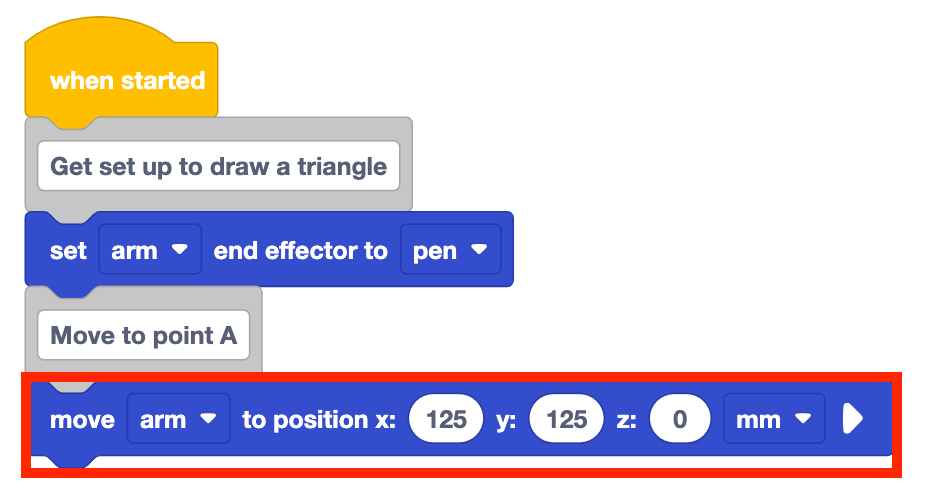
Add a Move to position block to the stack underneath the Comment block.

Set the Move to position block's parameters to point A's coordinates, documented in your engineering notebook.

The stack of blocks from before with a move arm to position x 125 y 125 z 0 mm added to the bottom. This bottom block is highlighted with a red box.

Add Comment and Move to position blocks for points B and C.

Set the parameters of the Move to position blocks to the coordinates of points B and C, that were recorded in your engineering notebook.

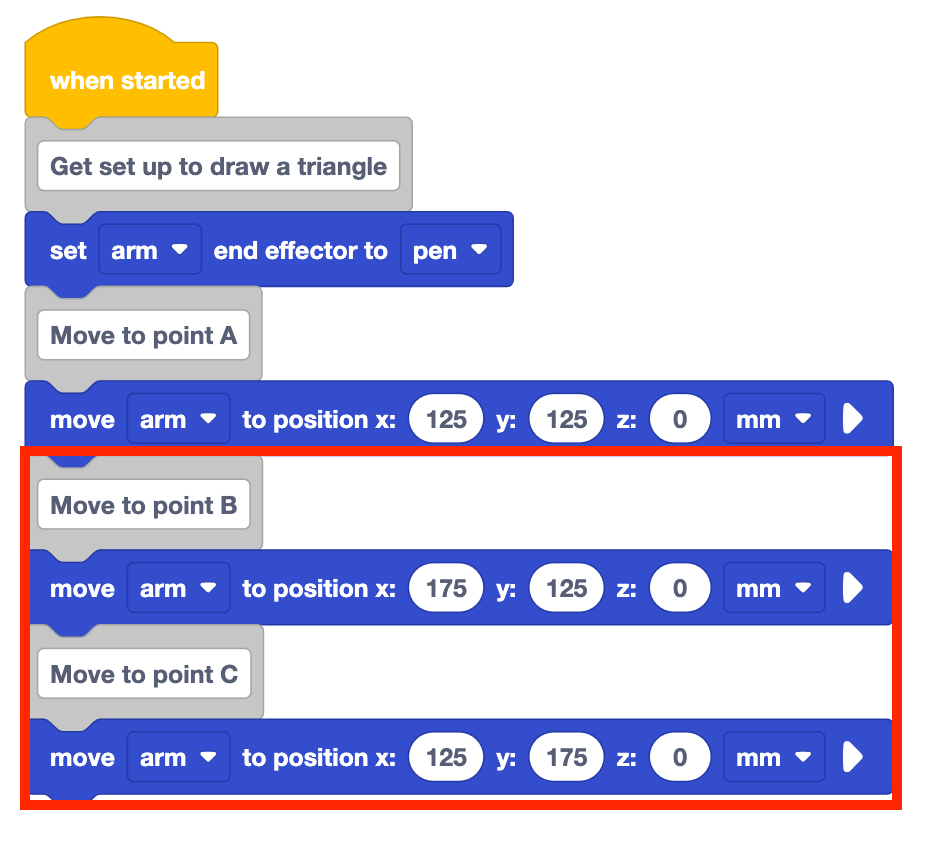
The stack of blocks from before with four new blocks added to the bottom in this order, a comment block reading move to point B, a move arm to position x 175 y 125 z 0 mm block, a comment block reading move to point C, and a move arm to position x 125 y 175 z 0 mm block. The four new blocks are highlighted with a red box.

The project as is will only draw two sides of the triangle. The 6-Axis Arm needs to go back to point A to complete the triangle.

Add a Comment block to the stack and label it 'Return to point A' as well as adding a Move to position block.

Set the parameters of the Move to position blocks to the coordinates of point A.

The stack of blocks from before with a comment block reading return to point A and a move arm to position x 125 y 125 z 0 mm added to the bottom that is highlighted with red box.

Be sure to rename and save your project to your device.

The VEXcode Toolbar showing the project name that reads Unit 5 Lesson 3. The project name is highlighted with a red box.

Be sure the 6-Axis Arm is connected to VEXcode. Run your project.

The 6-Axis Arm will start at point A, then move to point B to draw the first side of the triangle. It will then continue to point C, drawing the second side of the triangle. The 6-Axis Arm will then move back to point A to complete the triangle by drawing the third side.

Stop the project once the 6-Axis Arm has finished moving.

An angled view of the 6-Axis Robotic Arm with the Pen Holder tool, having finished drawing a right triangle on the whiteboard.

Activity

Now that you have learned how to find missing coordinates given an initial coordinate and two side lengths, you will practice this skill. In this activity, you will build on your project from this Lesson to draw a square.

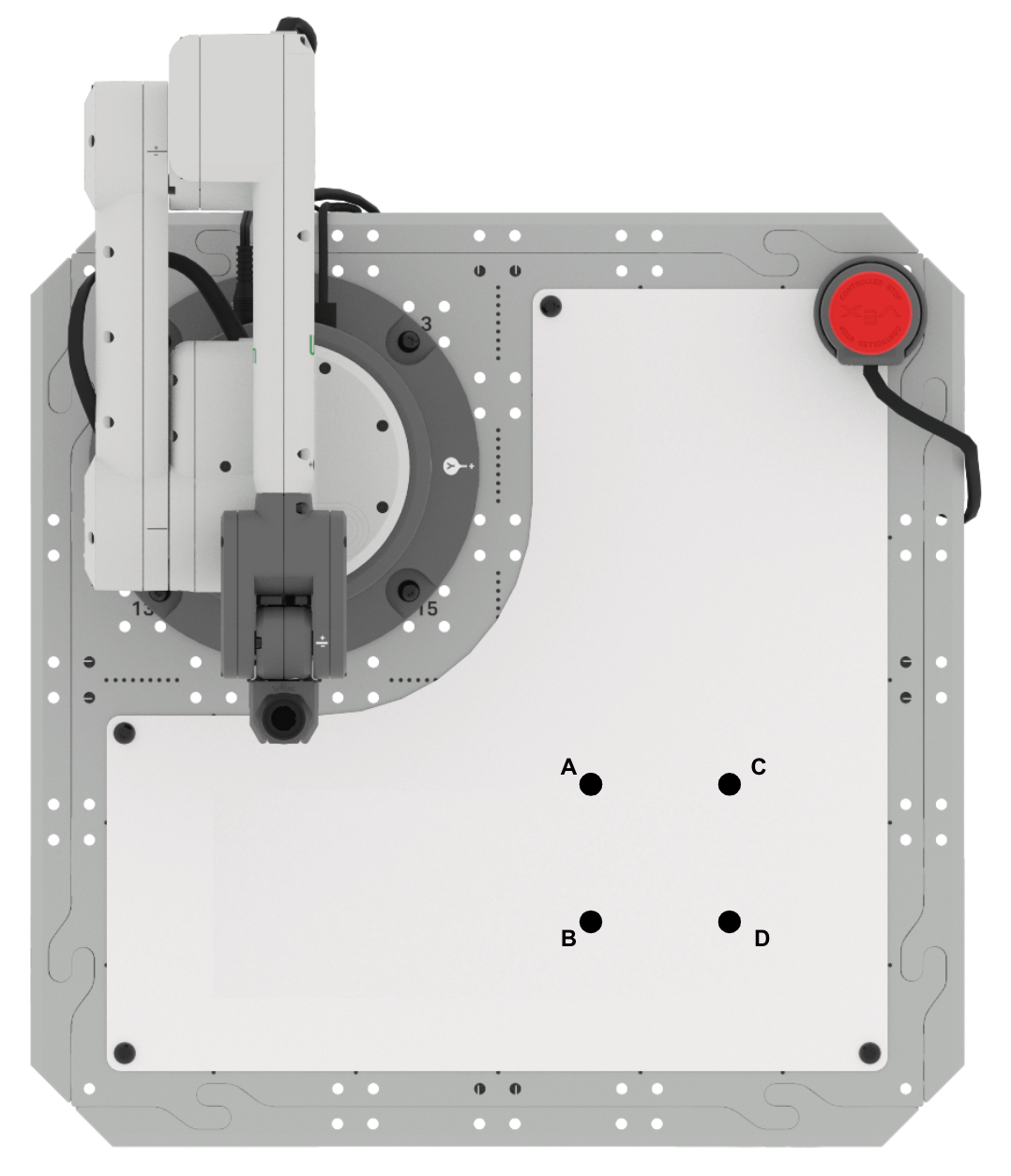
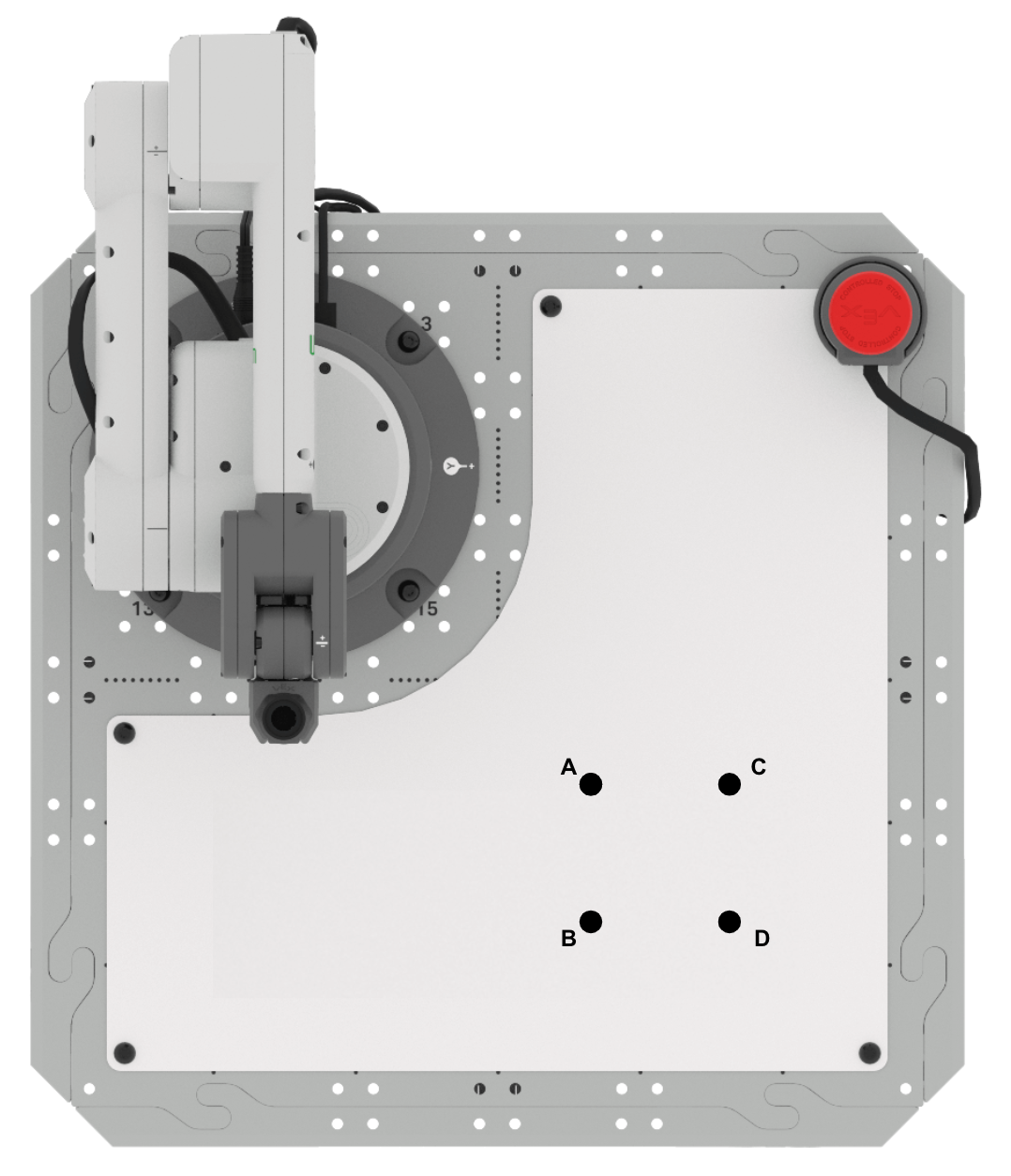
A top down view of the 6-Axis Robotic Arm over a whiteboard with the Pen Holder tool. 4 coordinates labeled A through D form a square shape on the whiteboard.

Setup: Draw points A, B, C, and D in your engineering notebook as shown above. You can use the information about triangle ABC from this Lesson to help you find the missing point D.
- Point A is located at (125, 125, 0)
- Point B is located at (175, 125, 0)
- Point C is located at (125, 175, 0)
- Side lengths AB and AC are 50mm
Activity: Find the coordinates of point D. Build onto your project from this Lesson to draw a square.
- Once you have edited your project, run it to test. Does the 6-Axis Arm successfully draw all four sides of the square? If not, modify your project and test it again.
- Record the process you used to find point D in your engineering notebook, and include details about how you used point D in your VEXcode project.

Check Your Understanding

Before moving to the next Lesson, ensure that you understand the concepts in this Lesson by answering the questions in the document below in your engineering notebook.

Check Your Understanding questions > (Google Doc / .docx / .pdf)

Select Next > to learn how to draw more triangles in different orientations.