Les 4: Een diamant tekenen
In de vorige lessen hebt u geleerd hoe u een driehoek tekent door de ontbrekende coördinaten te vinden. In deze les leert u wat u moet doen als de 6-assige arm langs de x- of y-as in negatieve richting beweegt en hoe u ontbrekende coördinaten berekent.
Aan het eind van deze les ga je een ruit tekenen door de coördinaten die je hebt bepaald met elkaar te verbinden.
Ontbrekende coördinaten vinden
In les 3 hebt u de ontbrekende coördinaten van een driehoek bepaald. Hiervoor hebt u één punt van de driehoek en de lengte van twee zijden gekend. Nu ga je op dat project voortbouwen om een tweede driehoek te tekenen.
Punt D vinden
Maak een schets van de bekende informatie in je technische notitieboekje.
Driehoek ABC bevindt zich in de punten:
- Een (125, 125, 0)
- B (175, 125, 0)
- C (125, 175, 0)
Dit is de driehoek die je in Les 3 tekende.
De tweede driehoek, ADE, heeft zijden van 50 mm, voor zijden AD en AE. De zijden van driehoek ADE worden in deze afbeelding weergegeven met blauwe lijnen en tekst.
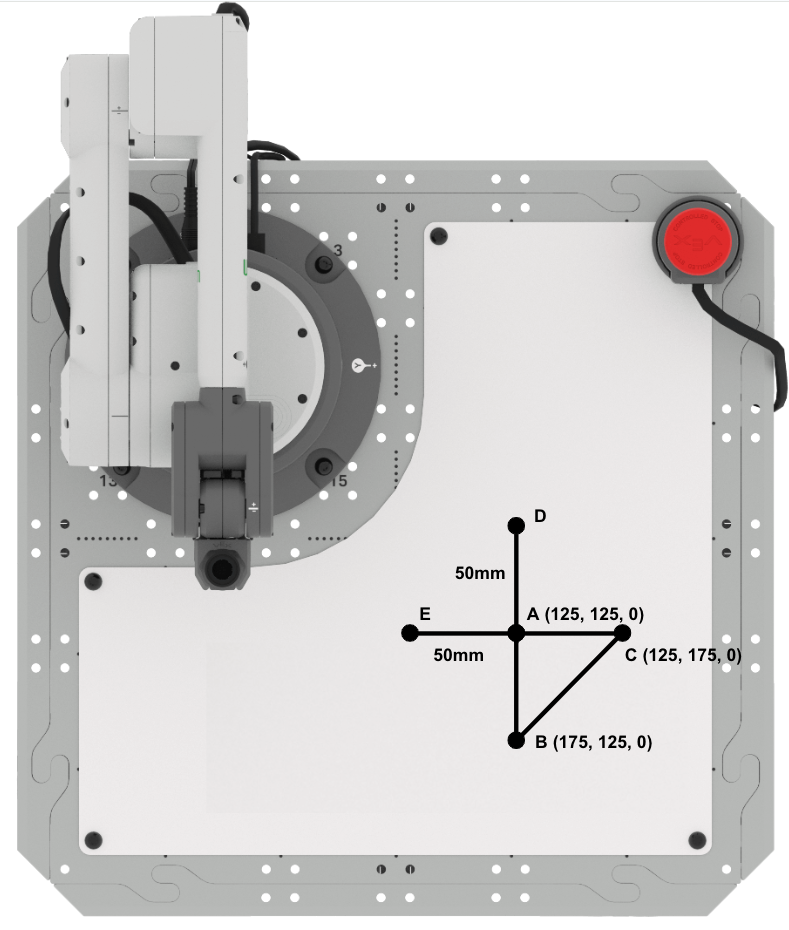
Zijde AD van rechthoekige driehoek ADE is evenwijdig aan de x-as.
Houd er rekening mee dat als u van punt A naar punt D langs de x-as beweegt, de x-coördinaten een waarde vanmin krijgen. Dit wordt weerspiegeld in de vergelijking die wordt gebruikt om de x-coördinaat van punt D te berekenen.
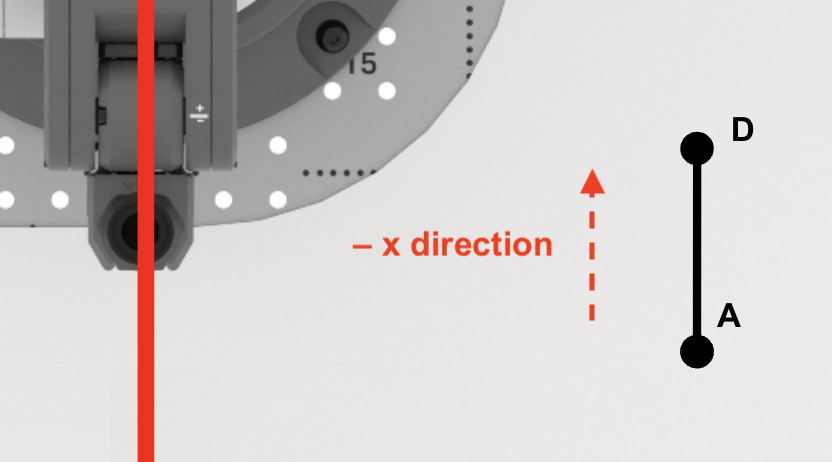
Bepaal de x-coördinaat van punt D.
Omdat de 6-assige arm in negatieve richting langs de x-as beweegt, moet u aftrekken. Trek de lengte van AD af van de x-coördinaat van punt A om de x-coördinaat van punt D te vinden.
De x-coördinaat van punt D is 75 mm. Noteer dit in uw technisch notitieboekje.

Vervolgens bepalen we de y-coördinaat van punt D.
Omdat de punten A, B en D langs de lijn y=125 mm liggen, is de y-coördinaat van punt D hetzelfde als die van de punten A en B (125 mm). Noteer dit in uw technisch notitieboekje.
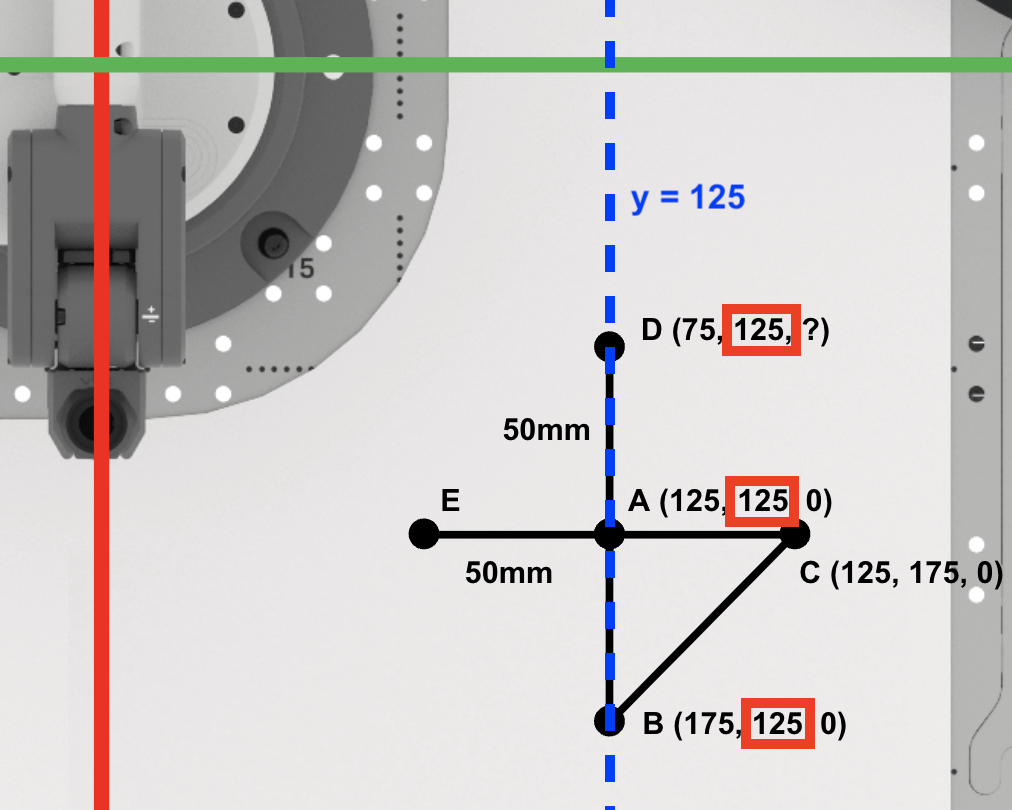
Omdat de Pen niet omhoog gaat tussen de punten A en D, blijft de z-coördinaat van punt D nul.
Punt D is (75, 125, 0). Noteer dit in uw technisch notitieboekje.
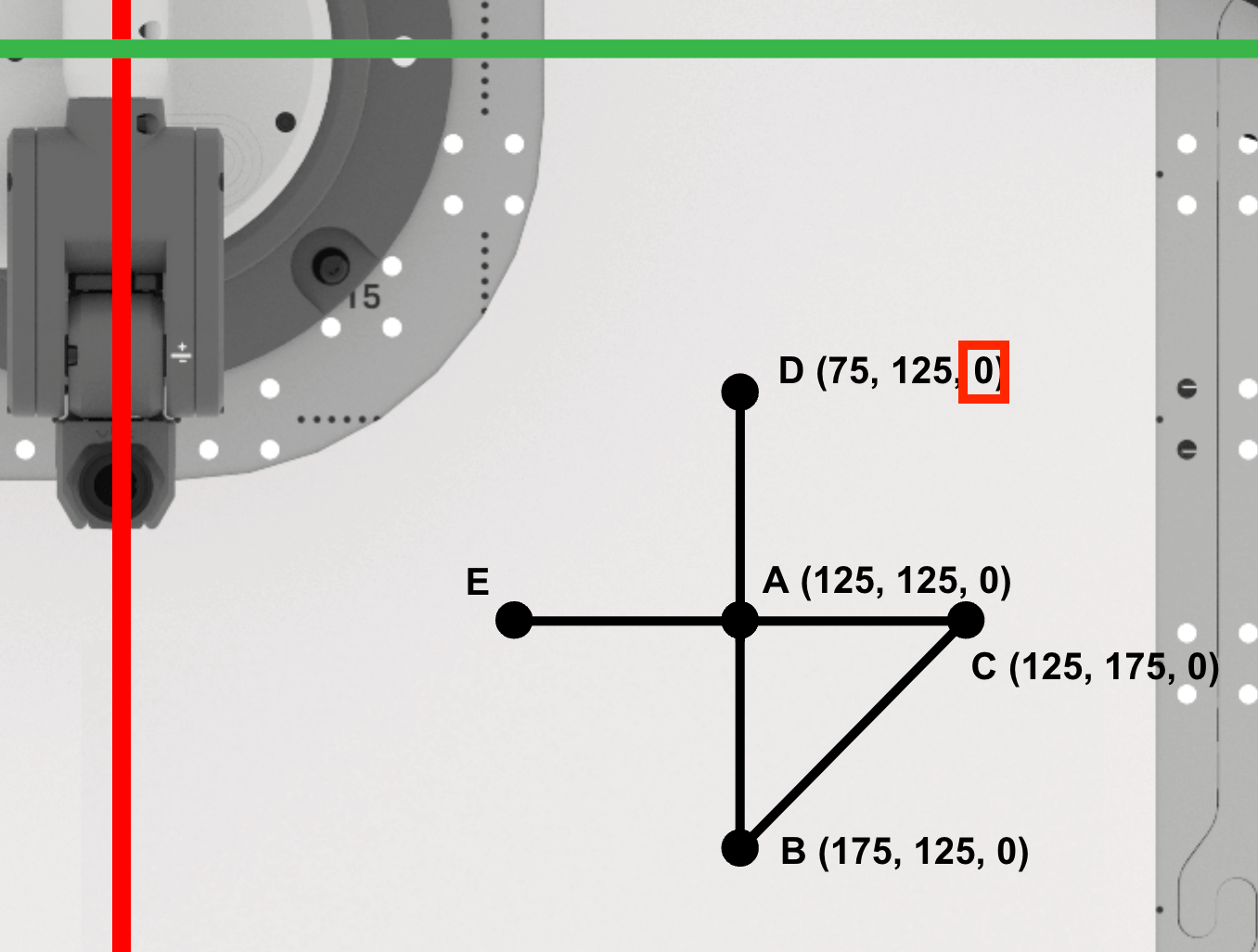
Punt E vinden
Bepaal de x-coördinaat van punt E.
Omdat de punten A, C en E langs de lijn x=125 mm liggen, is de x-waarde van punt E gelijk aan die van de punten A en C (125 mm).
Noteer dit in uw technisch notitieboekje.
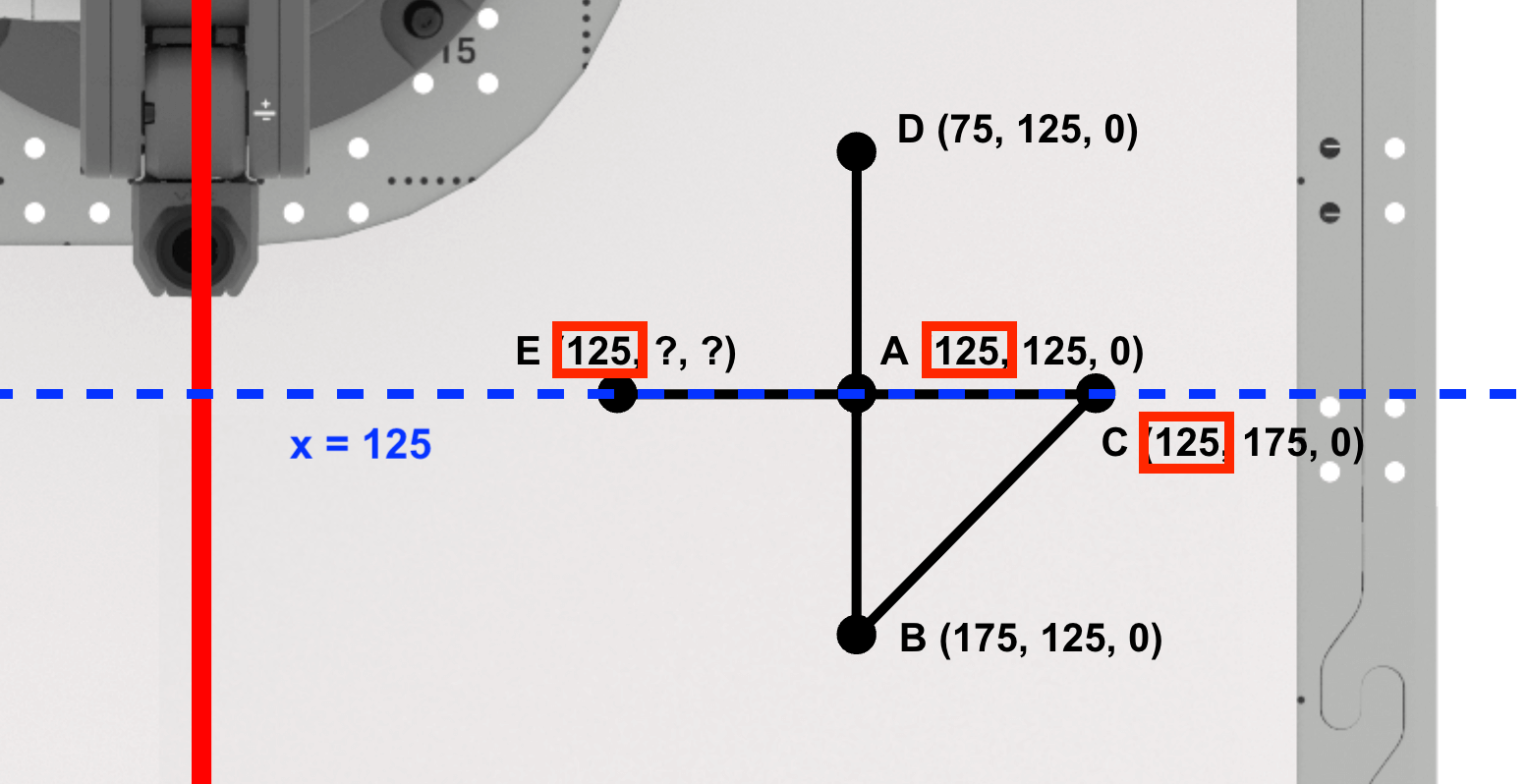
Zijde AE van de rechthoekige driehoek ADE is evenwijdig aan de y-as.
Houd er rekening mee dat als u van punt A naar punt E langs de y-as beweegt, de y-coördinaten een waarde vankleiner dan krijgen. Dit wordt weerspiegeld in de vergelijking die wordt gebruikt om de y-coördinaat van punt E te berekenen.

Bepaal vervolgens de y-coördinaat van punt E.
Omdat de 6-assige arm in negatieve richting langs de y-as beweegt, moet u aftrekken. Trek de lengte van AE af van de y-coördinaat van punt A om de y-coördinaat van punt E te vinden.
De y-coördinaat van punt E is 75 mm. Noteer dit in uw technisch notitieboekje.
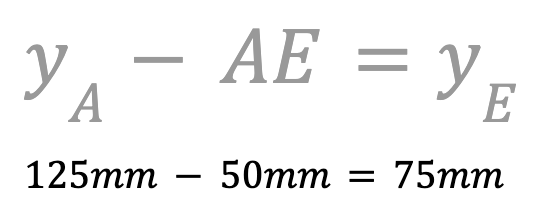
Omdat de Pen niet omhoog gaat tussen de punten D en E, blijft de z-coördinaat van punt E nul.
Punt E is (125, 75, 0). Noteer dit in uw technisch notitieboekje.
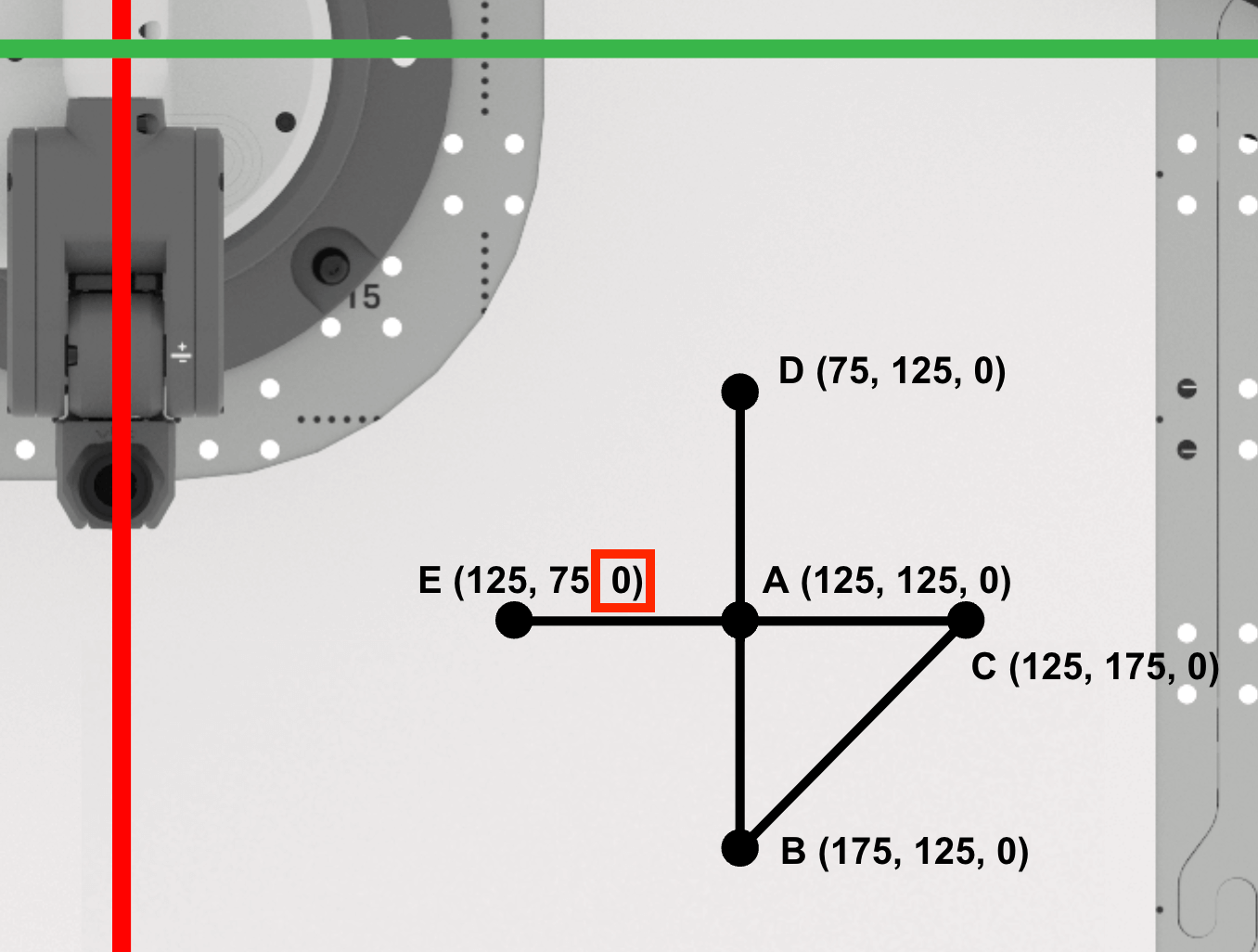
Het coderen van de 6-assige arm om een driehoek te tekenen ADE
Nu u de coördinaten voor de punten D en E hebt bepaald, is het tijd om een VEXcode EXP-project voor de 6-assige arm te maken om de punten A, D en E te verbinden om zo een andere driehoek te tekenen.
Open het project Unit 5 Les 3 om driehoek ABC op het whiteboard te tekenen, of maak het project na zoals hier getoond.

Wijzig het hier getoonde blok Commentaar naar "Verplaats naar punt A om de eerste driehoek te starten."
Omdat u twee driehoeken tekent, kunt u de opmerking wijzigen om context te geven over welke blokken in het project worden gebruikt om de eerste driehoek te tekenen en welke niet.
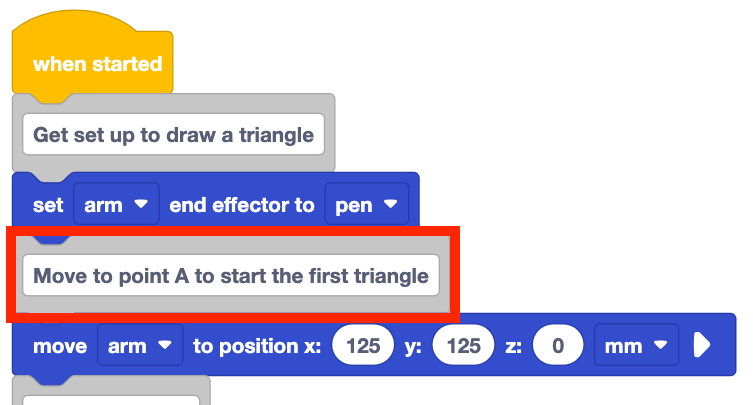
Voeg een blok Comment toe aan de onderkant van de stapel en typ "Verplaats naar punt D om de tweede driehoek te beginnen."
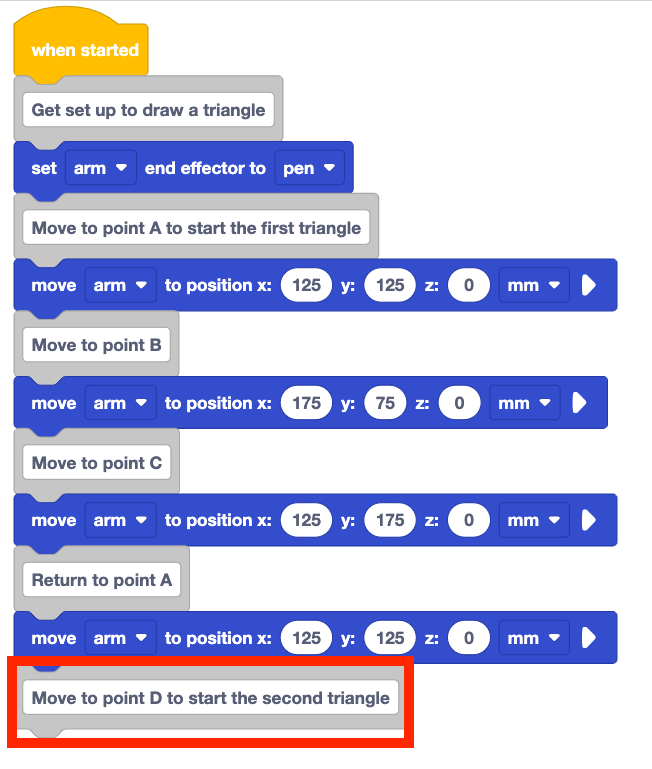
Voeg een Verplaats naar positie blok toe aan de stapel onder het Commentaar blok.
Stel de parameters van op de coördinaten van punt D, zoals vastgelegd in uw technisch notitieboekje.

Voeg opmerkingen toeblokken en Verplaats naar positie blokken voor punt E en keer terug naar punt A om de tweede driehoek te voltooien.
Stel de parameters van de blokken Verplaats naar positie in op de coördinaten van de punten E en A, die u in uw technisch notitieboekje hebt genoteerd.
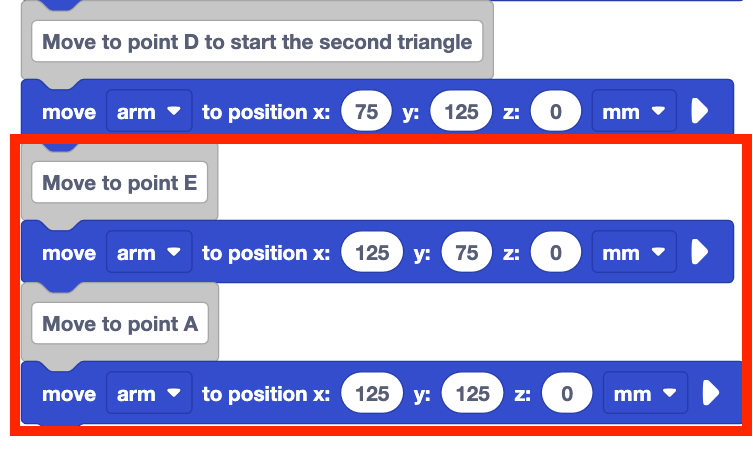
Zorg ervoor dat u het project een nieuwe naam geeft en opslaat op uw apparaat.

Wanneer het project voltooid is, zou het er als volgt uit moeten zien.
Wanneer u klaar bent met het bouwen van uw project, zorg er dan voor dat de 6-assige arm is aangesloten op VEXcode EXP en voer het project uit.

Stop het project wanneer de 6-assige arm klaar is met het tekenen van de twee driehoeken.
De 6-assige arm tekent driehoek ABC zoals in les 3. Vervolgens beweegt het naar punt D om de eerste zijde van driehoek ADE te tekenen. Vervolgens beweegt de 6-assige arm van punt D naar punt E om de tweede zijde van driehoek ADE te voltooien. Vervolgens maakt hij de driehoek af door het pakket naar punt A te verplaatsen.
Opmerking:Deze afbeelding toont de 6-assige arm die handmatig is verplaatst nadat het project was gestopt, zodat beide driehoeken duidelijk te zien zijn.

Activiteit
In deze les hebt u geleerd hoe u driehoeken tekent met zijden die in negatieve richting langs de assen moeten worden verplaatst. Nu ga je wat je hebt geleerd in de praktijk brengen om een ruit te tekenen, die bestaat uit vier driehoeken.

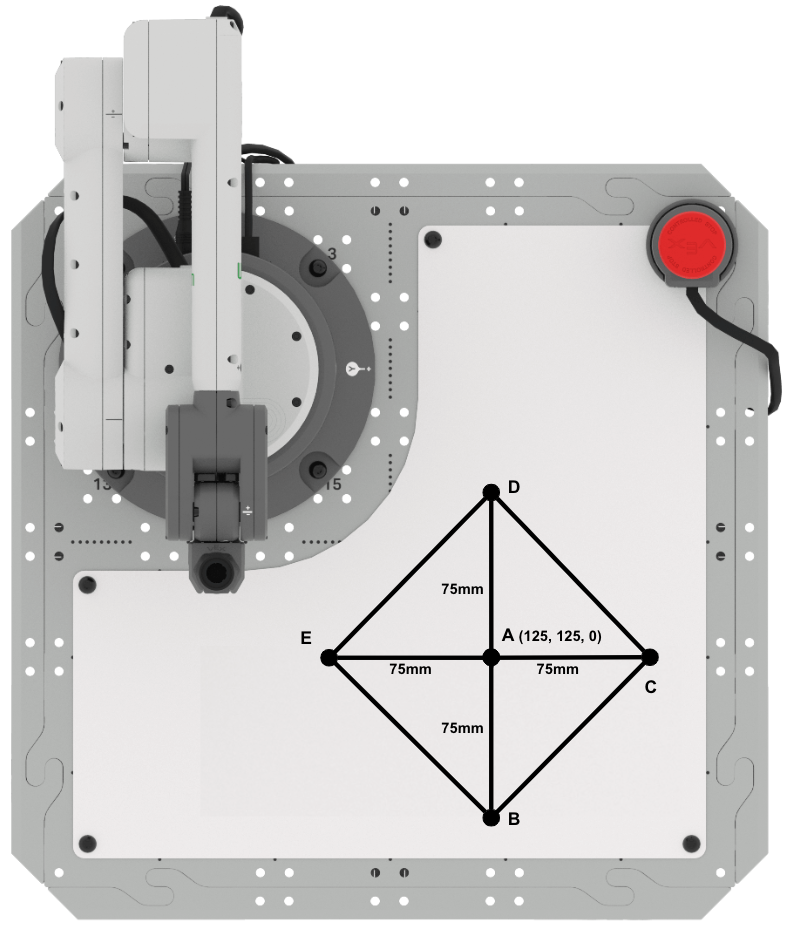
- Opstelling:Teken de punten A, B, C, D en E in je technisch notitieboekje zoals hierboven weergegeven.
- Punt A bevindt zich op (125, 125, 0)
- Zijlengtes AB, AC, AD en AE zijn 75 mm
- Activiteit:
- Gebruik de formules uit les 3 en 4 om de coördinaten van de bovenstaande punten B, C, D en E te bepalen. Noteer de coördinaten in uw technisch notitieboekje.
- Maak een VEXcode EXP-project om de punten te verbinden en de hierboven getoonde vorm te tekenen.
- U kunt verder bouwen op het project Les 4, of het project Signal Tower Template.
- Zorg ervoor dat u het eind-effectorblok instelt op penom te beginnen.
- Gebruik opmerkingen om het gedrag van de 6-assige arm in uw project te communiceren.
- Wanneer u klaar bent met het bouwen van uw project, voert u het project uit om het te testen.
- Heeft jouw project de hierboven getoonde diamant getekend? Als dat niet lukt, blijf dan uw project aanpassen en testen totdat het wel lukt.
- Nadat u het project hebt voltooid, geeft u het een nieuwe naam en slaat u het op op uw apparaat.
Controleer uw begrip
Voordat u doorgaat naar de volgende les, moet u ervoor zorgen dat u de concepten in deze les begrijpt door de vragen in het onderstaande document in uw technische notitieboekje te beantwoorden.
Controleer uw begrip vragen > (Google Doc / .docx / .pdf)
SelecteerVolgende >om de activiteit Alles bij elkaar voegen te voltooien.