En esta lección, aprenderá sobre el sistema de coordenadas cartesianas utilizado con el brazo robótico de 6 ejes.
Al final de esta lección, utilizará su comprensión del sistema de coordenadas cartesianas y su relación con el brazo de 6 ejes para estimar las coordenadas de tres ubicaciones de mosaicos CTE.
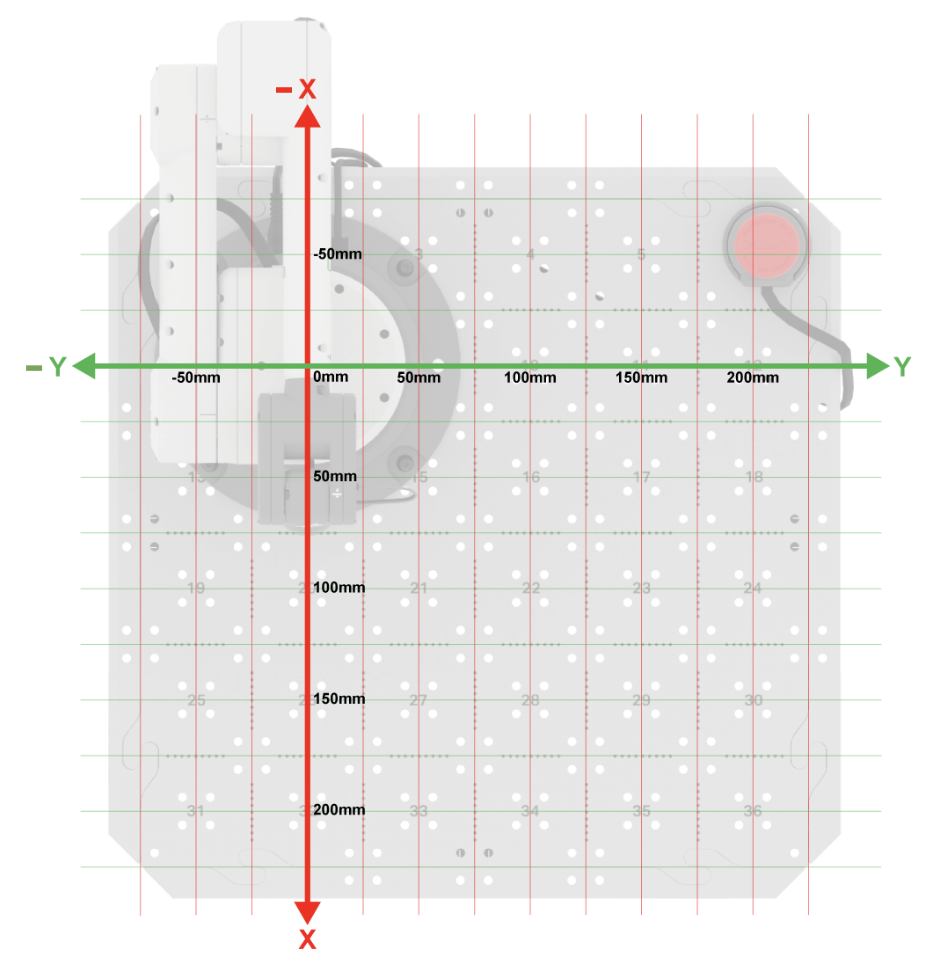
Sistema de coordenadas cartesianas
Para mover el brazo de 6 ejes en el espacio, necesitamos tener un marco de referencia común para que el brazo de 6 ejes pueda moverse a la ubicación deseada. El brazo de 6 ejes utiliza el sistema de coordenadas cartesianas para determinar dónde se encuentra el extremo del brazo de 6 ejes.
Ejes X, Y y Z
Un sistema de coordenadas es una cuadrícula matemática de valores. Existen diferentes tipos de sistemas de coordenadas, pero el sistema de coordenadas cartesianas se utiliza con el brazo de 6 ejes. Esto también se conoce como sistema 3D (dimensional), ya que sus tres dimensiones son los ejes x, y y z.
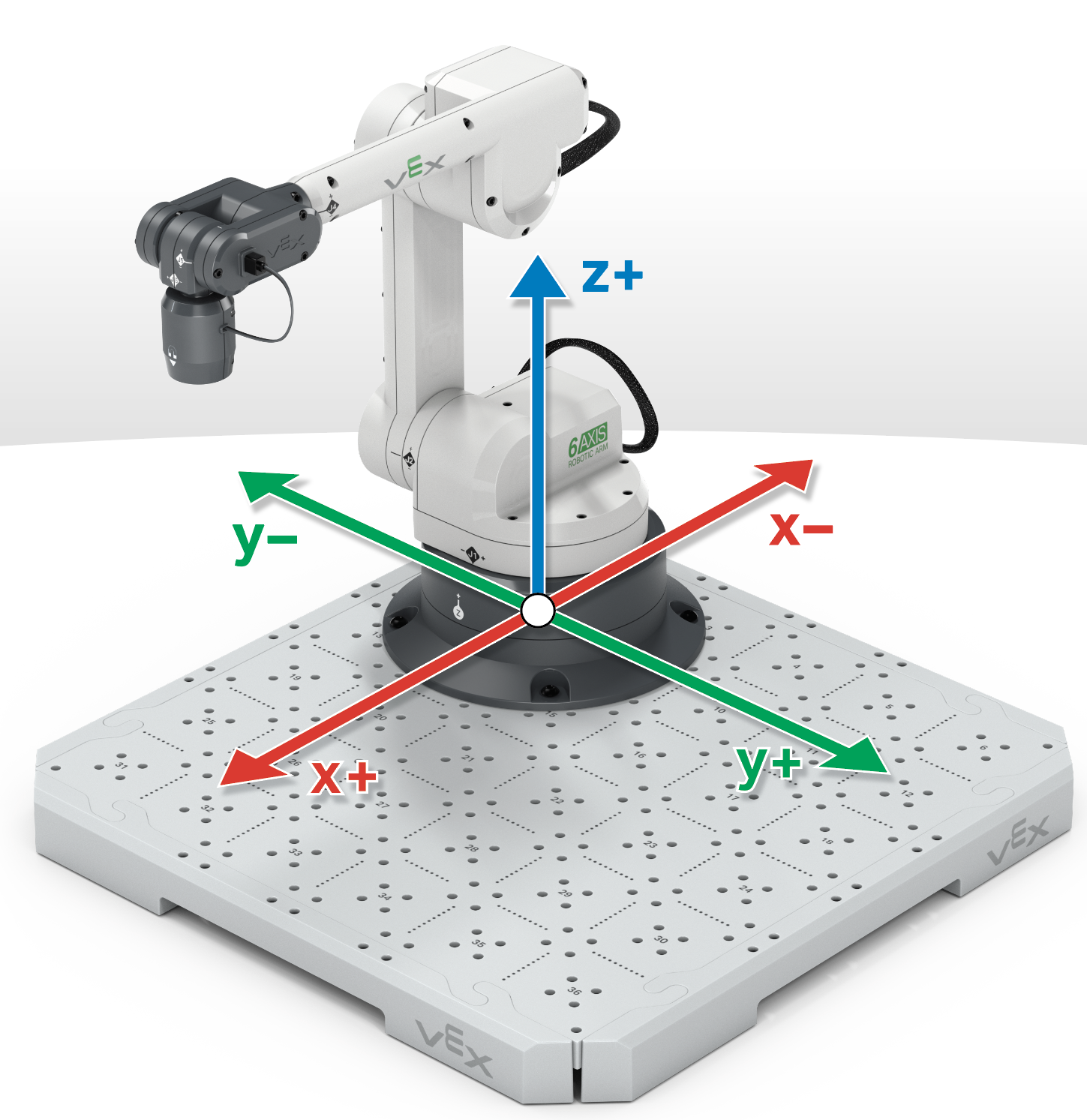
El eje x se puede demostrar moviendo el brazo de 6 ejes hacia la base (retraído) y alejándolo de la base (extendido).
El eje y se puede demostrar moviendo el brazo de 6 ejes a la izquierda y derecha de la base.
El eje z se puede demostrar moviendo el brazo de 6 ejes hacia abajo hacia la baldosa y luego hacia arriba lejos de la baldosa.
Estimación de coordenadas
La coordenada (x, y, z) está determinada por la distancia desde la coordenada (0, 0, 0), también llamada origen, hasta el final del brazo de 6 ejes, llamado punto central de la herramienta (TCP).
El origen o (0, 0, 0) es la ubicación desde la que comienzan todos los valores. El (0, 0, 0) en el brazo de 6 ejes se encuentra en el centro de la base.

El extremo del brazo de 6 ejes se conoce como el punto central de la herramienta (TCP).
Para el brazo de 6 ejes en esta imagen, el TCP está al final de la herramienta de recogida de imanes.
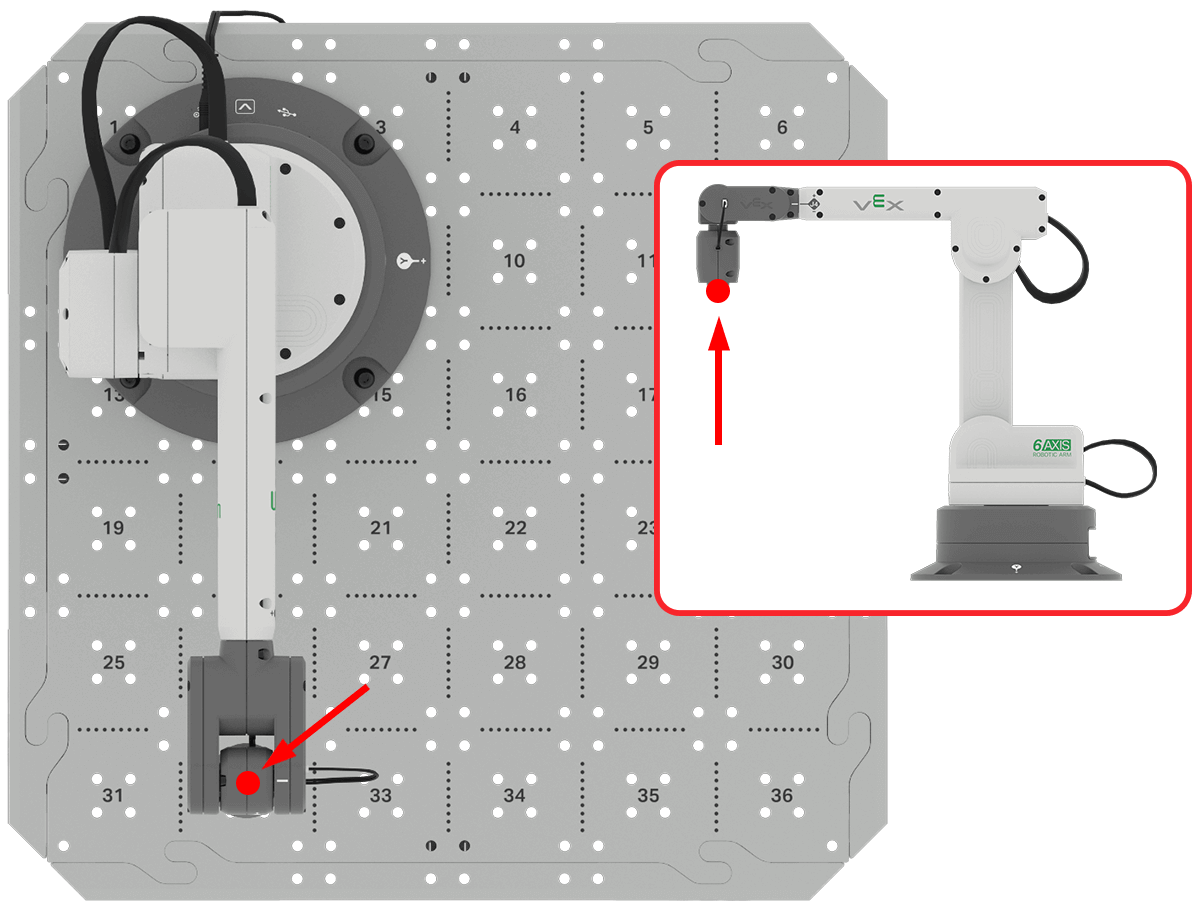
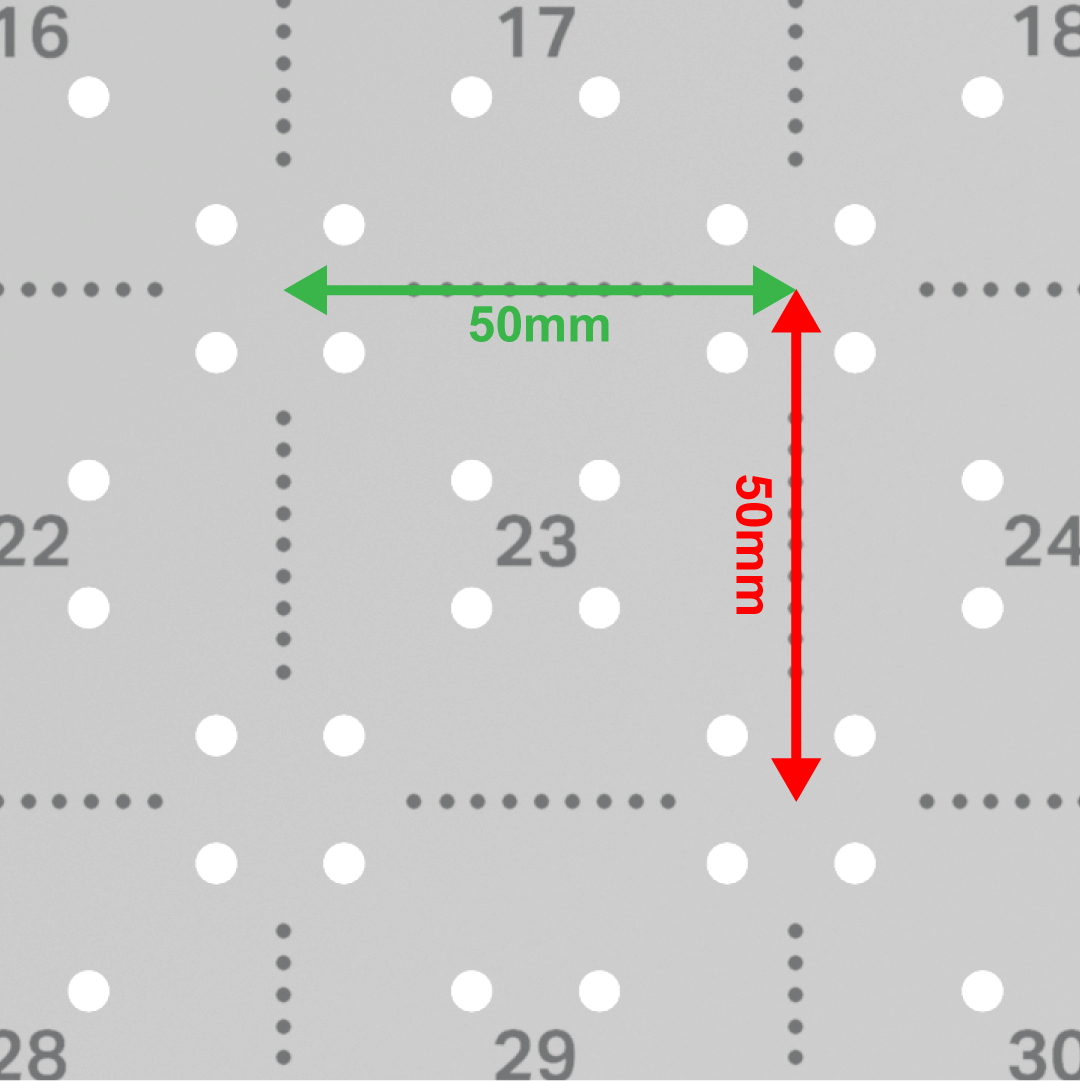
Puede usar la imagen aquí para ayudar a determinar las coordenadas x, y del brazo de 6 ejes. El eje z se mostrará en la siguiente cuadrícula.
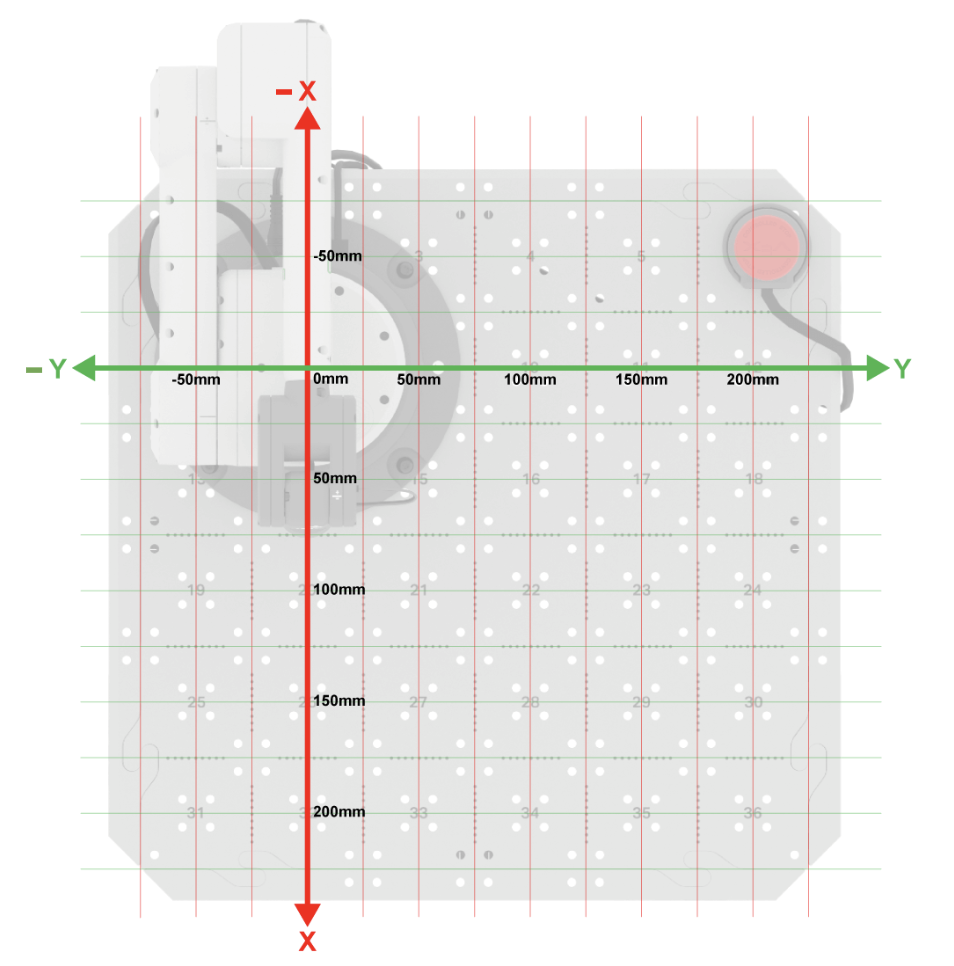
La medida de cada uno de los cuadrados individuales en la baldosa es de 50 mm por 50 mm.
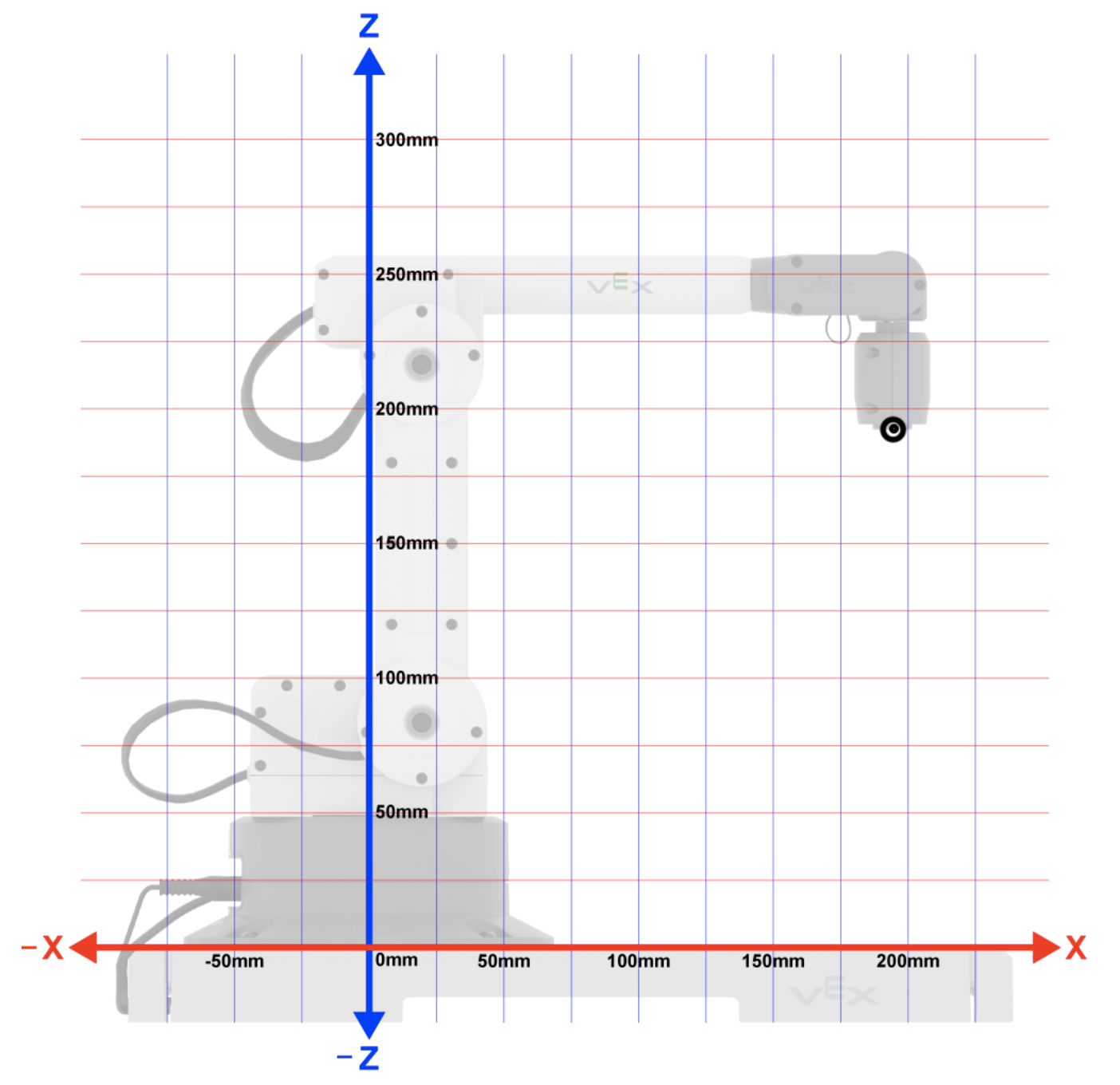
La recopilación del valor del eje z se puede hacer determinando la distancia desde el mosaico hasta el TCP.
En este ejemplo, el valor z del TCP se puede estimar en poco menos de 200 mm utilizando la cuadrícula de coordenadas.
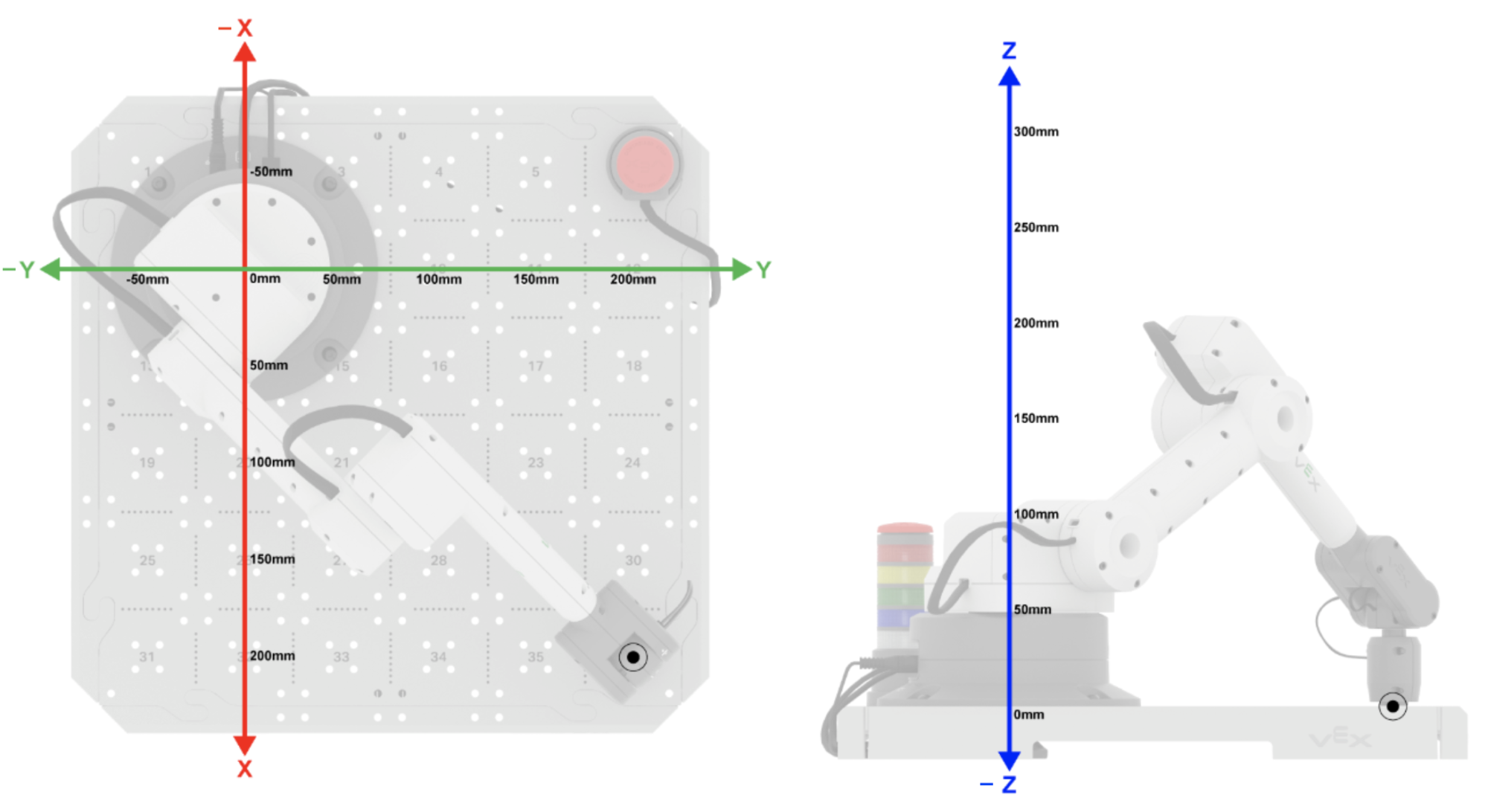
La coordenada (x, y, z) está determinada por la distancia (en milímetros) desde el origen hasta el TCP a lo largo de los tres ejes.
En este ejemplo, la coordenada (x, y, z) sería (200, 200, 0) porque el TCP está a 200 mm del origen en el eje x, 200 mm del origen en el eje y y 0 mm del origen en el eje z.
Actividad
Anteriormente, en esta lección, discutimos el sistema de coordenadas cartesianas y cómo determinar las coordenadas en función de la distancia desde el origen hasta el TCP. En esta actividad, determinarás las coordenadas de tres ubicaciones de mosaicos.
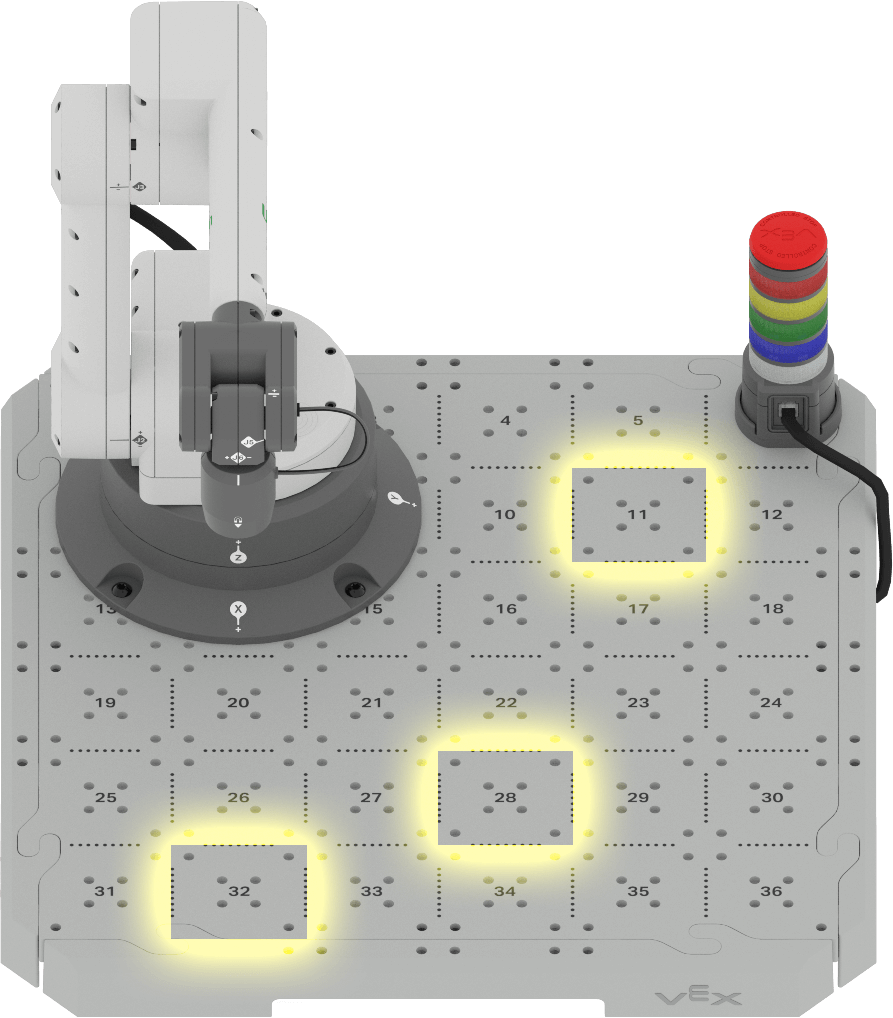
- Estimar las coordenadas (x, y, z) de las siguientes ubicaciones de mosaico. Suponga que el brazo de 6 ejes está tocando cada ubicación de la baldosa y la coordenada z es 0 mm.
- Ubicación del mosaico 11
- Ubicación del mosaico 32
- Ubicación del mosaico 28
- Registre estas coordenadas en su cuaderno de ingeniería. Explica cómo determinaste cada coordenada.
Compruebe su comprensión
Antes de comenzar la siguiente Lección, asegúrese de comprender los conceptos tratados en esta Lección respondiendo las preguntas del siguiente documento en su cuaderno de ingeniería.
Verifique sus preguntas de comprensión > (Google Doc / .docx / .pdf)
Seleccione Siguiente > para aprender a recopilar coordenadas utilizando los movimientos manuales.