Les 3: Ontbrekende coördinaten vinden

In de vorige lessen hebt u geleerd hoe u een driehoek op het whiteboard tekent met de penhoudertool. Alle punten van de driehoek zijn aangegeven. Als echter niet alle punten van de driehoek gegeven zijn, moeten deze wiskundig bepaald worden, zodat de 6-assige arm langs meerdere assen kan bewegen.

In deze les ga je op zoek naar de twee ontbrekende coördinaten van een driehoek, zodat je de driehoek kunt tekenen. Aan het einde van deze les ga je toepassen wat je hebt geleerd om op de driehoek een vierkant te tekenen.

Een bovenaanzicht van de 6-assige robotarm boven een whiteboard met de penhoudertool. 4 coördinaten, gelabeld A tot en met D, vormen een vierkant op het whiteboard.

Ontbrekende coördinaten vinden

De 6-assige arm gaat een driehoek tekenen. Dit is de informatie die we over deze driehoek weten:

Punt A is (125, 125, 0).
De lengte van elke zijde is 50 mm.
Driehoek ABC is een rechthoekige driehoek (een driehoek met een hoek van 90º).
- De zijde tegenover deze hoek is de langste zijde en wordt de hypotenusa genoemd. De andere twee kanten worden de benen genoemd.

Met behulp van deze informatie kunnen we de twee eindpunten (punten B en C) vinden om de driehoek te tekenen.

Volg de onderstaande stappen om de punten B en C te vinden en de driehoek te tekenen.

Punt B vinden

Maak een schets van de bekende informatie over de driehoek in je technisch notitieboekje.

Punt A ligt ongeveer op (125, 125, 0).

De afstand van punt A naar punt B bedraagt ongeveer 50 mm. De afstand van punt A naar punt C bedraagt ongeveer 50 mm. Elke afstand komt overeen met de lengte van de zijden van de driehoek.

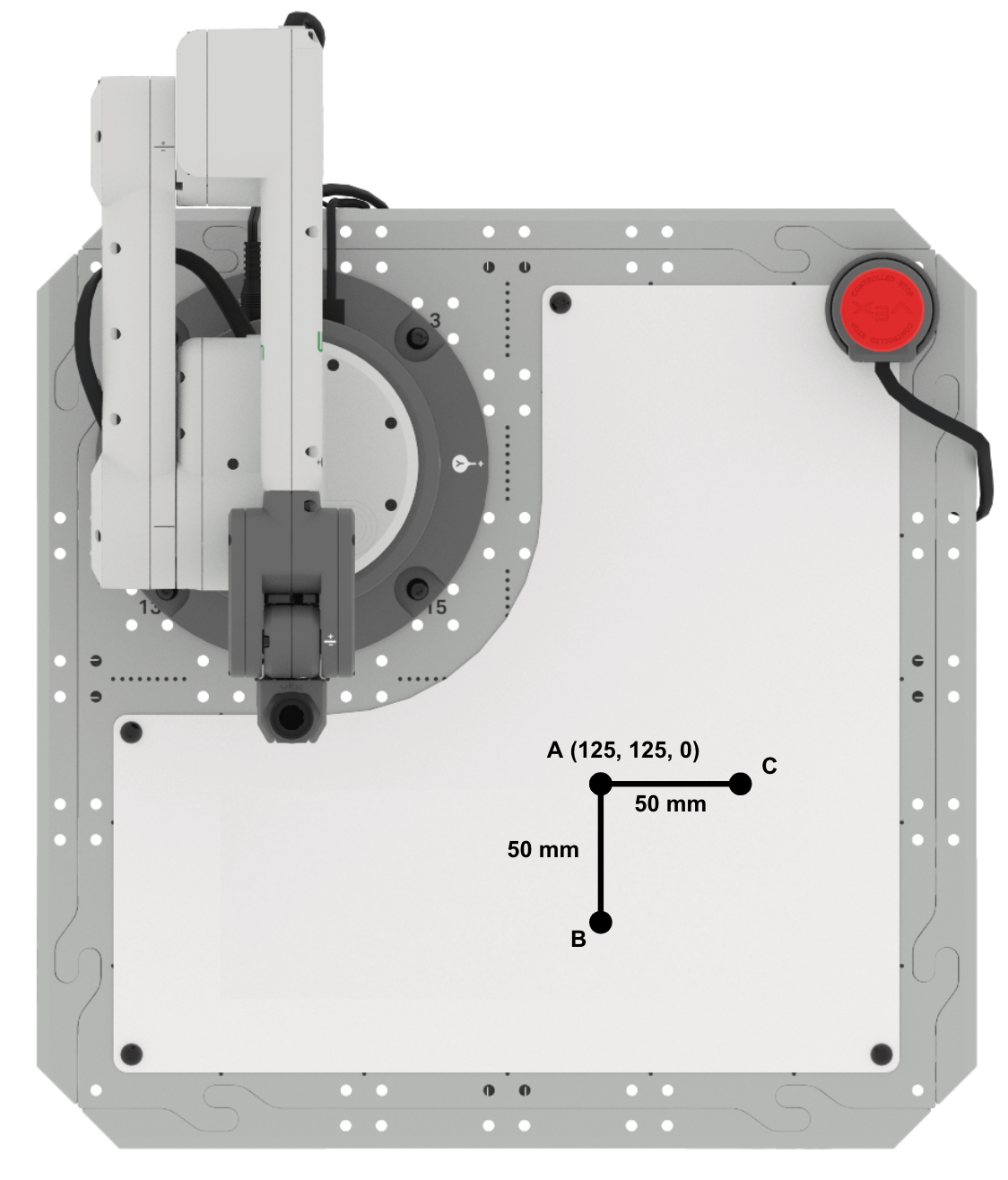
Een bovenaanzicht van de 6-assige robotarm boven een whiteboard met de penhoudertool. 3 coördinaten zijn gelabeld met A tot en met C. Coördinaat A is gelabeld met (125, 125, 0), waarbij 50 mm de afstanden tussen de coördinaten A en C en A en B aangeeft.

Bepaal de x-coördinaat van punt B. Dit kun je doen door de lengte van AB op te tellen bij de x-coördinaat van punt A om zo de x-coördinaat van punt B te vinden.

De x-waarde van punt B is 175 mm. Noteer dit in uw technisch notitieboekje.

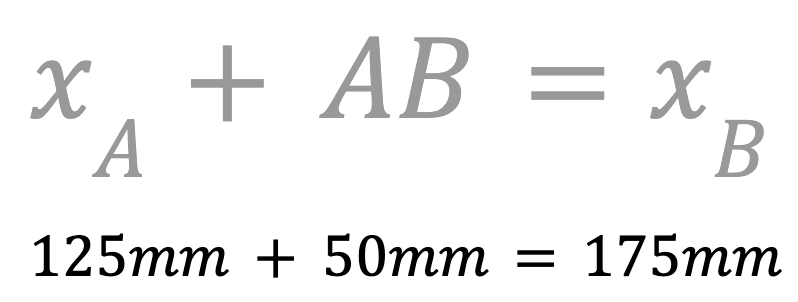
De formule voor het vinden van de x-coördinaat van B luidt: X van A + AB = x van B. De onderstaande formule luidt: 125 mm + 50 mm = 175 mm.

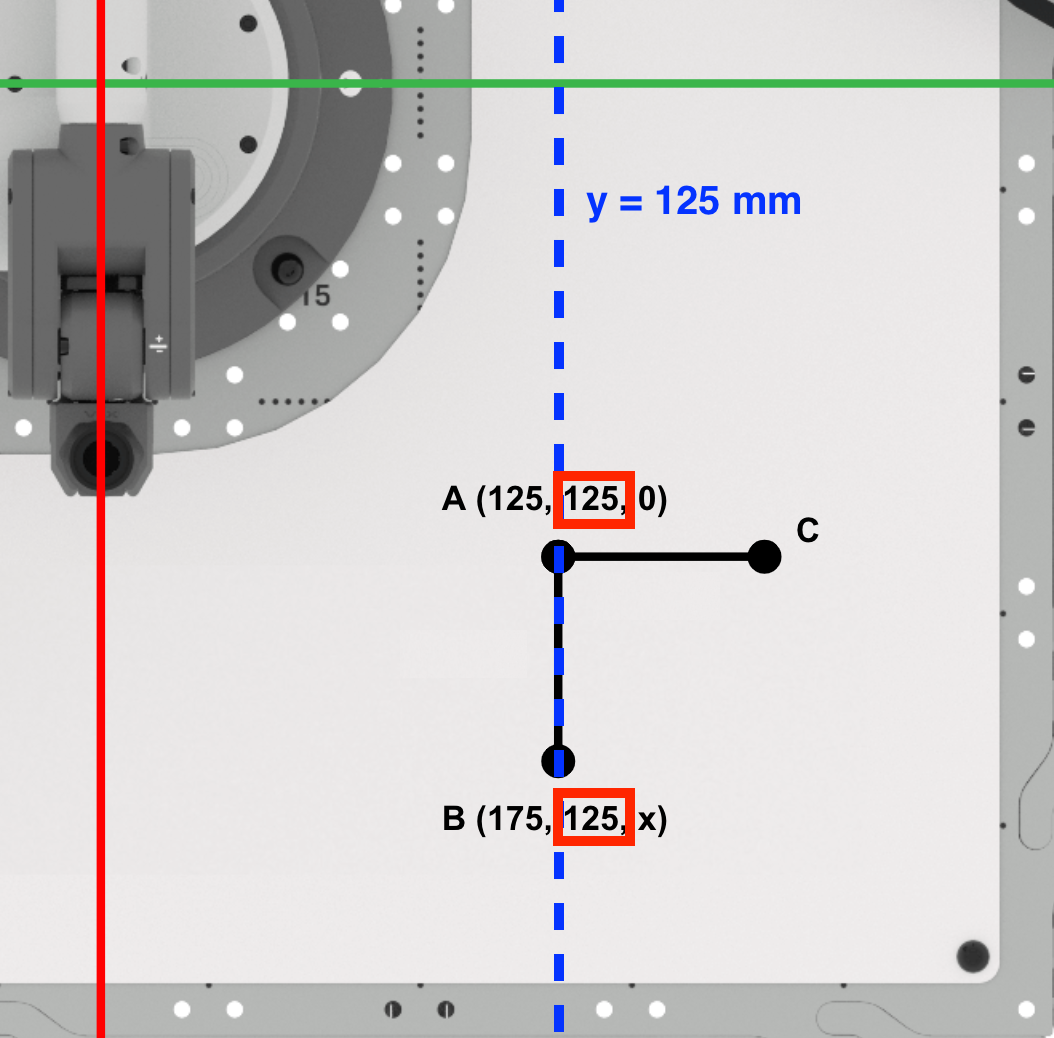
Vervolgens bepalen we de y-coördinaat van punt B.

Omdat de punten A en B langs de lijn y=125 mm liggen, is de y-coördinaat van punt B gelijk aan die van punt A (125 mm). Noteer dit in uw technisch notitieboekje.

Een bovenaanzicht van de 6-assige robotarm en de tegel, met een raster waarop de X- en Y-assen zijn gelabeld. De A-coördinaat van hiervoor is gelabeld als (125, 125, 0) met de B-coördinaat eronder gelabeld als (175, 125, x). Een blauwe lijn vanaf de rasterlijn van de Y loopt door beide coördinaten en is gemarkeerd met y = 125 mm. Beide y-coördinaten van A en B worden gemarkeerd met een rood kader.

Omdat de pen niet omhoog gaat tussen punt A en B, blijft de z-coördinaat van punt B nul.

Punt B is (175, 125, 0). Noteer dit in uw technisch notitieboekje.

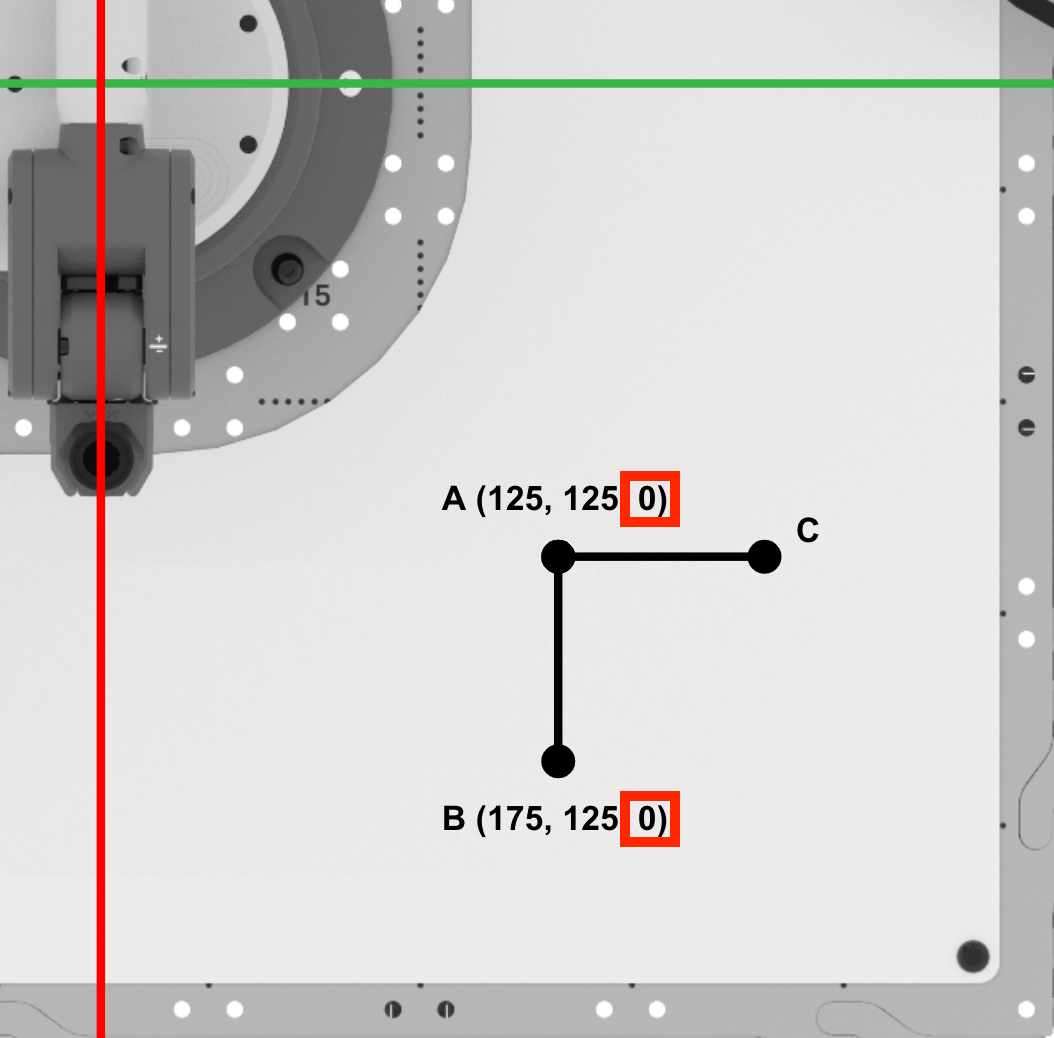
Punt C vinden

Bepaal de x-coördinaat van punt C.

Omdat de punten A en C langs de lijn x=125 mm liggen, is de x-waarde van punt C gelijk aan die van punt A (125 mm).

Noteer dit in uw technisch notitieboekje.

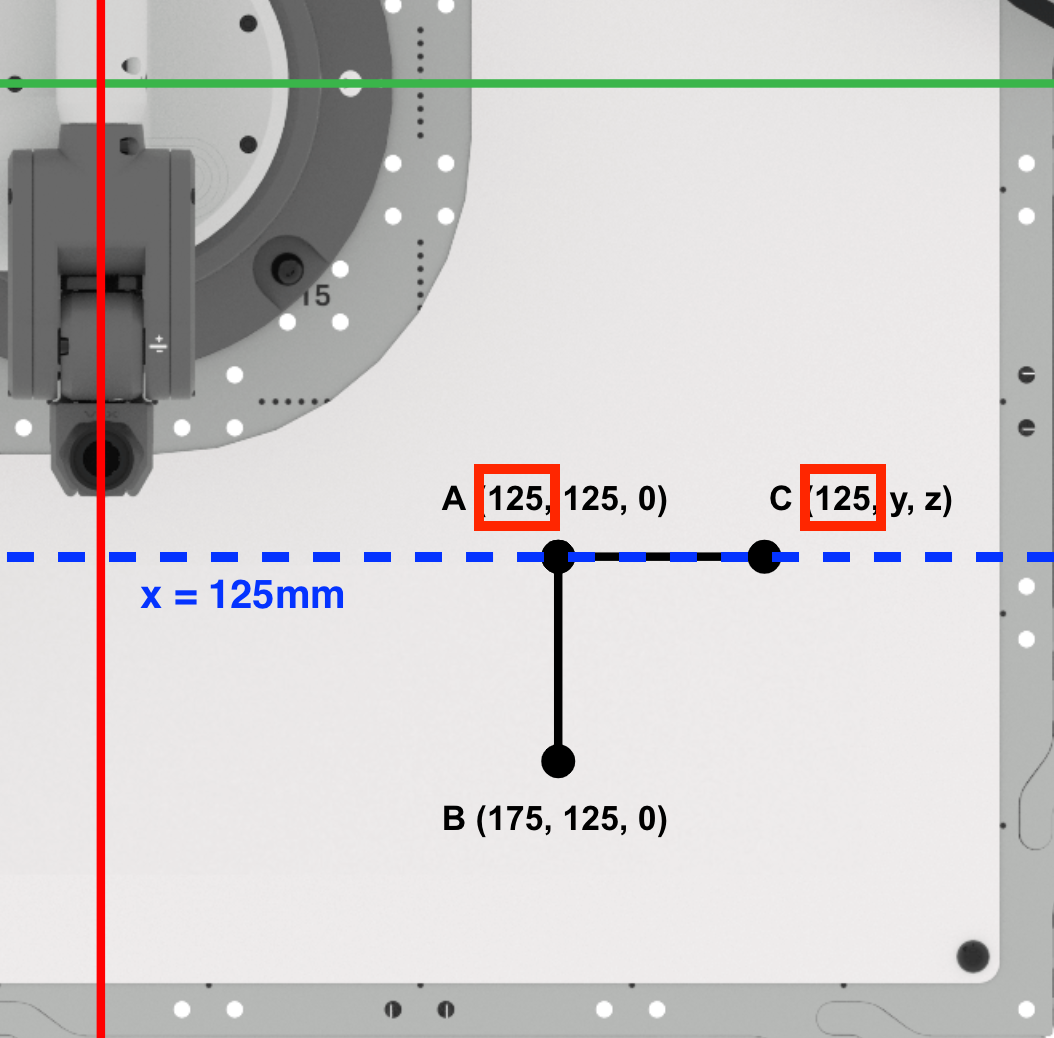
Bepaal vervolgens de y-coördinaat van punt C.

Omdat we een rechthoekige driehoek tekenen, weten we dat zijde AC evenwijdig is aan de y-as. Tel de lengte van AC op bij de y-coördinaat van punt A om de y-coördinaat van punt C te vinden.

De y-coördinaat van punt C is 175 mm. Noteer dit in uw technisch notitieboekje.

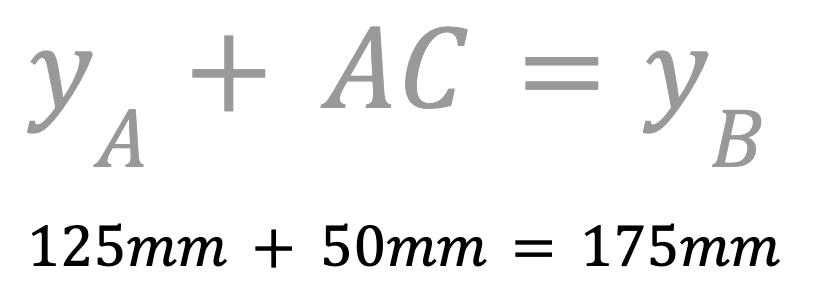
Een formule om de y-waarde van punt C te berekenen, waarbij y onderschrift A + AC = y onderschrift B staat. Daaronder staat 125 mm + 50 mm = 175 mm.

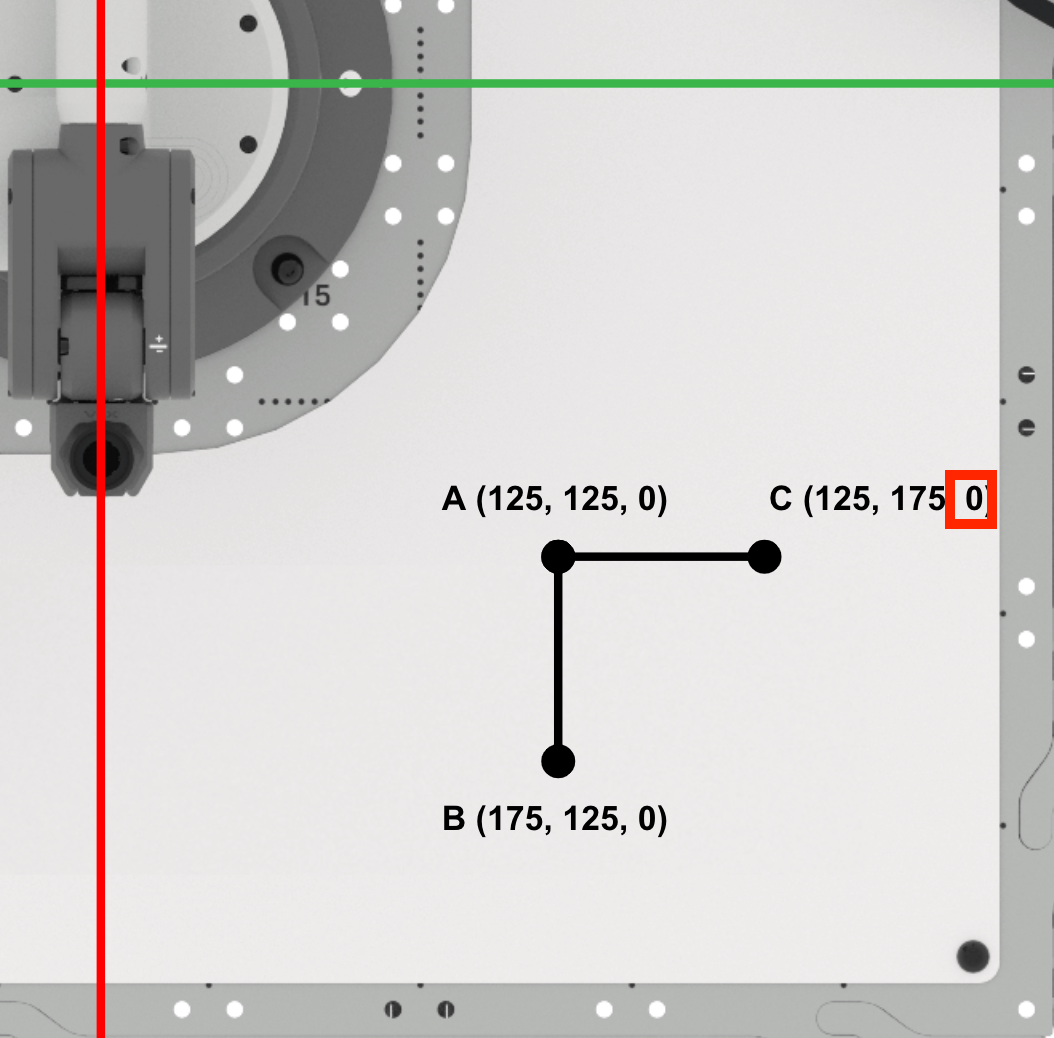
Omdat de Pen niet omhoog gaat tussen de punten A en C, blijft de z-coördinaat van punt C nul.

Punt C is (125, 175, 0). Noteer dit in uw technisch notitieboekje.

Het coderen van de 6-assige arm om punten A, B en C te verbinden

Nu u de coördinaten voor de punten B en C hebt bepaald, is het tijd om een VEXcode EXP-project voor de 6-assige arm te maken om de punten A, B en C te verbinden om een driehoek te tekenen.

Open eenNew Blocks Projectdoor de stappen in deze video te volgen. In de videoclip is Bestand geselecteerd in de werkbalk en vervolgens Nieuw blokproject. Er verschijnt een dialoogvenster met twee opties: EXP Brain aan de linkerkant en Arm aan de rechterkant. De optie Arm is geselecteerd en er wordt een nieuw project geopend in de werkruimte.

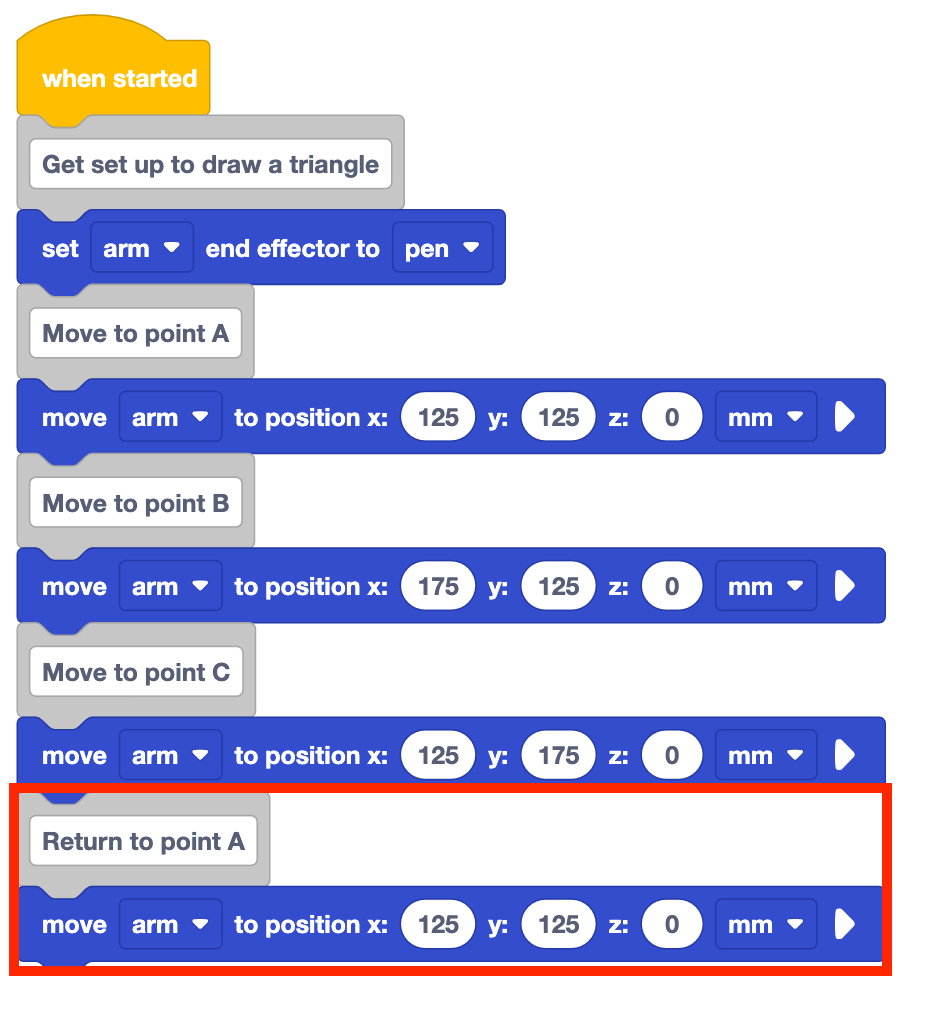
Voeg een blok Comment toe aan de stapel en typ 'Ga aan de slag om een driehoek te tekenen.'

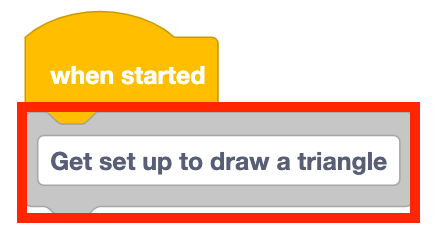
Een stapel blokken die begint met een when started-blok. Het volgende blok, het opmerkingenblok, luidt: Maak je klaar om een driehoek te tekenen. Het is gemarkeerd met een rood kader.

Voeg een Set end effector blok toe aan de stapel en stel deze in op 'pen'.

De stapel blokken van hiervoor, met een set arm-end-effector aan het penblok toegevoegd aan de onderkant. De tweede parameter van het blok is uitgevouwen en toont de magneet en de pen, waarbij de pen is geselecteerd. Het onderste blok wordt gemarkeerd met een rood kader.

Voeg een blok Comment toe aan de stapel en typ 'Verplaats naar punt A'.

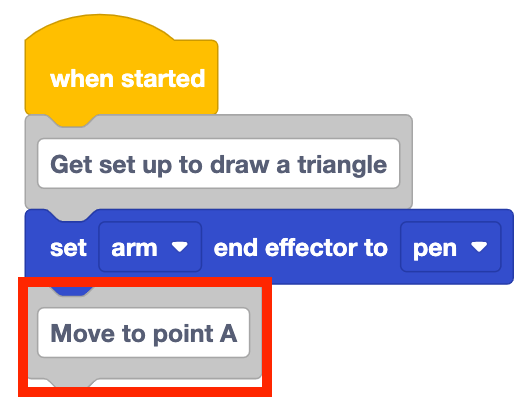
De stapel blokken van hiervoor met een commentaarblok met de tekst Verplaats naar punt A, dat is gemarkeerd met een rood kader.

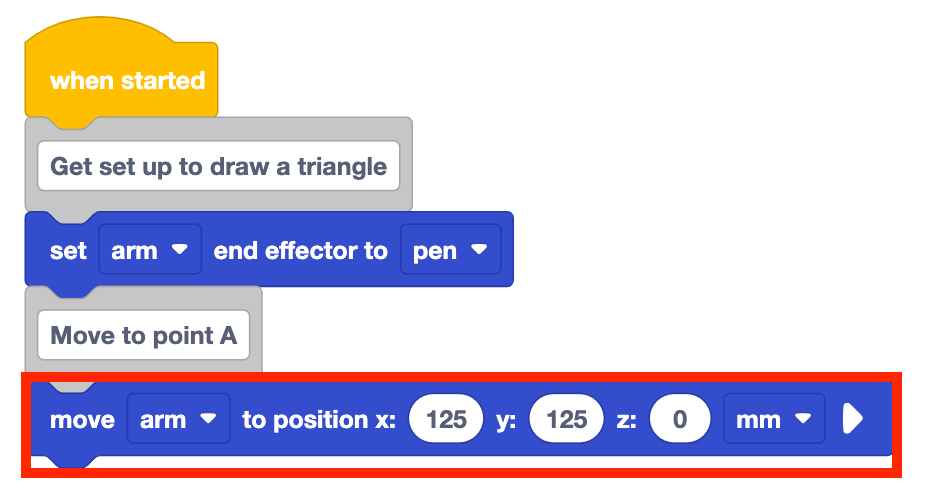
Voeg een Verplaats naar positie blok toe aan de stapel onder het Commentaar blok.

Stel de parameters van op de coördinaten van punt A, zoals vastgelegd in uw technisch notitieboekje.

Voeg opmerkingen toe en Verplaats naar positie blokken voor punten B en C.

Stel de parameters van de blokken Verplaats naar positie in op de coördinaten van de punten B en C, die u in uw technisch notitieboekje hebt genoteerd.

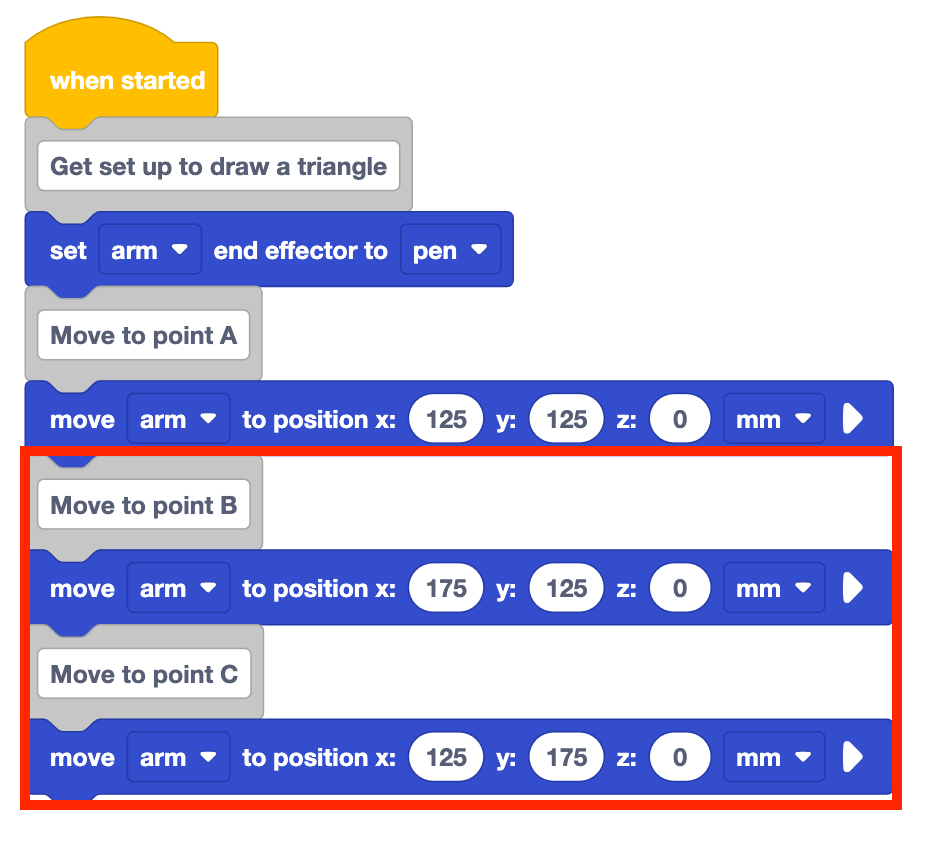
Het project zal in zijn huidige vorm alleen twee zijden van de driehoek tekenen. De 6-assige arm moet terug naar punt A om de driehoek te voltooien.

Voeg een blok met de Comment toe aan de stapel en label het 'Terug naar punt A'. Voeg ook een blok met de waarde Verplaats naar positie toe.

Stel de parameters van de blokken Verplaats naar positie in op de coördinaten van punt A.

Zorg ervoor dat u het project een nieuwe naam geeft en opslaat op uw apparaat.

Zorg ervoor dat de 6-assige arm is aangesloten op VEXcode. Voer uw project uit.

De 6-assige arm begint bij punt A en beweegt vervolgens naar punt B om de eerste zijde van de driehoek te tekenen. Vervolgens gaat de lijn verder naar punt C en tekent de tweede zijde van de driehoek. Vervolgens beweegt de 6-assige arm terug naar punt A om de driehoek te voltooien door de derde zijde te tekenen.

Stop het project zodra de 6-assige arm klaar is met bewegen.

Activiteit

Nu u hebt geleerd hoe u ontbrekende coördinaten kunt vinden als u een begincoördinaat en twee zijdelengtes hebt, kunt u deze vaardigheid gaan oefenen. In deze activiteit borduur je voort op je project uit deze les en ga je een vierkant tekenen.

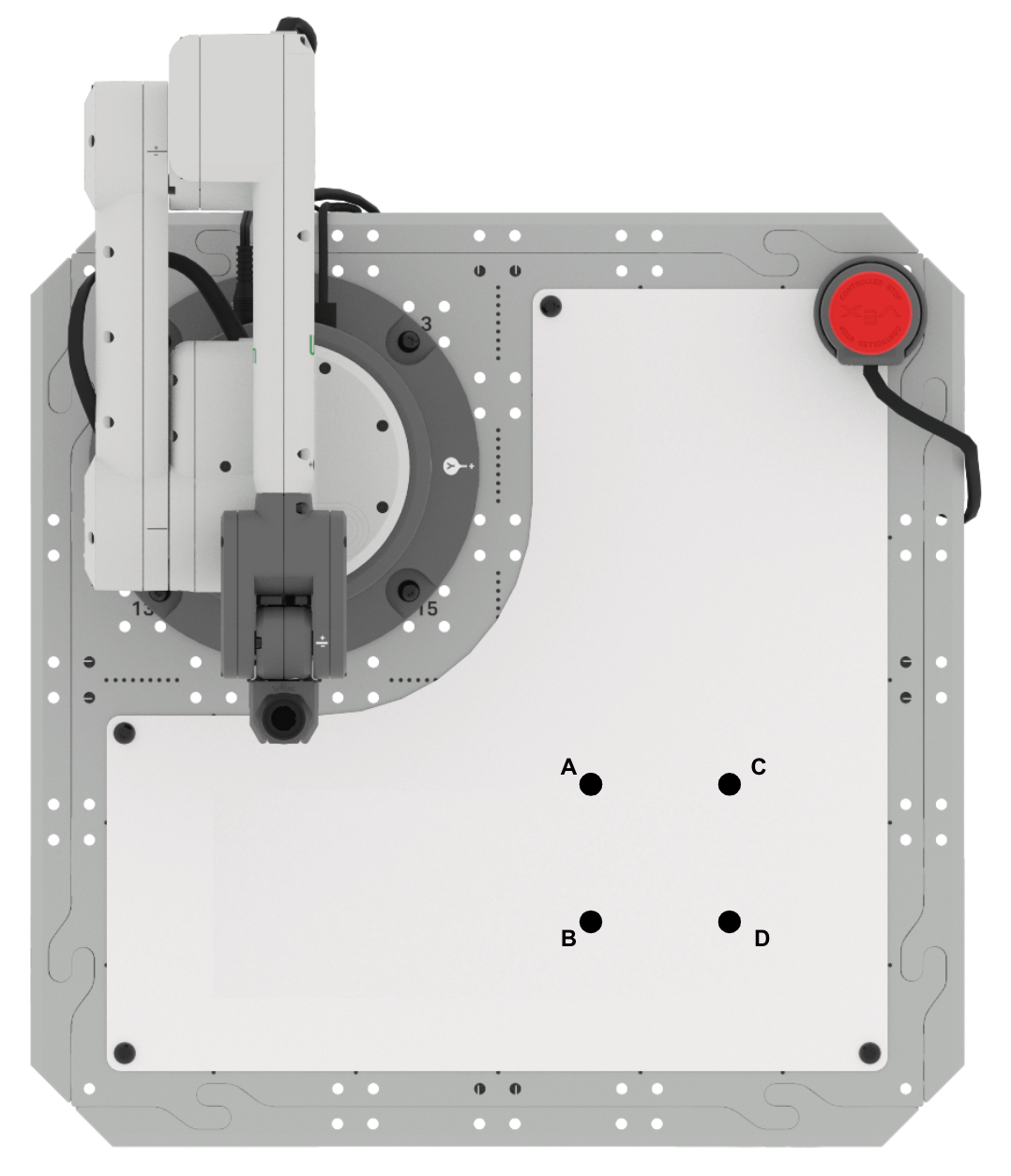
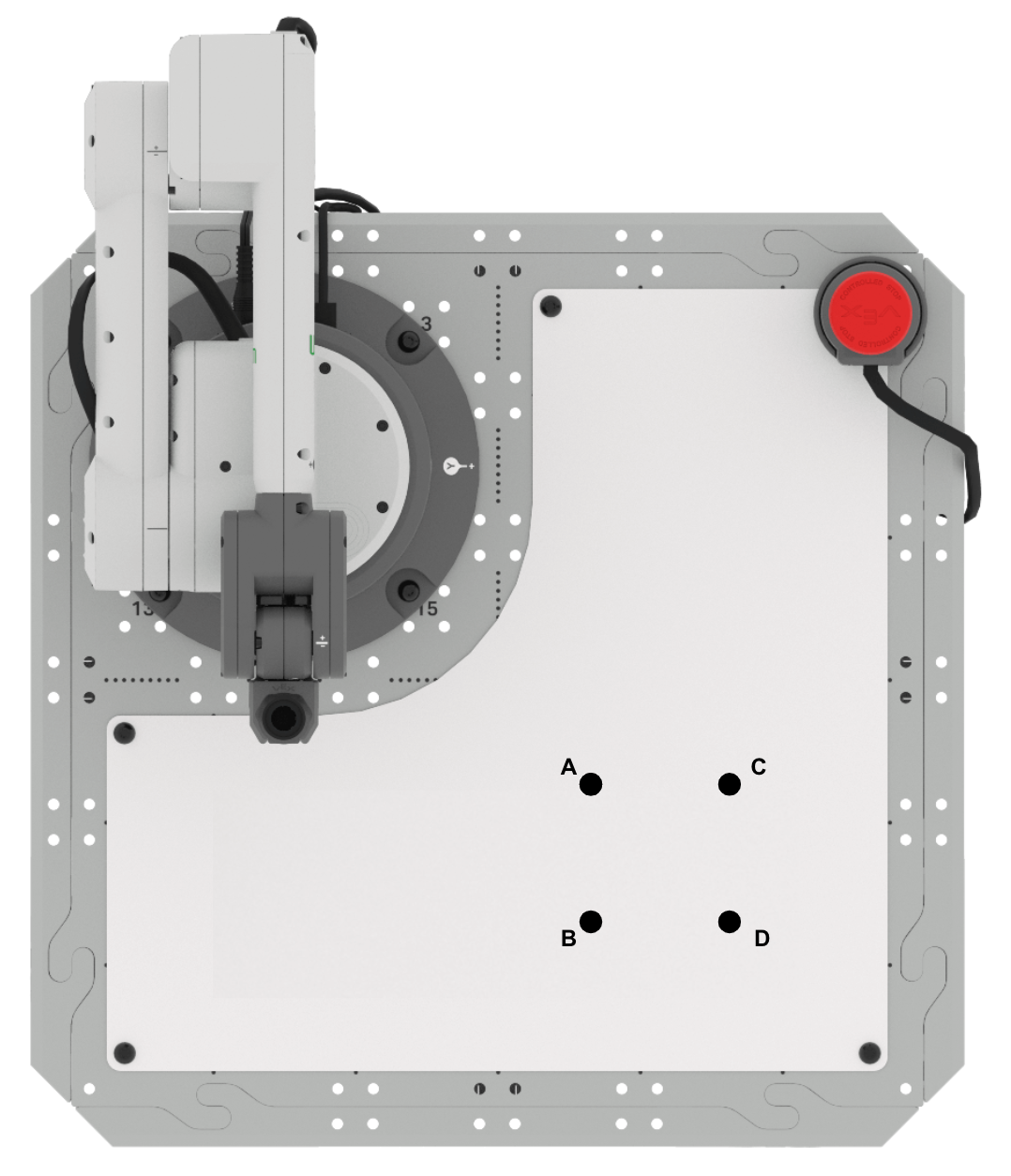
Opstelling: Teken de punten A, B, C en D in je technisch notitieboekje zoals hierboven weergegeven. U kunt de informatie over driehoek ABC uit deze les gebruiken om het ontbrekende punt D te vinden.

Punt A bevindt zich op (125, 125, 0)

Punt B bevindt zich op (175, 125, 0)

Punt C bevindt zich op (125, 175, 0)

Zijlengtes AB en AC zijn 50 mm

Activiteit : Bepaal de coördinaten van punt D. Bouw voort op je project uit deze les om een vierkant te tekenen.

Nadat u uw project hebt bewerkt, kunt u het uitvoeren om te testen. Kan de 6-assige arm alle vier de zijden van het vierkant tekenen? Indien dit niet het geval is, pas dan uw project aan en test het opnieuw.

Noteer het proces dat u gebruikte om punt D te vinden in uw technisch notitieboekje en geef details over hoe u punt D in uw VEXcode-project hebt gebruikt.

Controleer uw begrip

Voordat u doorgaat naar de volgende les, moet u ervoor zorgen dat u de concepten in deze les begrijpt door de vragen in het onderstaande document in uw technische notitieboekje te beantwoorden.

Controleer uw begrip vragen > (Google Doc / .docx / .pdf)

Selecteer Volgende > om te leren hoe u meer driehoeken in verschillende richtingen kunt tekenen.

< Terug Terug naar eenheden Volgende >