In den vorherigen Lektionen haben Sie gelernt, wie Sie mit dem Stifthalter-Tool ein Dreieck auf dem Whiteboard zeichnen, in dem alle Punkte des Dreiecks angegeben wurden. Wenn jedoch einige Punkte des Dreiecks nicht angegeben sind, müssen sie mathematisch bestimmt werden, damit sich der 6-Achsen-Arm in mehreren Achsen bewegen kann.
In dieser Lektion finden Sie zwei fehlende Koordinaten eines Dreiecks, um das Dreieck zu zeichnen. Am Ende dieser Lektion werden Sie das Gelernte auf das Dreieck anwenden, um ein Quadrat zu zeichnen.
Fehlende Koordinaten finden
Der 6-Achsen-Arm wird ein Dreieck zeichnen. Hier sind die Informationen, die wir über dieses Dreieck kennen:
- Punkt A ist (125, 125, 0).
- Jede Seitenlänge beträgt 50 mm.
- Das Dreieck ABC ist ein rechtwinkliges Dreieck (ein Dreieck mit einem 90 ° -Winkel).
- Die diesem Winkel gegenüberliegende Seite ist die längste Seite, bekannt als Hypotenuse. Die anderen beiden Seiten werden als Beine bezeichnet.
Mit diesen Informationen können wir die beiden Endpunkte (Punkte B und C) finden, um das Dreieck zu zeichnen.
Befolgen Sie die folgenden Schritte, um die Punkte B und C zu finden und das Dreieck zu zeichnen.
Befundpunkt B
Zeichnen Sie die bekannten Informationen über das Dreieck in Ihrem technischen Notizbuch.
Punkt A befindet sich bei etwa (125, 125, 0).
Der Abstand von Punkt A zu Punkt B beträgt ca. 50mm. Der Abstand von Punkt A zu Punkt C beträgt ca. 50mm. Jeder dieser Abstände entspricht den Seitenlängen des Dreiecks.
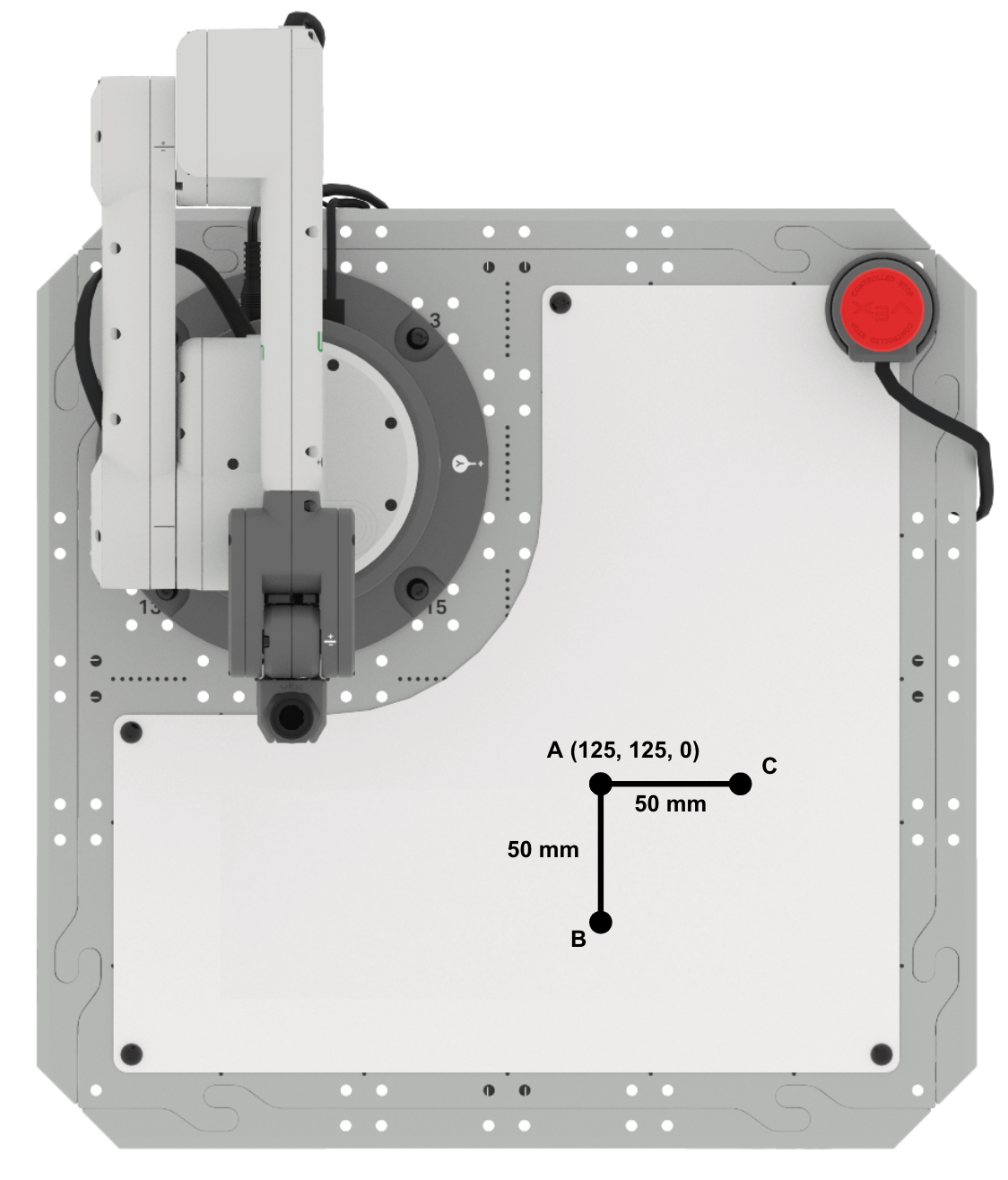
Bestimmen Sie die x-Koordinate von Punkt B. Dies kann durch Addieren der Länge von AB zur x-Koordinate von Punkt A erfolgen, um die x-Koordinate von Punkt B zu finden.
Der x-Wert von Punkt B beträgt 175mm. Notieren Sie dies in Ihrem technischen Notizbuch.
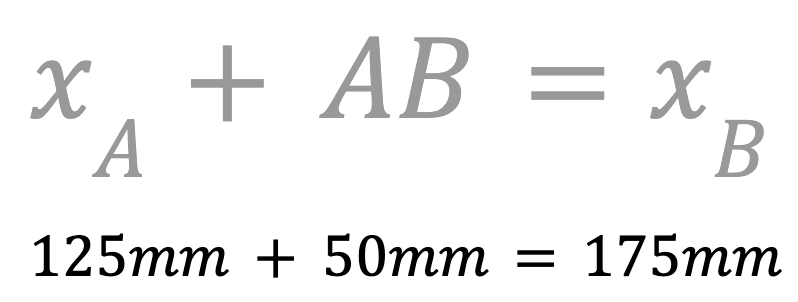
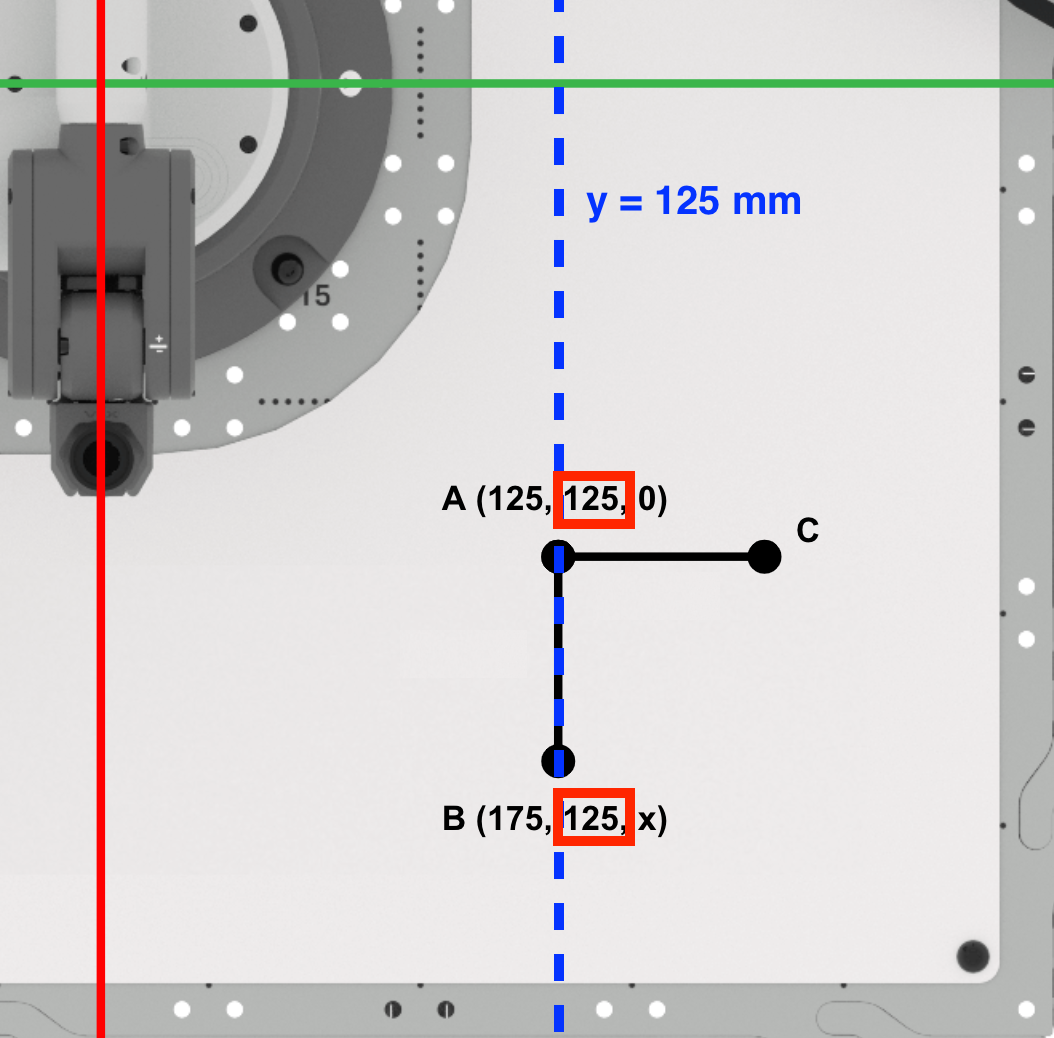
Als nächstes finden wir die y-Koordinate von Punkt B.
Da die Punkte A und B entlang der Linie y=125 mm liegen, ist die y-Koordinate des Punktes B die gleiche wie der Punkt A (125 mm). Notieren Sie dies in Ihrem technischen Notizbuch.
Da sich der Stift nicht zwischen den Punkten A und B hebt, bleibt die z-Koordinate von Punkt B Null.
Punkt B ist (175, 125, 0). Notieren Sie dies in Ihrem technischen Notizbuch.
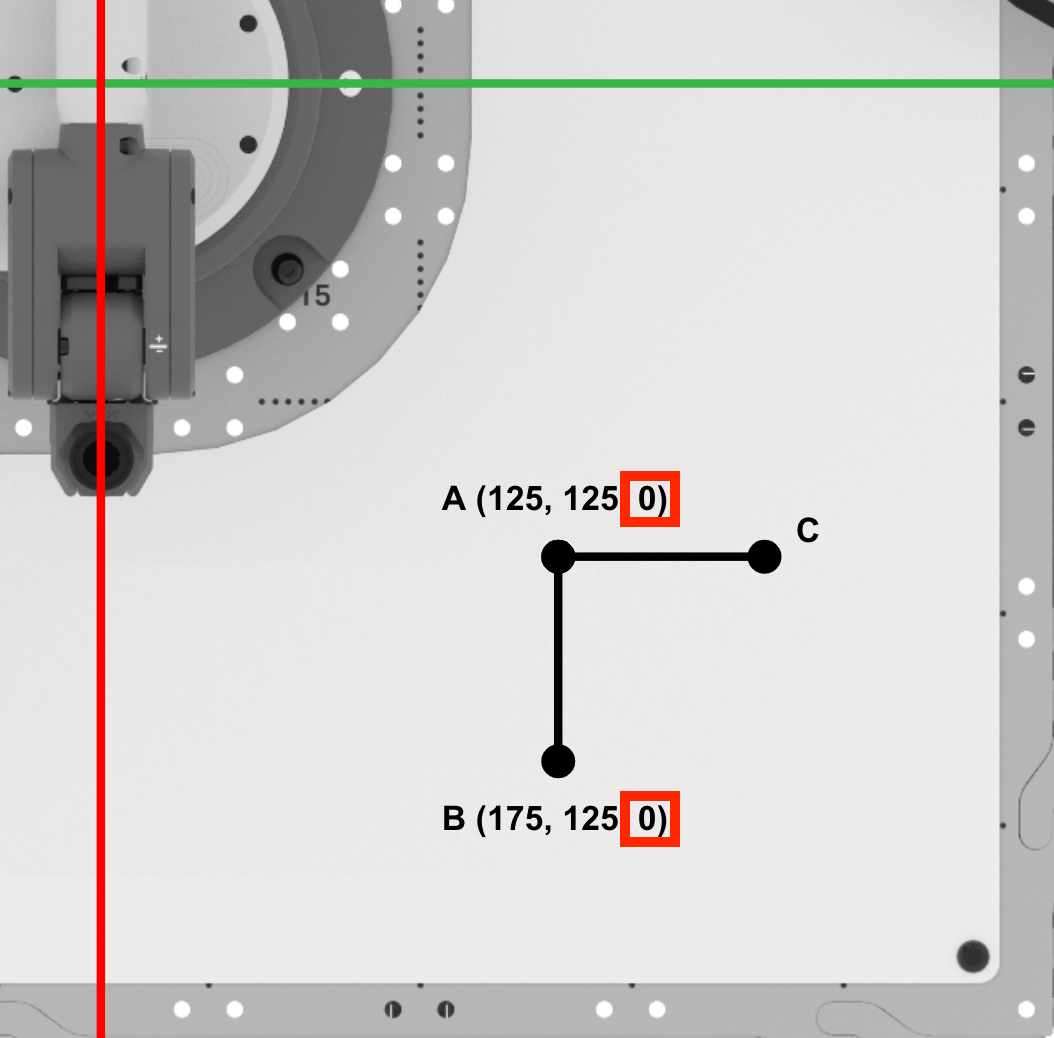
Befundpunkt C
Finde die x-Koordinate von Punkt C.
Da die Punkte A und C entlang der Linie x=125 mm liegen, ist der x-Wert des Punktes C der gleiche wie der Punkt A (125 mm).
Notieren Sie dies in Ihrem technischen Notizbuch.
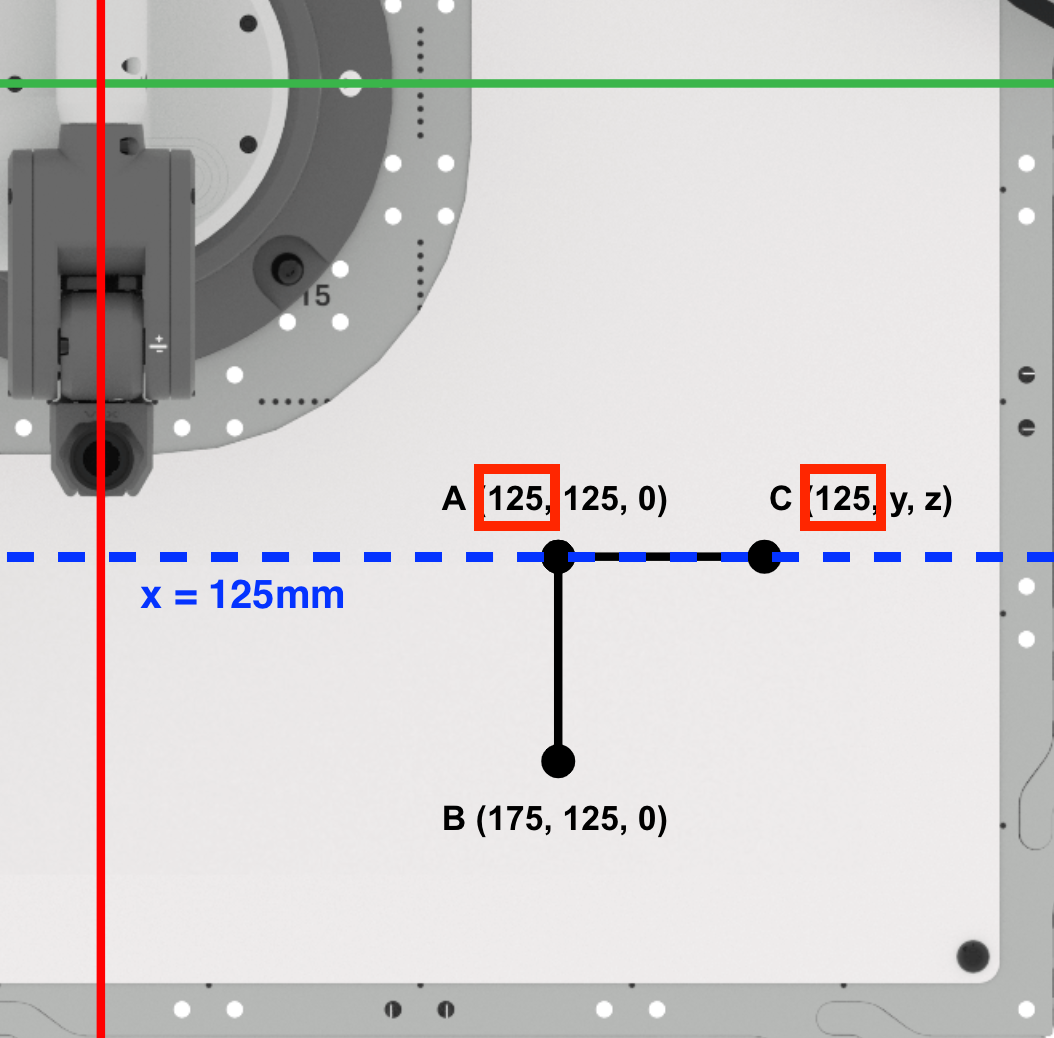
Suchen Sie als Nächstes die y-Koordinate von Punkt C.
Da wir ein rechtwinkliges Dreieck zeichnen, wissen wir, dass die AC-Seite parallel zur y-Achse verläuft. Addieren Sie die Länge von AC zur y-Koordinate von Punkt A, um die y-Koordinate von Punkt C zu finden.
Die y-Koordinate des Punktes C beträgt 175 mm. Notieren Sie dies in Ihrem technischen Notizbuch.
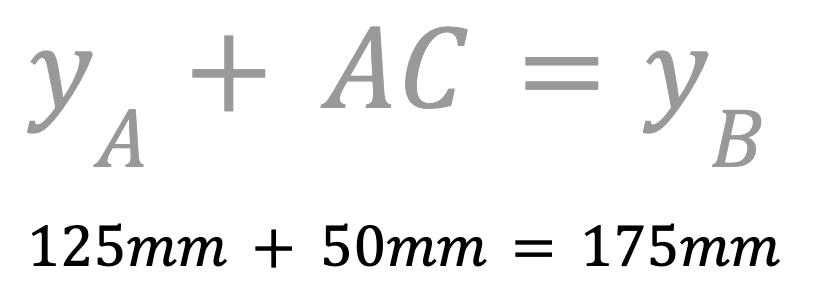
Da sich der Stift nicht zwischen den Punkten A und C hebt, bleibt die z-Koordinate des Punktes C Null.
Punkt C ist (125, 175, 0). Notieren Sie dies in Ihrem technischen Notizbuch.
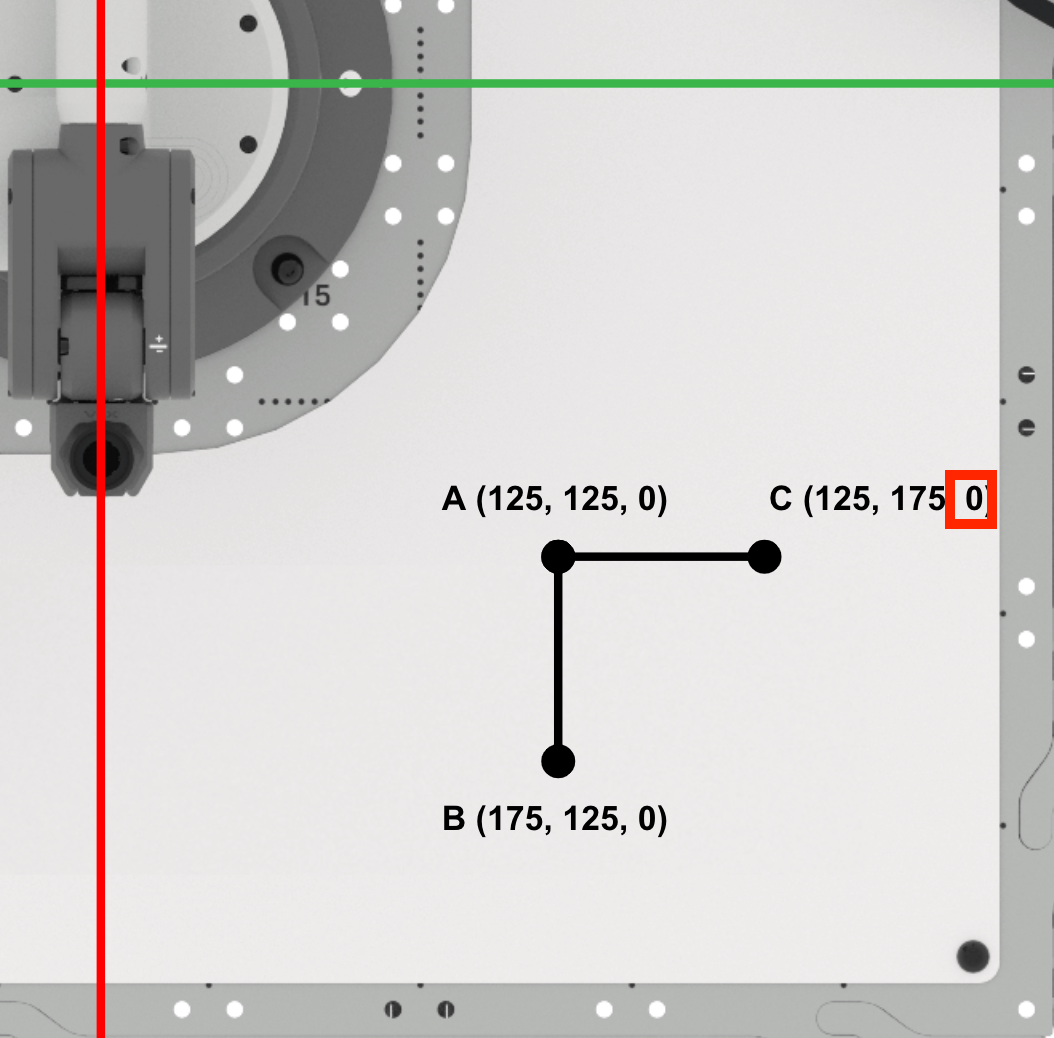
Codierung des 6-Achsen-Arms zur Verbindung der Punkte A, B und C
Nachdem Sie nun die Koordinaten für die Punkte B und C bestimmt haben, ist es an der Zeit, ein VEXcode EXP-Projekt für den 6-Achsen-Arm zu erstellen, um die Punkte A, B und C zu verbinden, um ein Dreieck zu zeichnen.
Öffnen Sie ein neues Blockprojekt, indem Sie den Schritten in diesem Video folgen.
Fügen Sie dem Stapel einen Kommentarblock hinzu und geben Sie "Einrichten, um ein Dreieck zu zeichnen" ein.
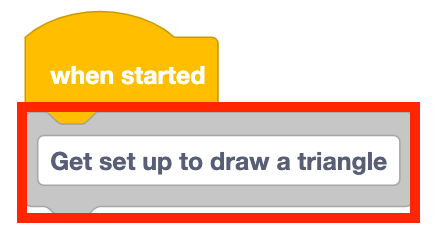
Fügen Sie dem Stapel einen Set-Endeffektorblock hinzu und setzen Sie ihn auf "Stift".

Fügen Sie dem Stapel einen Kommentarblock hinzu und geben Sie "Zu Punkt A verschieben" ein.
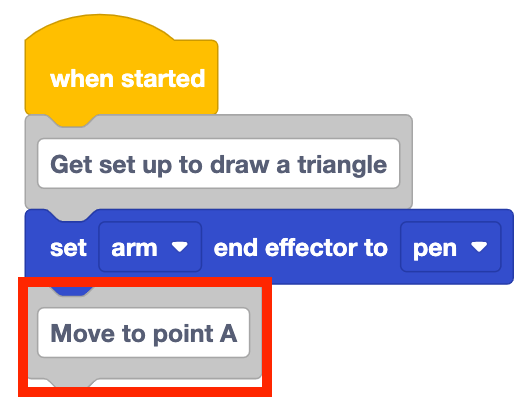
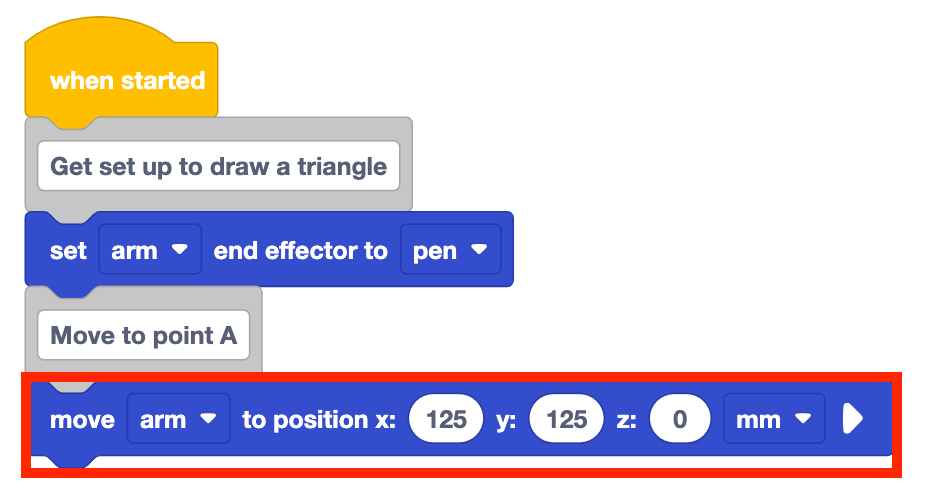
Fügen Sie dem Stapel unter dem Kommentarblock einen Verschieben-zu-Position-Block hinzu.
Legen Sie die Parameter des Bewegungsblocks auf die Koordinaten von Punkt A fest, die in Ihrem technischen Notizbuch dokumentiert sind.
Kommentar hinzufügen und zu den Positionsblöcken für die Punkte B und C verschieben.
Legen Sie die Parameter der Blöcke zum Positionieren bewegen auf die Koordinaten der Punkte B und C fest, die in Ihrem technischen Notizbuch aufgezeichnet wurden.
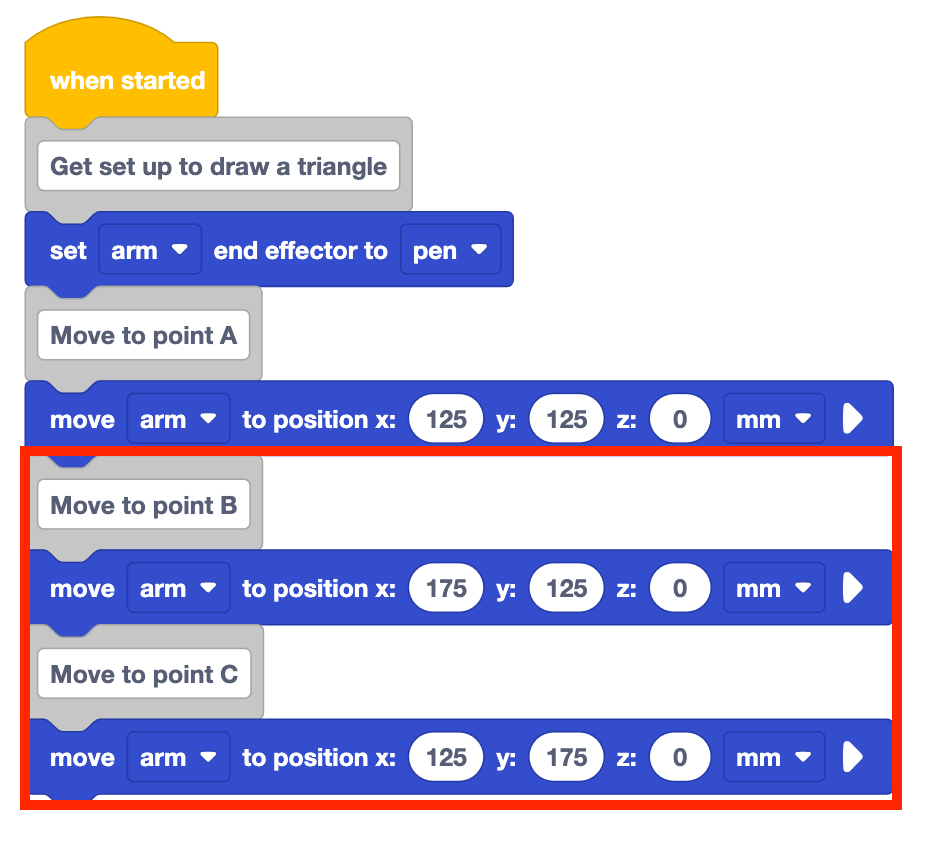
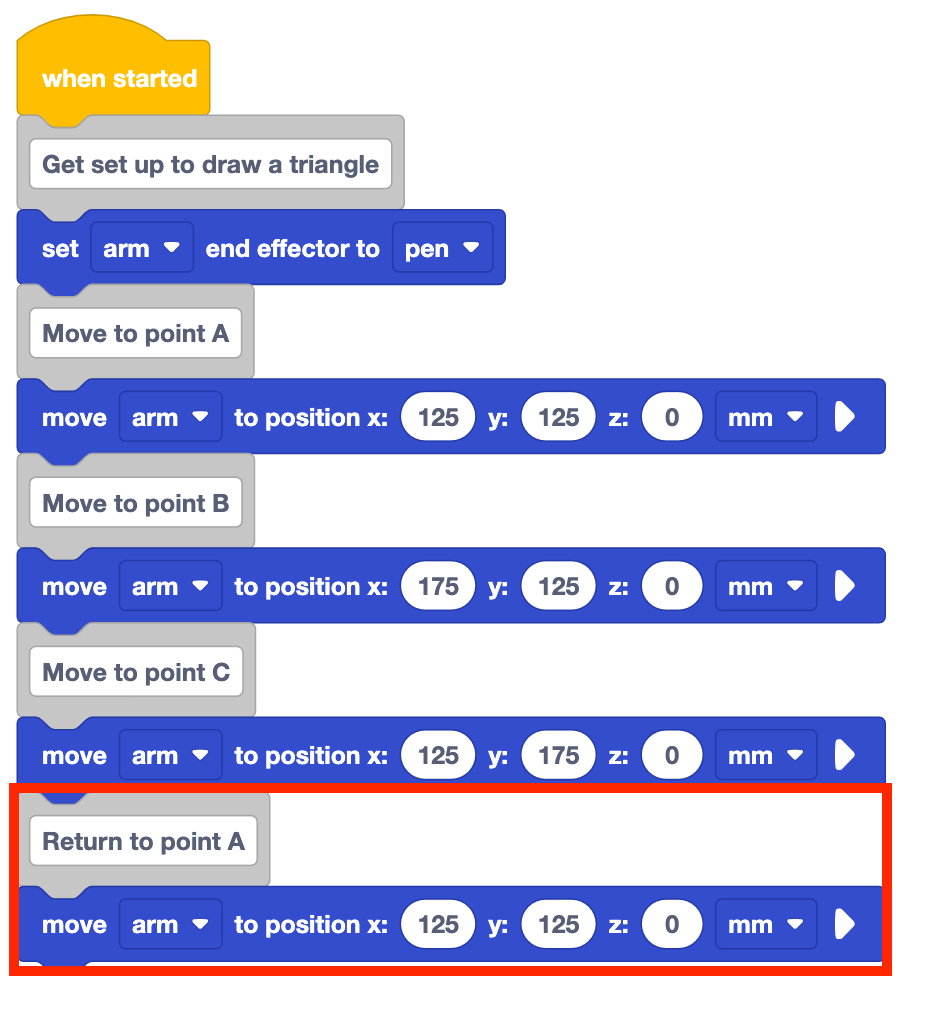
Das Projekt wie es ist, wird nur zwei Seiten des Dreiecks zeichnen. Der 6-Achsen-Arm muss zurück zu Punkt A gehen, um das Dreieck zu vervollständigen.
Fügen Sie dem Stapel einen Kommentarblock hinzu und beschriften Sie ihn mit "Zurück zu Punkt A" sowie mit einem Verschieben zu Positionsblock.
Legen Sie die Parameter der Position der Blöcke auf die Koordinaten des Punktes A fest.
Achten Sie darauf, Ihr Projekt umzubenennen und auf Ihrem Gerät zu speichern.

Stellen Sie sicher, dass der 6-Achsen-Arm mit dem VEXcode verbunden ist. Führen Sie Ihr Projekt aus.
Der 6-Achsen-Arm beginnt an Punkt A und bewegt sich dann zu Punkt B, um die erste Seite des Dreiecks zu zeichnen. Er fährt dann mit Punkt C fort und zeichnet die zweite Seite des Dreiecks. Der 6-Achsen-Arm bewegt sich dann zurück zu Punkt A, um das Dreieck zu vervollständigen, indem die dritte Seite gezeichnet wird.
Stoppen Sie das Projekt, sobald der 6-Achsen-Arm seine Bewegung beendet hat.

Aktivität
Nachdem Sie nun gelernt haben, fehlende Koordinaten bei einer Anfangskoordinate und zwei Seitenlängen zu finden, werden Sie diese Fertigkeit üben. In dieser Aktivität bauen Sie auf Ihrem Projekt aus dieser Lektion auf, um ein Quadrat zu zeichnen.
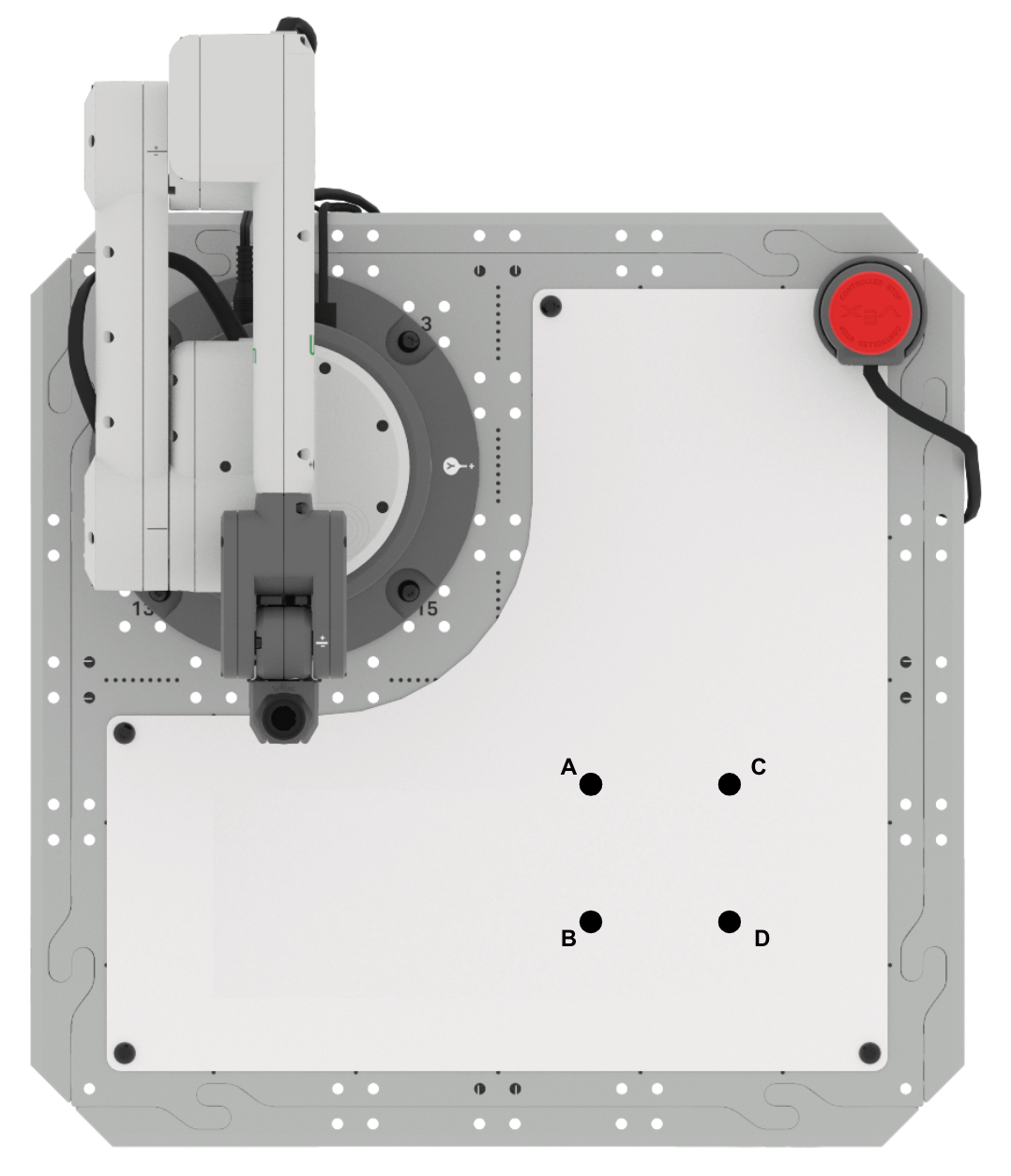
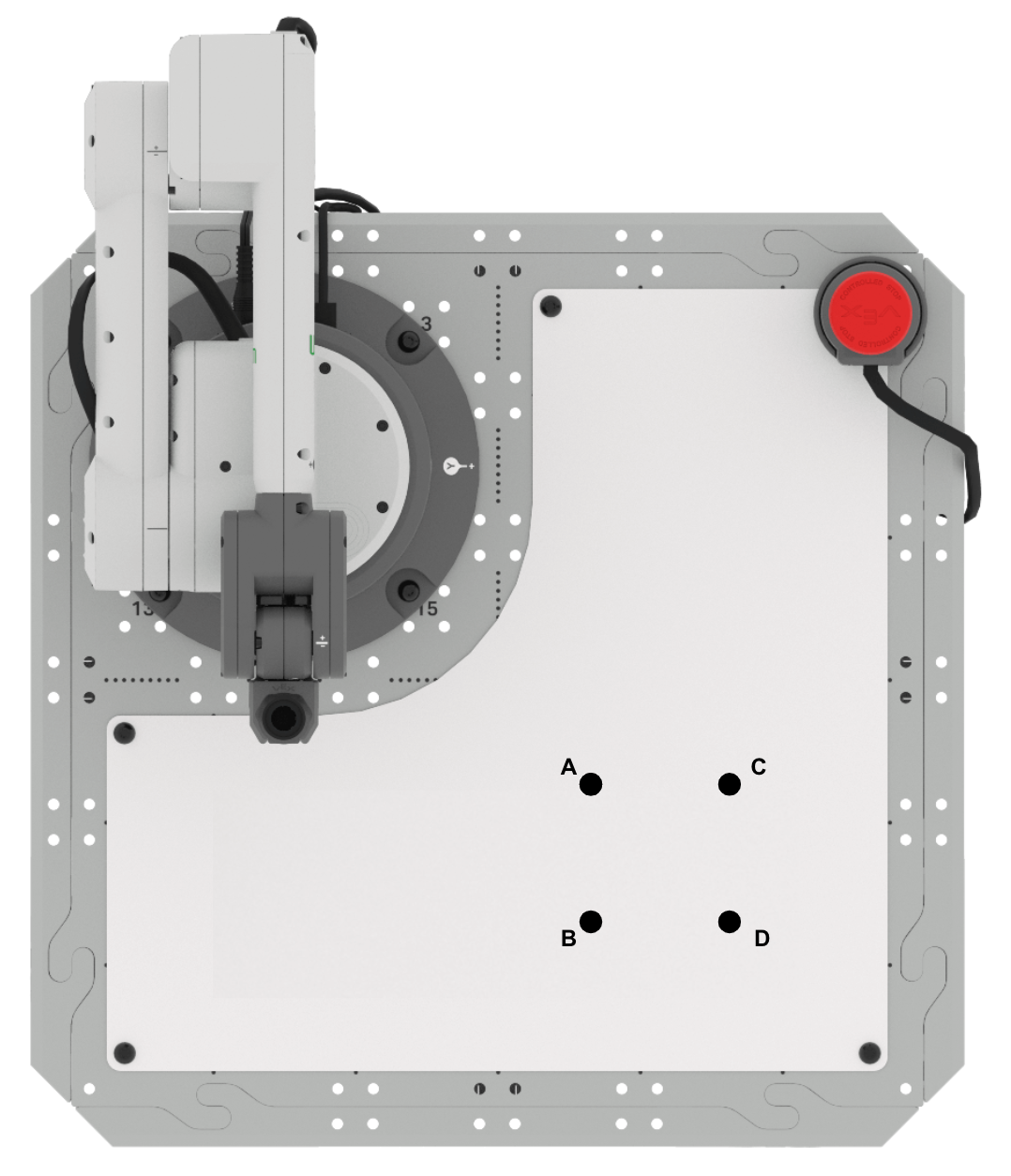
- Setup: Zeichnen Sie die Punkte A, B, C und D in Ihrem technischen
Notizbuch wie oben gezeigt. Sie können die Informationen über das Dreieck ABC aus dieser
Lektion verwenden, um den fehlenden Punkt D zu finden.
- Punkt A befindet sich bei (125, 125, 0)
- Punkt B befindet sich bei (175, 125, 0)
- Punkt C befindet sich bei (125, 175, 0)
- Seitenlängen AB und AC sind 50mm
- Aktivität: Finde die Koordinaten von Punkt D. Baue aus dieser Lektion
auf dein Projekt auf, um ein Quadrat zu zeichnen.
- Sobald Sie Ihr Projekt bearbeitet haben, führen Sie es zum Testen aus. Zeichnet der 6-Achsen-Arm erfolgreich alle vier Seiten des Quadrats? Wenn nicht, ändern Sie Ihr Projekt und testen Sie es erneut.
- Notieren Sie den Prozess, mit dem Sie Punkt D in Ihrem technischen Notizbuch gefunden haben, und fügen Sie Details darüber ein, wie Sie Punkt D in Ihrem VEXcode-Projekt verwendet haben.
Überprüfe dein Verständnis
Bevor Sie mit der nächsten Lektion fortfahren, stellen Sie sicher, dass Sie die Konzepte in dieser Lektion verstehen, indem Sie die Fragen im folgenden Dokument in Ihrem technischen Notizbuch beantworten.
Fragen zum Verständnis prüfen > (Google Doc / .docx / .pdf)
Wählen Sie Weiter > , um zu erfahren, wie Sie mehr Dreiecke in verschiedenen Ausrichtungen zeichnen können.