En las lecciones anteriores, aprendiste a dibujar un triángulo en la pizarra con la herramienta Portaplumas donde se daban todos los puntos del triángulo. Sin embargo, si no se dan algunos puntos del triángulo, deberán determinarse matemáticamente para que el brazo de 6 ejes se mueva en múltiples ejes.
En esta lección, encontrarás dos coordenadas faltantes de un triángulo para dibujarlo. Al final de esta lección, aplicarás lo que has aprendido a construir en el triángulo para dibujar un cuadrado.
Encontrar coordenadas faltantes
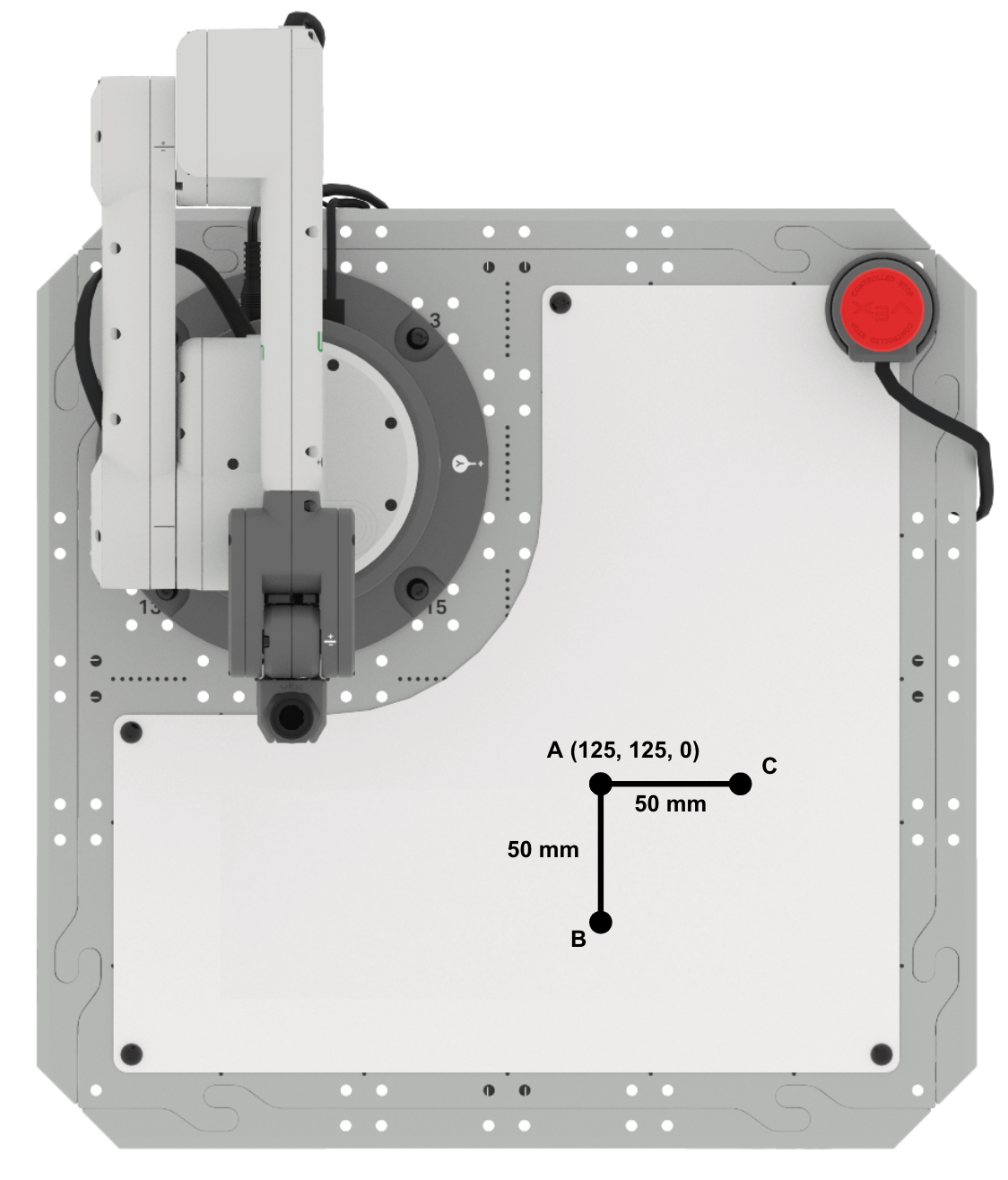
El brazo de 6 ejes va a dibujar un triángulo. Esta es la información que conocemos sobre este triángulo:
- El punto A es (125, 125, 0).
- Cada lado tiene una longitud de 50 mm.
- El triángulo ABC es un triángulo rectángulo (un triángulo con un ángulo de 90 º).
- El lado opuesto a este ángulo es el lado más largo, conocido como hipotenusa. Los otros dos lados se llaman patas.
Usando esta información, podemos encontrar los dos puntos finales (puntos B y C) para dibujar el triángulo.
Sigue los pasos a continuación para encontrar los puntos B y C y dibuja el triángulo.
Encontrar el punto B
Dibuja la información conocida sobre el triángulo en tu cuaderno de ingeniería.
El punto A se encuentra aproximadamente en (125, 125, 0).
La distancia del punto A al punto B es de aproximadamente 50 mm. La distancia del punto A al punto C es de aproximadamente 50 mm. Cada una de estas distancias corresponde a las longitudes laterales del triángulo.
Determine la coordenada x del punto B. Esto se puede hacer sumando la longitud de AB a la coordenada x del punto A para encontrar la coordenada x del punto B.
El valor x del punto B es 175 mm. Registre esto en su cuaderno de ingeniería.
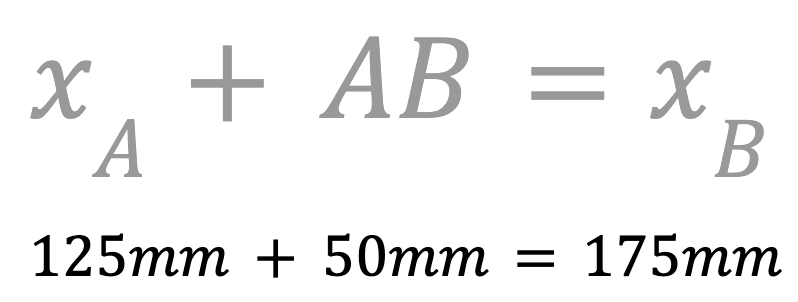
A continuación, encontraremos la coordenada y del punto B.
Dado que los puntos A y B están a lo largo de la línea y=125 mm, la coordenada y del punto B es la misma que la del punto A (125 mm). Registre esto en su cuaderno de ingeniería.
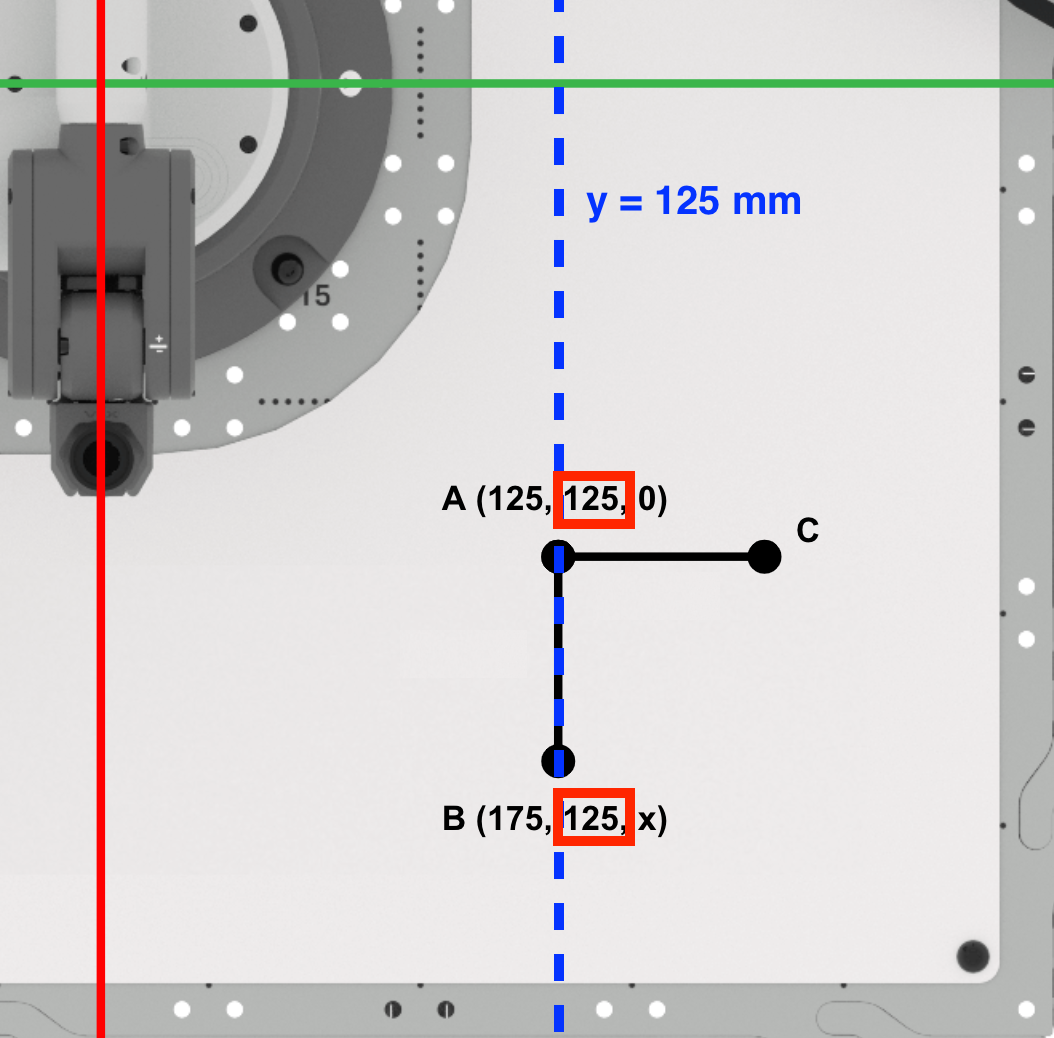
Dado que la pluma no se eleva entre los puntos A y B, la coordenada z del punto B seguirá siendo cero.
El punto B es (175, 125, 0). Registre esto en su cuaderno de ingeniería.
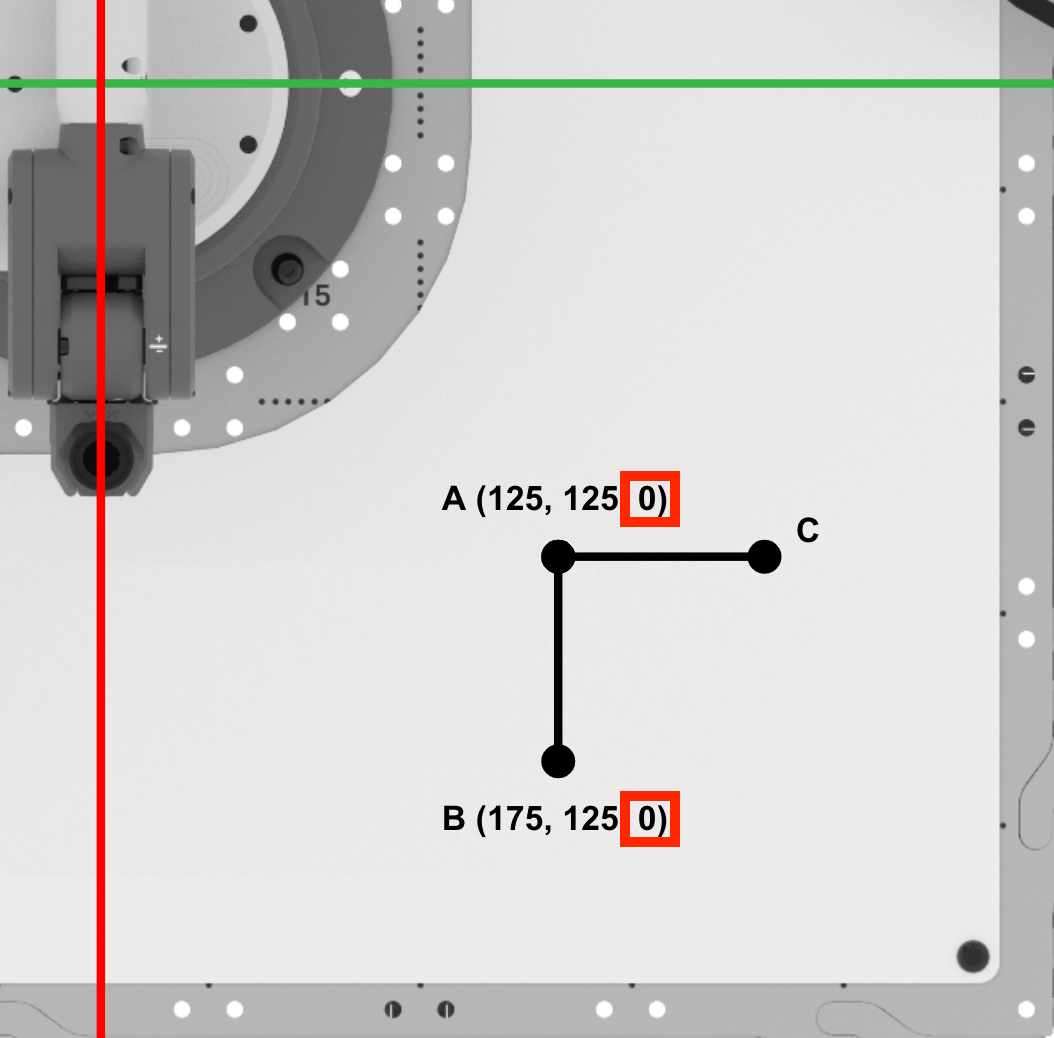
Encontrar el punto C
Halla la coordenada x del punto C.
Dado que los puntos A y C están a lo largo de la línea x=125 mm, el valor x del punto C es el mismo que el punto A (125 mm).
Registre esto en su cuaderno de ingeniería.
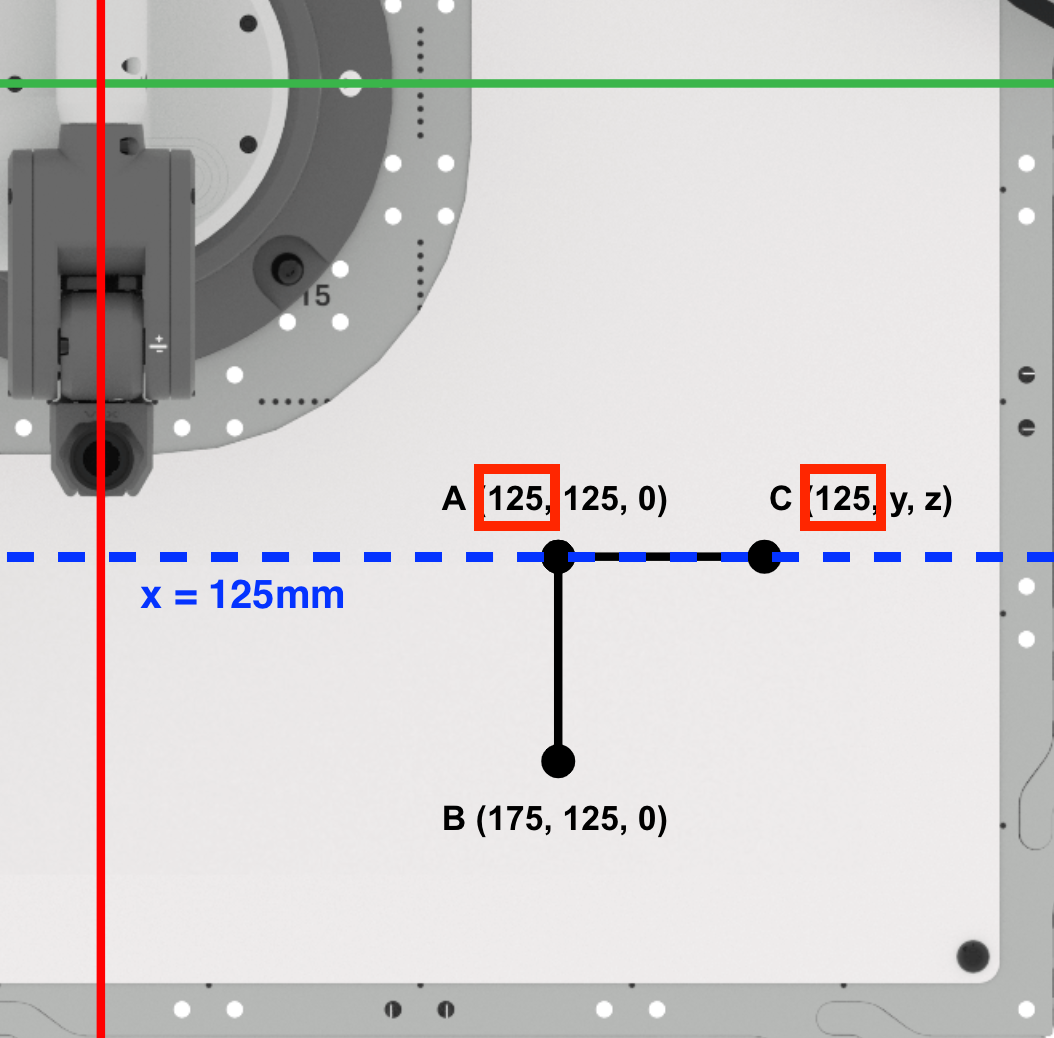
A continuación, encuentre la coordenada y del punto C.
Dado que estamos dibujando un triángulo rectángulo, sabemos que el lado AC será paralelo al eje y. Sume la longitud de AC a la coordenada y del punto A para encontrar la coordenada y del punto C.
La coordenada y del punto C es 175 mm. Registre esto en su cuaderno de ingeniería.
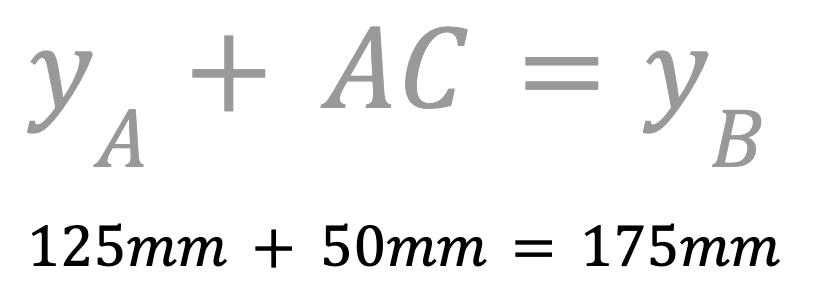
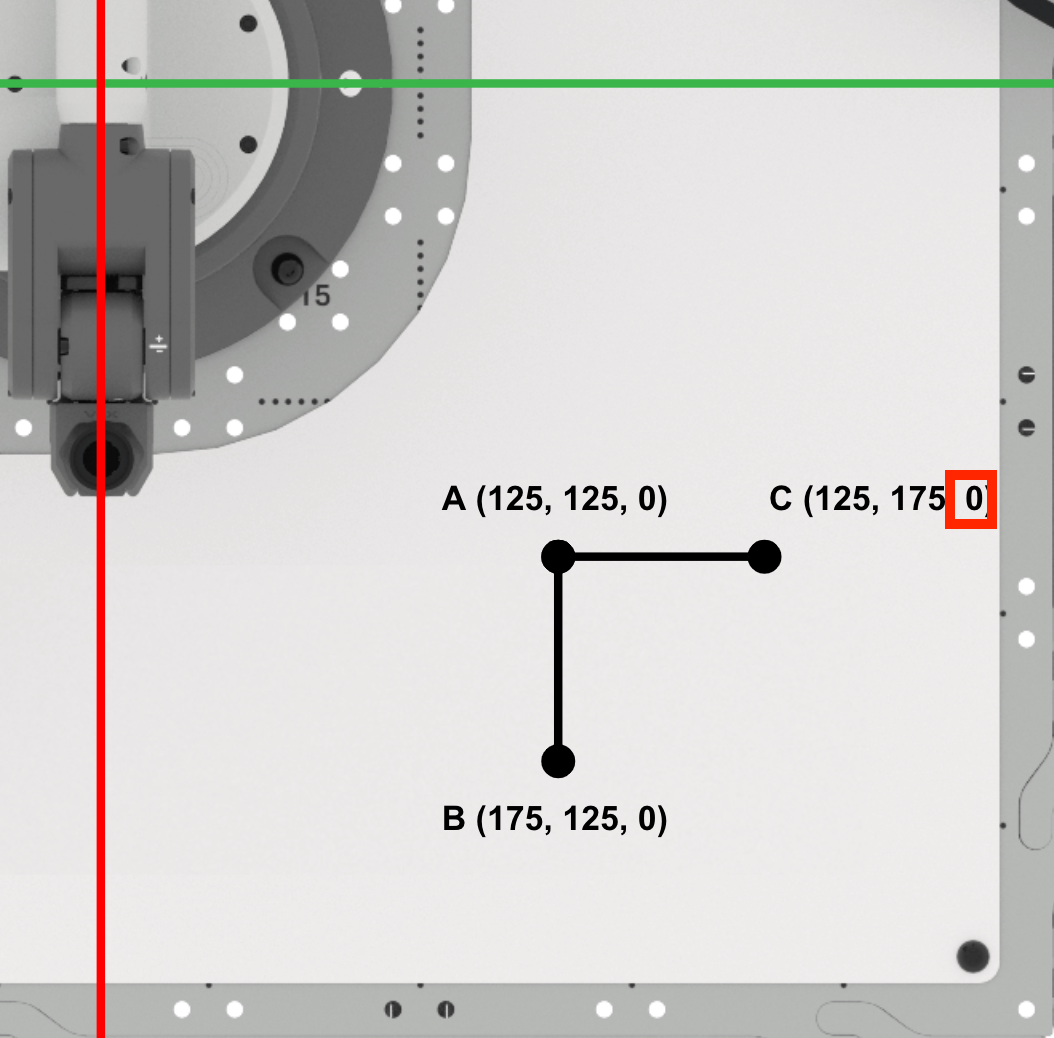
Dado que la pluma no se eleva entre los puntos A y C, la coordenada z del punto C seguirá siendo cero.
El punto C es (125, 175, 0). Registre esto en su cuaderno de ingeniería.
Codificación del brazo de 6 ejes para conectar los puntos A, B y C
Ahora que ha determinado las coordenadas para los puntos B y C, es hora de crear un proyecto VEXcode EXP para que el brazo de 6 ejes conecte los puntos A, B y C para dibujar un triángulo.
Abra un proyecto de nuevos bloques siguiendo los pasos de este vídeo.
Añade un bloque de comentarios a la pila y escribe 'Prepárate para dibujar un triángulo'.
Añada un bloque Set end efector a la pila y ajústelo a 'pen'.

Añade un bloque de comentarios a la pila y escribe "Mover al punto A".
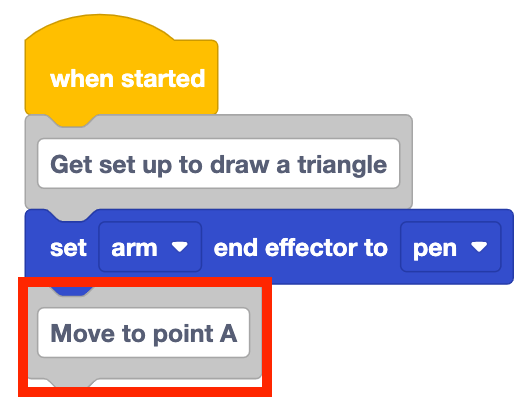
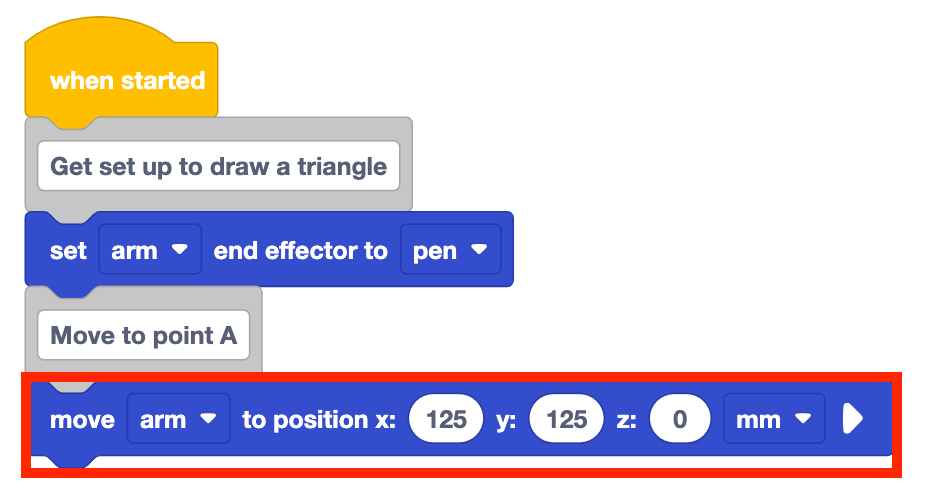
Añada un bloque Mover a posición a la pila debajo del bloque Comentario.
Establezca los parámetros del bloque Mover a posición en las coordenadas del punto A, documentadas en su cuaderno de ingeniería.
Añadir comentario y mover a los bloques de posición para los puntos B y C.
Establezca los parámetros de los bloques Move to position en las coordenadas de los puntos B y C, que se registraron en su cuaderno de ingeniería.
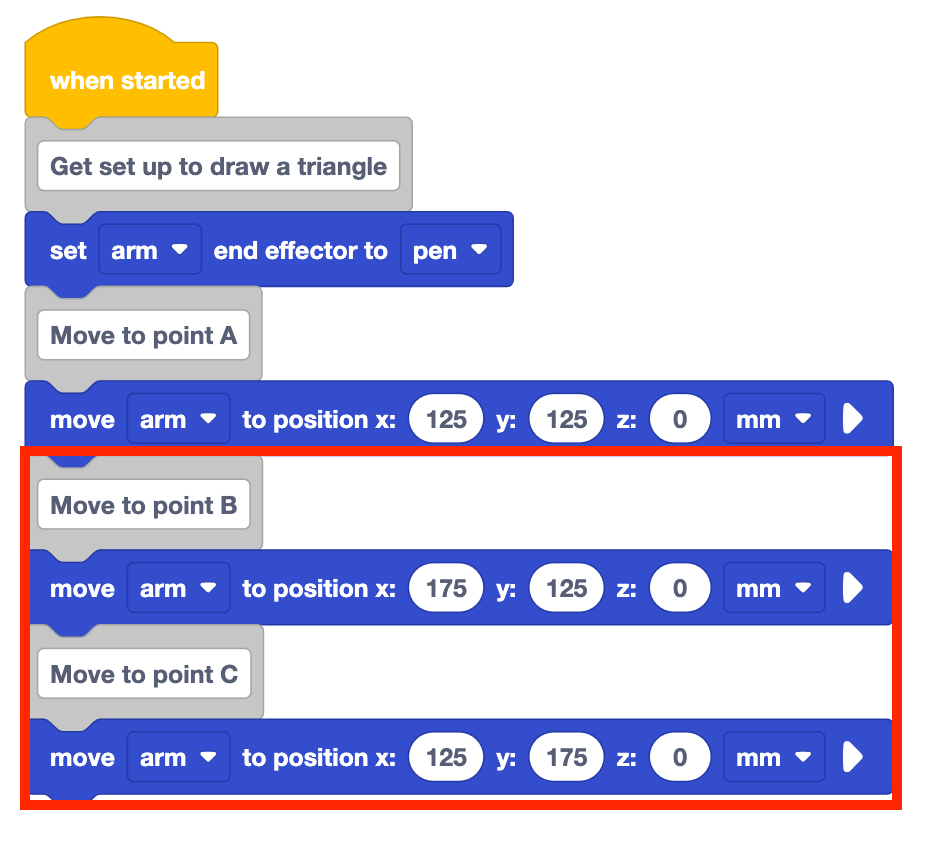
El proyecto tal como está solo dibujará dos lados del triángulo. El brazo de 6 ejes debe volver al punto A para completar el triángulo.
Añada un bloque de comentarios a la pila y etiquételo 'Volver al punto A', así como añada un bloque Mover a la posición.
Establezca los parámetros de los bloques Move to position en las coordenadas del punto A.
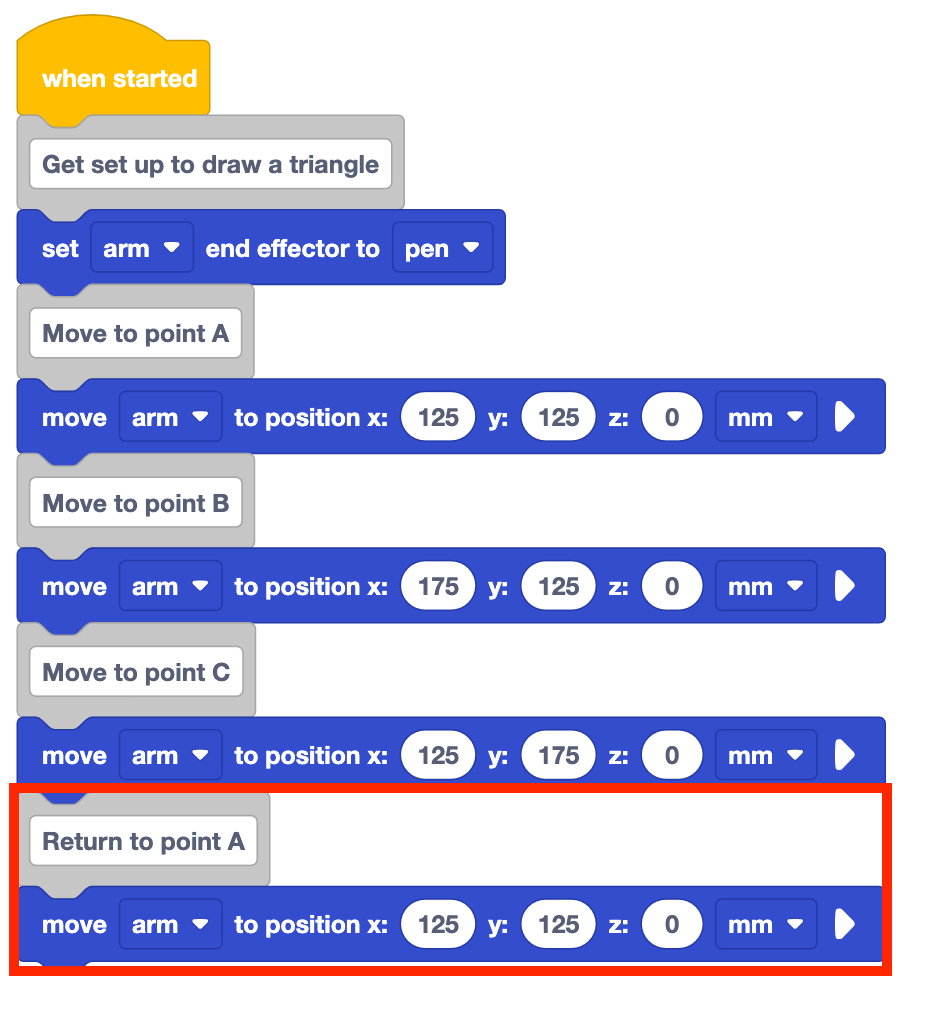
Asegúrese de cambiar el nombre y guardar su proyecto en su dispositivo.

Asegúrese de que el brazo de 6 ejes esté conectado a VEXcode. Ejecuta tu proyecto.
El brazo de 6 ejes comenzará en el punto A, luego se moverá al punto B para dibujar el primer lado del triángulo. Luego continuará hasta el punto C, dibujando el segundo lado del triángulo. El brazo de 6 ejes se moverá hacia atrás al punto A para completar el triángulo dibujando el tercer lado.
Detenga el proyecto una vez que el brazo de 6 ejes haya terminado de moverse.

Actividad
Ahora que has aprendido a encontrar las coordenadas que faltan dada una coordenada inicial y dos longitudes laterales, practicarás esta habilidad. En esta actividad, aprovecharás tu proyecto de esta lección para dibujar un cuadrado.
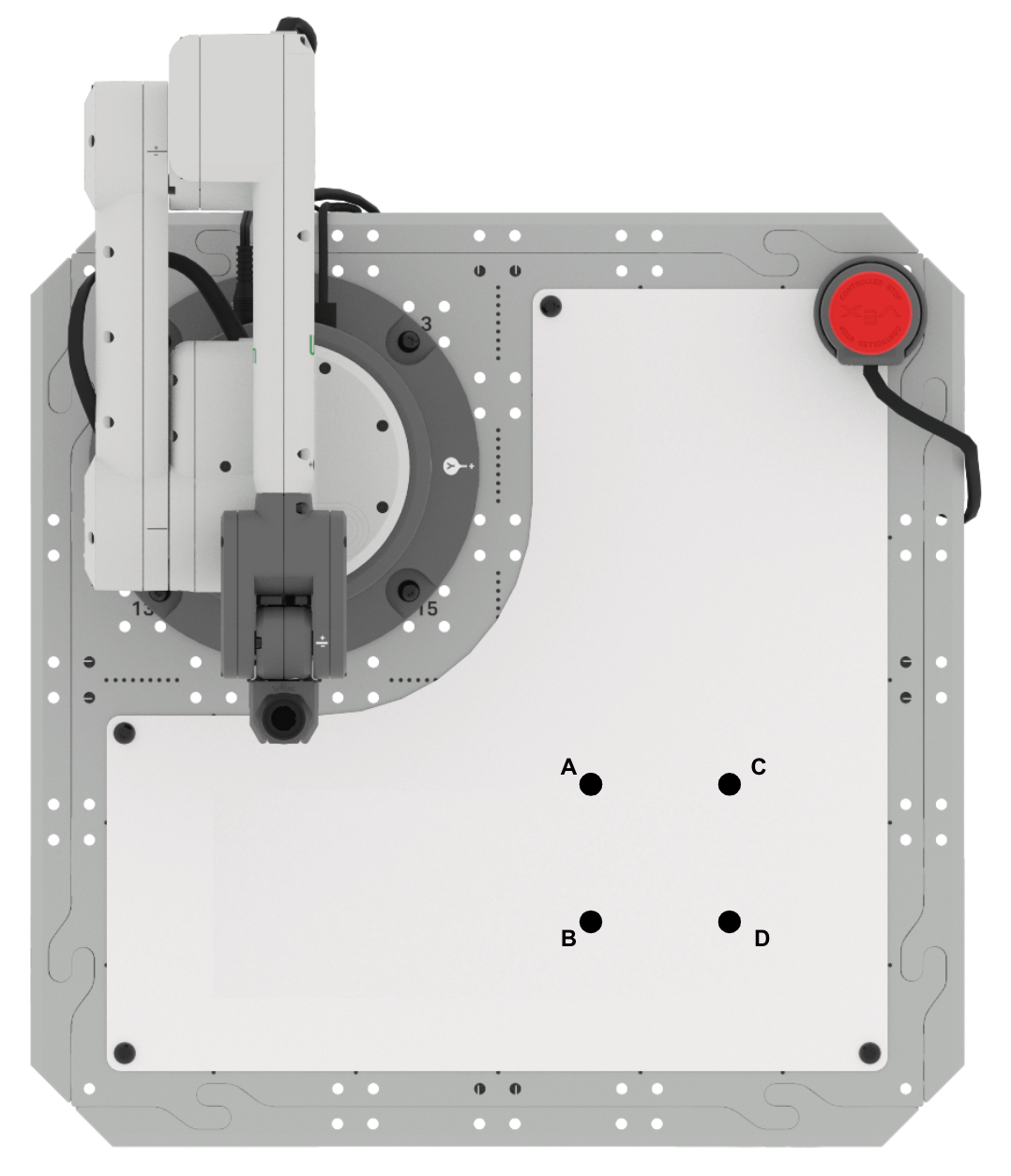
- Configuración: dibuje los puntos A, B, C y D en su cuaderno de
ingeniería como se muestra arriba. Puedes usar la información sobre el triángulo ABC de
esta lección para ayudarte a encontrar el punto D que falta.
- El punto A se encuentra en (125, 125, 0)
- El punto B se encuentra en (175, 125, 0)
- El punto C se encuentra en (125, 175, 0)
- Las longitudes laterales AB y AC son de 50 mm
- Actividad: Encuentre las coordenadas del punto D. Construya
su proyecto a partir de esta Lección para dibujar un cuadrado.
- Una vez que hayas editado tu proyecto, ejecútalo para probarlo. ¿El brazo de 6 ejes dibuja con éxito los cuatro lados del cuadrado? Si no es así, modifique su proyecto y pruébelo de nuevo.
- Registre el proceso que utilizó para encontrar el punto D en su cuaderno de ingeniería e incluya detalles sobre cómo utilizó el punto D en su proyecto VEXcode.
Compruebe su comprensión
Antes de pasar a la siguiente lección, asegúrate de comprender los conceptos de esta lección respondiendo las preguntas del siguiente documento en tu cuaderno de ingeniería.
Verifique sus preguntas de comprensión > (Google Doc / .docx / .pdf)
Selecciona Siguiente > para aprender a dibujar más triángulos en diferentes orientaciones.