In der vorherigen Einheit haben Sie den 6-Achsen-Arm zu verschiedenen Wegpunkten um ein Hindernis bewegt, indem Sie sich einzeln entlang der x- und y-Achse bewegt haben. In dieser Einheit werden Sie darauf aufbauen, um Bewegungen entlang mehrerer Achsen gleichzeitig zu integrieren. Mit dem Stift können Sie den Weg des 6-Achsen-Arms sehen, während er Formen mit diagonalen Linien wie ein Dreieck zeichnet.
In dieser Lektion wirst du:
- Erfahren Sie mehr über die mehrachsige Bewegung in Bezug auf den 6-Achsen-Arm.
- Schauen Sie sich ein Projekt an und prognostizieren Sie die Bewegung des 6-Achsen-Arms.
- Vergleichen Sie Ihre Vorhersage mit der tatsächlichen Bewegung des 6-Achsen-Arms.
Bewegen entlang mehrerer Achsen
Wenn du den 6-Achsen-Arm codiert hast, um dich zu verschiedenen Wegpunkten in der vorherigen
Einheit zu bewegen, hast du dich einzeln entlang der x- und y-Achse bewegt. Dies war
wichtig, damit Sie sich an den vorhandenen Hindernissen bewegen können. 
Es ist jedoch wichtig zu beachten, dass dies nicht immer der schnellste Weg ist, um von einem Punkt zum anderen zu gelangen. Wenn sich im obigen Bild kein Hindernis befindet, können Sie sich direkt von Punkt 1 zu Punkt 3 bewegen, indem Sie sich diagonal bewegen.
Dazu müsste sich der 6-Achsen-Arm gleichzeitig auf der x- und der y-Achse bewegen. In dieser Lektion werden Sie sich ein Projekt ansehen, das darauf abzielt, den 6-Achsen-Arm entlang mehrerer Achsen zu bewegen, um besser zu verstehen, wie sich der 6-Achsen-Arm im 3D-Raum bewegt.
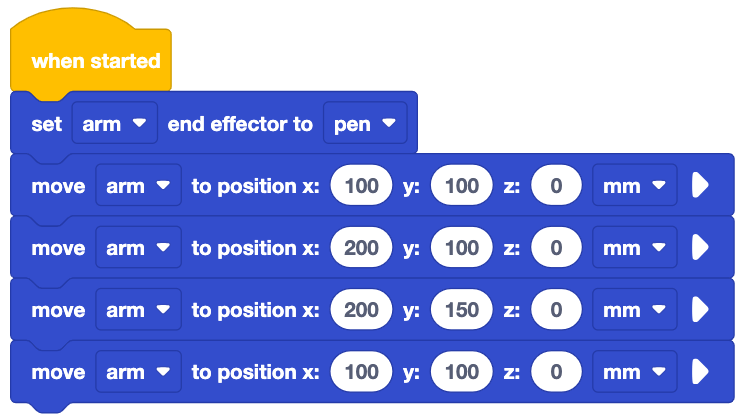
Schauen Sie sich die Blöcke in diesem Projekt an. Denken Sie darüber nach, was Sie über die Bewegungen des 6-Achsen-Arms gelernt haben. Was wird der 6-Achsen-Arm Ihrer Meinung nach tun, wenn dieses Projekt ausgeführt wird?
Notieren Sie Ihre Vorhersage in Ihrem technischen Notizbuch. Beschreiben Sie die Bewegung des 6-Achsen-Arms in Worten. Zeichnen Sie, was Ihrer Meinung nach der Stift auf dem 6-Achsen-Arm zeichnen wird.
Sehen Sie sich dieses Video an, um dieses Projekt in Aktion zu sehen. Beobachten Sie das Verhalten des 6-Achsen-Arms.
Entspricht die tatsächliche Bewegung des 6-Achsen-Arms Ihrer Vorhersage? Warum oder warum nicht?
Zeichnet der Stift etwas Ähnliches oder anderes als das, was Sie in Ihrem technischen Notizbuch gezeichnet haben? Wenn es anders ist, warum denken Sie, dass das so ist?

Identifizieren der Bewegungen im Projekt
Lassen Sie uns nun die Verhaltensweisen aufschlüsseln, die Sie in Bezug darauf beobachtet haben, wie sich der 6-Achsen-Arm entlang der x- und y-Achse bewegt. Die ersten beiden Bewegungen ähneln der Art und Weise, wie Sie den 6-Achsen-Arm um Hindernisse herum navigiert haben, während die dritte Bewegung anders ist.
Um die erste Seite des Dreiecks zu zeichnen, bewegt sich der 6-Achsen-Arm entlang der x-Achse.
Wenn wir uns die Koordinaten im Projekt ansehen, beginnt der 6-Achsen-Arm bei (100, 100, 0) und bewegt sich zu (200, 100, 0). Nur die x-Koordinate ändert sich, was auf eine Bewegung entlang der x-Achse hinweist.

Um die zweite Seite des Dreiecks zu zeichnen, bewegt sich der 6-Achsen-Arm entlang der y-Achse.
Betrachtet man die Koordinaten im Projekt erneut, beginnt der 6-Achsen-Arm diese Linie bei (200, 100, 0) und bewegt sich zu (200, 150, 0). Jetzt ändert sich nur noch die y-Koordinate, was auf eine Bewegung entlang der y-Achse hinweist.

Um die dritte Seite des Dreiecks zu zeichnen, bewegt sich der 6-Achsen-Arm in einer diagonalen Linie. Es bewegt sich sowohl entlang der x- als auch der y-Achse, um zur Startkoordinate des Dreiecks zurückzukehren.
Anhand der Koordinaten im Projekt können wir sehen, dass der 6-Achsen-Arm diese letzte Zeile bei (200, 150, 0) beginnt und zu (100, 100, 0) wechselt. Jetzt ändern sich sowohl die x- als auch die y-Koordinaten, was auf eine Bewegung entlang beider Achsen zur gleichen Zeit hinweist.

Mit der Monitorkonsole können Sie sehen, wie sich die x- und y-Werte nacheinander für die beiden Seiten des Dreiecks und dann beide gleichzeitig für die dritte Seite ändern.
In der nächsten Lektion erfahren Sie, wie Sie ein Projekt zum Codieren des 6-Achsen-Arms erstellen, um ein Dreieck für sich selbst zu zeichnen.
Überprüfe dein Verständnis
Bevor Sie mit der nächsten Lektion fortfahren, stellen Sie sicher, dass Sie die Konzepte in dieser Lektion verstehen, indem Sie die Fragen im folgenden Dokument in Ihrem technischen Notizbuch beantworten.
Fragen zum Verständnis prüfen > (Google Doc / .docx / .pdf)
Wählen Sie Weiter > , um zu erfahren, wie Sie dieses Projekt selbst erstellen können.