Skip to main content
Lehrerportal

Berechnung von zwei Übersetzungsverhältnissen

Lehrer-Toolbox-Symbol Lehrer-Toolbox - Der Zweck dieses Abschnitts

Der Zweck der Seiten zum Berechnen von Übersetzungsverhältnissen im Abschnitt Überdenken besteht darin, es den Schülern zu ermöglichen, in Gruppen zu arbeiten, um einzelne Übersetzungsverhältnisse zu berechnen und sie dann zu kombinieren, um ein zusammengesetztes Übersetzungsverhältnis zu erhalten. Sobald die Schüler das zusammengesetzte Übersetzungsverhältnis erhalten haben, bestimmen sie dann den entsprechenden mechanischen Vorteil, der sich aus dem Verhältnis ergibt.

Die Studierenden arbeiten in Vierergruppen. Klicken Sie hier (Google Doc / .docx / .pdf), um eine Liste der Gruppenrollen für diesen Abschnitt anzuzeigen.

Gehen Sie zuerst das erste Beispiel mit den Schülern durch, bevor Sie sie bitten, in Gruppen an den Berechnungen zu arbeiten. Es werden insgesamt drei Berechnungen durchgeführt. Auf der ersten Seite (Berechnung von zwei Übersetzungsverhältnissen) müssen Sie Berechnung 1 mit zwei einzelnen Übersetzungsverhältnissen berechnen, während auf der zweiten Seite (Berechnung von drei Übersetzungsverhältnissen) Berechnung 2 und 3 mit drei einzelnen Übersetzungsverhältnissen berechnet werden müssen.

Ermutigen Sie die Schüler, in ihrer Gruppe zu arbeiten und bei Bedarf Fragen zu stellen.

Jede Berechnung deckt einen der drei folgenden mechanischen Vorteile ab:

  • Erhöhte Geschwindigkeit: ein Verhältnis, bei dem die erste Zahl kleiner als die zweite ist (der Zähler ist kleiner als der Nenner). Ein Beispiel ist 1:15.

  • Erhöhtes Drehmoment: ein Verhältnis, bei dem die zweite Zahl kleiner als die erste ist (der Nenner ist kleiner als der Zähler). Ein Beispiel ist 15:1.

  • Kraftübertragung: ein Verhältnis von 1: 1 (der Zähler ist derselbe wie der Nenner). Ein Beispiel ist 1:1.

Lehrer-Tipps-Symbol Lehrertipps - Vokabeln

Zähler: der obere Teil eines Bruchs.
Nenner: der untere Teil des Bruchs.

Nachdem Sie nun untersucht haben, was Zahnräder sind und wie sie verwendet werden können, um einen mechanischen Vorteil zu erzielen, berechnen Sie nun verschiedene Übersetzungsverhältnisse und kombinieren sie, um ein zusammengesetztes Übersetzungsverhältnis zu erhalten.

Sie arbeiten in Vierergruppen, um die Übersetzungsverhältnisse zu berechnen und den daraus resultierenden mechanischen Vorteil zu ermitteln.

Ein Beispiel anzeigen

Beginnen Sie mit dem folgenden Beispiel:

Eine Tabelle zeigt die Übersetzungszahl in der ersten Spalte, Berechnungen in der mittleren Spalte und das Übersetzungsverhältnis in der dritten Spalte. In der ersten Zeile wird das Übersetzungsverhältnis 1 mit den Berechnungen für ein 12-Zoll-Antriebszahnrad über ein 36-Zoll-Antriebszahnrad und das Verhältnis von 1:3 angezeigt. In der zweiten Zeile wird das Übersetzungsverhältnis 2 mit den Berechnungen für ein 12T-Antriebszahnrad über ein 60T-Antriebszahnrad und einem Verhältnis von 1:5 angezeigt. In der dritten Zeile wird das Ergebnisverhältnis angezeigt, wobei die Berechnungen für ein Verhältnis von 1 zu 15 1 zu 3 mal 1 zu 5 multiplizieren. Die letzte Zeile lautet Vorteil und die Berechnungen lauten Erhöhte Geschwindigkeit: Das 36-T-Antriebszahnrad dreht sich einmal, damit sich das 12-T-Antriebszahnrad 15-mal dreht.

Im obigen Beispiel bezieht sich die Zeile Resultierendes Übersetzungsverhältnis auf das Berechnen des zusammengesetzten Übersetzungsverhältnisses durch Multiplizieren aller einzelnen Übersetzungsverhältnisse miteinander.

Das Übersetzungsverhältnis 1 weist ein 36-Zahnrad (36-Zahnrad) auf, das ein 12-Zahnrad (12-Zahnrad) antreibt. Betrachtet man die Beziehung ist Driven over Driving ergibt 12 zu 36, was sich auf ein Drittel reduziert. Somit ist das Verhältnis 1:3.

Zeile 1 der vorherigen Tabelle zeigt das Übersetzungsverhältnis 1, wobei die Berechnungen ein Verhältnis von 1 zu 3 ergeben.

Ähnlich wie bei Getriebeübersetzung 2 treibt ein 60-Zoll-Getriebe ein 12-Zoll-Getriebe an. Betrachtet man die Beziehung als Driven over Driving, ergibt sich 12 zu 60, was sich auf ein Fünftel reduziert. Somit ist das Verhältnis 1:5.

Die zweite Zeile aus der obigen Tabelle liest das Übersetzungsverhältnis 2 mit den Berechnungen für ein Verhältnis von 1 zu 5.

Um diese beiden Verhältnisse zu kombinieren, wird die Bruchmultiplikation eingeführt. Ein Drittel mal ein Fünftel ist ein Fünfzehntel. Denken Sie daran, dass Sie bei der Multiplikation von Brüchen direkt im Zähler und Nenner multiplizieren. Somit beträgt das zusammengesetzte Übersetzungsverhältnis 1:15.

Die dritte Zeile der obigen Tabelle lautet Ergebnisverhältnis, wobei die Berechnungen zu einem Verhältnis von 1 zu 15 führen.

Sobald das addierte Übersetzungsverhältnis berechnet ist, kann nun bestimmt werden, was der mechanische Vorteil ist. Der daraus resultierende Vorteil ist eine erhöhte Geschwindigkeit: Der 36-Zoll-Antriebs- (Eingangs-) Gang dreht sich einmal, damit sich der 12-Zoll-Antriebs- (Ausgangs-) Gang 15 Mal dreht.

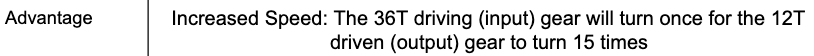
Die vierte Zeile der obigen Tabelle, in der der Vorteil angegeben ist, ist eine erhöhte Geschwindigkeit.

Berechnung 1

Füllen Sie die fehlenden Berechnungen aus der Tabelle Übersetzungsverhältnis aus. Denken Sie daran, dass jede Person entsprechend ihrer Rolle kalkulieren sollte.

Tabelle zur Berechnung von Übersetzungsverhältnissen mit fehlenden Werten. Das Übersetzungsverhältnis 1 zeigt 36T auf dem angetriebenen Zahnrad und 12T auf dem Antriebszahnrad, wobei andere Werte leer sind. Das Übersetzungsverhältnis 2 zeigt ein angetriebenes Zahnrad mit 60 Zähnen und ein Antriebszahnrad mit 12 Zähnen, wobei andere Werte leer sind. Das resultierende Verhältnis und die Art der Vorteilswerte sind ebenfalls leer.

  • Rolle 1: Berechnen Sie das Übersetzungsverhältnis 1 Zeile der obigen Tabelle. Zeigen Sie alle Arbeiten in Ihrem technischen Notizbuch an.
  • Rolle 2: Berechnen Sie die Zeile Übersetzungsverhältnis 2 der obigen Tabelle. Zeigen Sie alle Arbeiten in Ihrem technischen Notizbuch an.
  • Rolle 3: Berechnen Sie die Zeile Ergebnisverhältnis der obigen Tabelle. Überprüfen Sie die Berechnungen aus dem Übersetzungsverhältnis 1 und 2, bevor Sie das endgültige zusammengesetzte Übersetzungsverhältnis berechnen. Zeigen Sie alle Arbeiten in Ihrem technischen Notizbuch an.
  • Rolle 4: Berechnen Sie die Vorteilszeile der obigen Tabelle. Zeigen Sie alle Arbeiten in Ihrem technischen Notizbuch an.
  • Alle Rollen: Sobald die Tabelle abgeschlossen ist, überprüfen Sie mit allen Gruppenmitgliedern, ob die Berechnungen korrekt sind.

Lehrer-Toolbox-Symbol Lehrer-Toolbox - Lösung

Es wird die folgende Lösungstabelle für die Berechnung 1 bereitgestellt. Beachten Sie, dass Calculate 1 das Gegenteil des ersten angegebenen Beispiels ist. Anstelle des zusammengesetzten Übersetzungsverhältnisses von 1:15 beträgt das zusammengesetzte Übersetzungsverhältnis 15:1. Zeigen Sie den Schülern dieses Muster, wenn Sie die Lösung durchgehen. Nennen Sie

ferner die mathematische Begründung für den Unterschied zwischen Drehzahl und Drehmoment, um sicherzustellen, dass die Schüler das Konzept verstehen, da dies in der Lehrer-Toolbox für mechanischen Vorteil auf der folgenden Seite weiter behandelt wird.

Lösungen zeigen das Übersetzungsverhältnis 1 als 3 zu 1, das Übersetzungsverhältnis 2 als 5 zu 1. Die resultierenden Verhältnisberechnungen sind 3 über 1 mal 5 über 1 = 15 über 1 für ein Verhältnis von 15 zu 1. Der Vorteil ist ein erhöhtes Drehmoment, da sich der 12T-Gang 15 Mal dreht, damit sich der 6T-Gang einmal dreht.

Motivations-Diskussionssymbol Diskussion motivieren

F: Welche Operation wird bei der Berechnung des Übersetzungsverhältnisses verwendet?
A: Multiplikation. Wenn Sie Brüche multiplizieren, multiplizieren Sie über den Zähler und Nenner.

F: Was bedeutet der mechanische Vorteil eines erhöhten Drehmoments für einen Roboter im Wettbewerb?
A: Die Antworten können variieren, aber ein Beispiel könnte beinhalten, dass ein Roboter schwere Gegenstände hebt oder trägt.

<  Zurück Zurück Zurück zu Labors Weiter  >