การคำนวณอัตราส่วนเกียร์สอง
กล่องเครื่องมือครู
-
วัตถุประสงค์ของส่วนนี้
วัตถุประสงค์ของหน้าการคำนวณอัตราส่วนเกียร์ในส่วนการคิดใหม่คือเพื่อให้นักเรียนทำงานเป็นกลุ่มเพื่อคำนวณอัตราส่วนเกียร์แต่ละตัวแล้วรวมเข้าด้วยกันเพื่อให้ได้อัตราส่วนเกียร์แบบผสม เมื่อนักเรียนได้อัตราส่วนเกียร์ทบต้นแล้วพวกเขาจะกำหนดความได้เปรียบทางกลที่เหมาะสมซึ่งเป็นผลมาจากอัตราส่วน
นักเรียนจะทำงานเป็นกลุ่มกลุ่มละ 4 คน คลิก ที่นี่ ( Google Doc /.docx /.pdf) เพื่อดูรายการบทบาทกลุ่มสำหรับส่วนนี้
เดินผ่านตัวอย่างแรกกับนักเรียนก่อนที่จะขอให้พวกเขาทำงานเป็นกลุ่มในการคำนวณ จะมีการคำนวณทั้งหมดสามครั้ง หน้าแรก (การคำนวณอัตราส่วนเกียร์สอง) จะมีการคำนวณ 1 โดยมีอัตราส่วนเกียร์สองตัวเพื่อคำนวณในขณะที่หน้าที่สอง (การคำนวณอัตราส่วนเกียร์สาม) จะมีการคำนวณ 2 และ 3 โดยมีอัตราส่วนเกียร์สามตัวเพื่อคำนวณ
กระตุ้นให้นักเรียนทำงานภายในกลุ่มและถามคำถามตามความจำเป็น
การคำนวณแต่ละครั้งจะครอบคลุมหนึ่งในสามข้อได้เปรียบทางกลต่อไปนี้:
-
ความเร็วที่เพิ่มขึ้น: อัตราส่วนที่ตัวเลขตัวแรกน้อยกว่าตัวที่สอง (ตัวเศษน้อยกว่าตัวส่วน) ตัวอย่างคือ 1:15
-
แรงบิดที่เพิ่มขึ้น: อัตราส่วนที่จำนวนที่สองน้อยกว่าจำนวนแรก (ตัวส่วนน้อยกว่าตัวเศษ) ตัวอย่างคือ 15: 1
-
การถ่ายโอนพลังงาน: อัตราส่วน 1 -1 (ตัวเศษเหมือนกันกับตัวส่วน) ตัวอย่างคือ 1: 1
เคล็ดลับสำหรับครู
-
คำศัพท์
ตัว นับ: ส่วนบนของเศษส่วน
ตัว ส่วน: ส่วนล่างของเศษส่วน
ตอนนี้คุณได้สำรวจแล้วว่าเกียร์คืออะไรและสามารถใช้เพื่อสร้างความได้เปรียบทางกลได้อย่างไรตอนนี้คุณจะคำนวณอัตราส่วนเกียร์ที่แตกต่างกันและรวมเข้าด้วยกันเพื่อให้ได้อัตราส่วนเกียร์ผสม
คุณจะทำงานเป็นกลุ่มกลุ่มละ 4 คนเพื่อคำนวณอัตราส่วนเกียร์และกำหนดความได้เปรียบทางกลที่เกิดขึ้น
ดูตัวอย่าง
เริ่มต้นด้วยการดูตัวอย่างต่อไปนี้:
ในตัวอย่างข้างต้นแถวอัตราส่วนผลลัพธ์อ้างอิงถึงการคำนวณอัตราส่วนเกียร์ของ สารประกอบ โดยการคูณอัตราส่วนเกียร์แต่ละตัวทั้งหมดเข้าด้วยกัน
อัตราทดเกียร์ 1 มีเฟือง 36 ฟัน (เฟือง 36T) ขับเฟือง 12 ฟัน (เฟือง 12T) การดูความสัมพันธ์เป็นตัวขับเคลื่อนมากกว่าผลการขับขี่ใน 12 มากกว่า 36 ซึ่งลดลงเหลือหนึ่งในสาม ดังนั้นอัตราส่วนคือ 1: 3
ในทำนองเดียวกันสำหรับอัตราทดเกียร์ 2 เกียร์ 60T กำลังขับเกียร์ 12T การมองความสัมพันธ์เป็นแรงผลักดันต่อการขับขี่ส่งผลให้เกิด 12 มากกว่า 60 ซึ่งลดลงเหลือ 1 ใน 5 ดังนั้นอัตราส่วนคือ 1: 5
ในการรวมอัตราส่วนทั้งสองเข้าด้วยกันการคูณเศษส่วนถูกนำเข้ามา หนึ่งในสามคูณหนึ่งในห้าได้หนึ่งในสิบห้า โปรดจำไว้ว่าเมื่อคูณเศษส่วนคุณจะคูณตรงข้ามทั้งตัวเศษและตัวส่วน ดังนั้น, อัตราส่วนเฟืองของสารประกอบคือ 1:15
เมื่อคำนวณอัตราส่วนเกียร์แบบทบต้นแล้วตอนนี้สามารถกำหนดได้ว่าข้อได้เปรียบทางกลคืออะไร ข้อได้เปรียบที่ได้คือความเร็วที่เพิ่มขึ้น: เฟืองขับ (อินพุต) 36T จะหมุนหนึ่งครั้งเพื่อให้เฟืองขับ (เอาต์พุต) 12T หมุน 15 ครั้ง
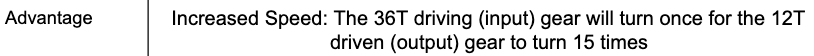
การคำนวณ 1
กรอกข้อมูลการคำนวณที่ขาดหายไปจากตารางอัตราส่วนเกียร์ โปรดทราบว่าแต่ละคนควรคำนวณตามบทบาทของตนเอง
- บทบาทที่ 1: คำนวณอัตราส่วนเกียร์ 1 แถวของตารางข้างต้น แสดงผลงานทั้งหมดในสมุดบันทึกวิศวกรรมของคุณ
- บทบาทที่ 2: คำนวณอัตราส่วนเกียร์ 2 แถวของตารางข้างต้น แสดงผลงานทั้งหมดในสมุดบันทึกวิศวกรรมของคุณ
- บทบาทที่ 3: คำนวณแถวอัตราส่วนผลลัพธ์ของตารางข้างต้น ตรวจสอบการคำนวณจากอัตราส่วนเกียร์ 1 และ 2 ก่อนที่จะคำนวณอัตราส่วนเกียร์สารประกอบสุดท้าย แสดงผลงานทั้งหมดในสมุดบันทึกวิศวกรรมของคุณ
- บทบาทที่ 4: คำนวณแถว Advantage ของตารางข้างต้น แสดงผลงานทั้งหมดในสมุดบันทึกวิศวกรรมของคุณ
- บทบาททั้งหมด: เมื่อตารางเสร็จสมบูรณ์ให้ตรวจสอบกับสมาชิกในกลุ่มทั้งหมดว่าการคำนวณถูกต้อง
กล่องเครื่องมือครู
- การ
แก้ปัญหา
สิ่งที่มีให้คือตารางคำตอบต่อไปนี้สำหรับการคำนวณ 1 สังเกตว่าคำนวณ 1 เป็นตัวผกผันกับตัวอย่างแรกที่ให้ไว้ แทนที่อัตราส่วนเฟืองของสารประกอบคือ 1:15, อัตราส่วนเฟืองของสารประกอบคือ 15: 1 ชี้ให้นักเรียนเห็นรูปแบบนี้เมื่อพูดถึงคำตอบ
นอกจากนี้ให้เรียกการให้เหตุผลทางคณิตศาสตร์สำหรับความแตกต่างระหว่างความเร็วและแรงบิดเพื่อให้แน่ใจว่านักเรียนเข้าใจแนวคิดเนื่องจากจะมีการกล่าวถึงต่อไปในกล่องเครื่องมือของครูสำหรับข้อได้เปรียบทางกลในหน้าต่อไป
สร้างแรงจูงใจในการอภิปราย
ถาม: การดำเนินการใดที่ใช้ในการคำนวณอัตราส่วนเฟืองผสม
ตอบ: การคูณ เมื่อคูณเศษส่วนให้คูณข้ามตัวเศษและตัวส่วน
ถาม: ข้อได้เปรียบทางกลของแรงบิดที่เพิ่มขึ้นมีความหมายอย่างไรสำหรับหุ่นยนต์ในการแข่งขัน
ตอบ: คำตอบอาจแตกต่างกันไปแต่ตัวอย่างอาจรวมถึงหุ่นยนต์ยกหรือบรรทุกของหนัก